39. 组合总和

难度：medium

类型：回溯

思路：

这道题的特点是，组合没有元素个数要求，数组无重复元素，每个元素可以无限选取。

组合没有元素个数要求：不需要通过path长度判断来跳出递归，通过sum来跳出；

数组无重复元素：不需要进行去重操作

每个元素可以无限选取：每次进行下层递归时，startIndex为i，不是i+1

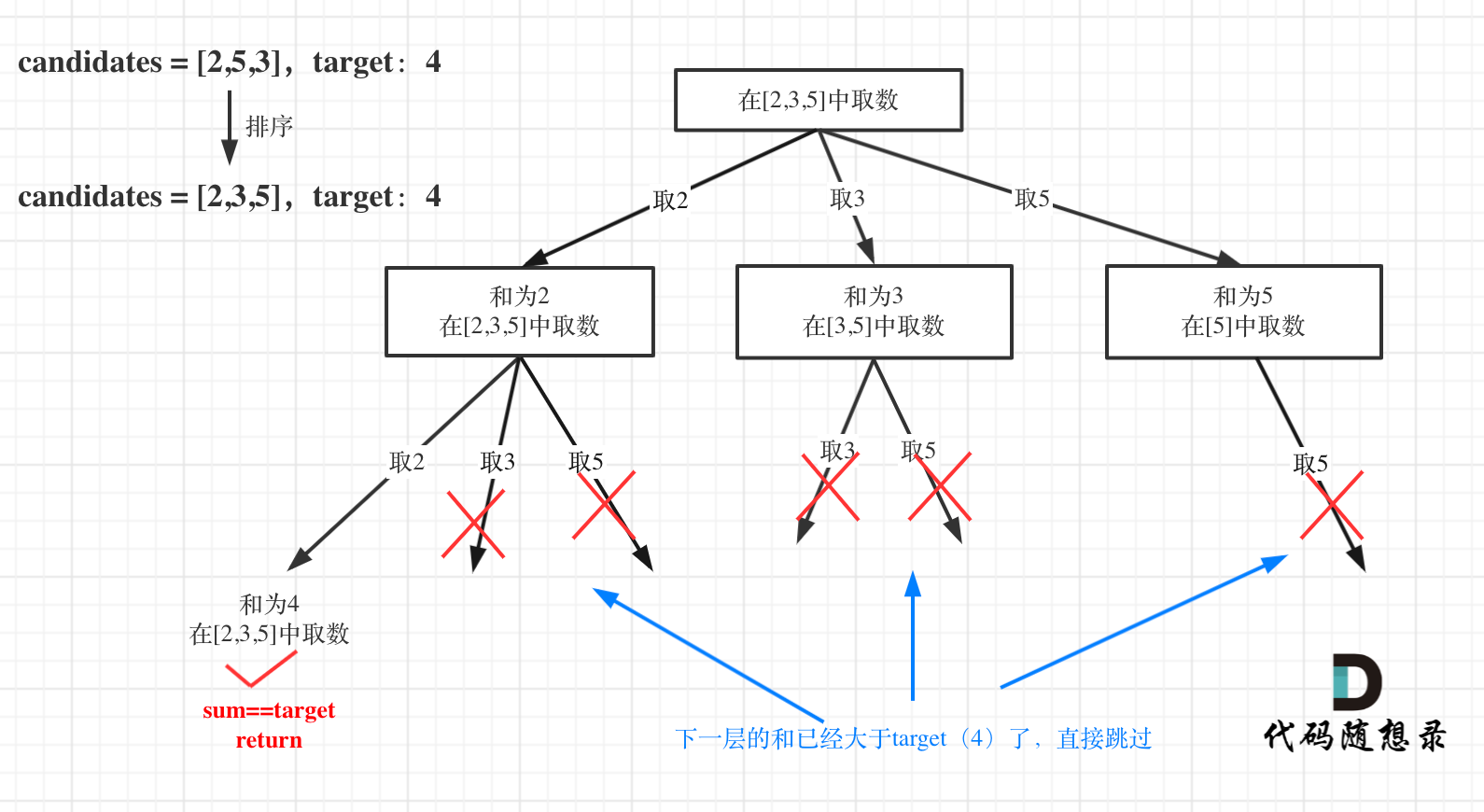
39.组合总和1

先给数组排序，是为了后续的剪枝操作；

代码：

class Solution {private List<Integer> path = new ArrayList<>();private List<List<Integer>> ans = new ArrayList<>();private int sum = 0;public List<List<Integer>> combinationSum(int[] candidates, int target) {     if (candidates.length == 0) {return ans;} // 排序Arrays.sort(candidates);backtracking(candidates, target, 0);return ans;}public void backtracking(int[] candidates, int target, int startIndex) {// if (sum > target) {//     return;// }if (sum == target) {ans.add(new ArrayList<>(path));return;}// 剪枝操作：sum + candidates[i] <= target，若超过target，不需要进入下一层递归判断for (int i = startIndex; i < candidates.length; i++) {if (sum + candidates[i] > target) {break;}sum += candidates[i];path.add(candidates[i]);backtracking(candidates, target, i);sum -= candidates[i];path.remove(path.size() - 1);}}}

时间复杂度: O(n * 2^n)，注意这只是复杂度的上界，因为剪枝的存在，真实的时间复杂度远小于此
空间复杂度: O(target)

40. 组合总和 II

难度：medium

类型：回溯

思路：

本题的特点是：集合中有重复元素，集合每个元素在每个组合只能使用一次；

集合中有重复元素：进行去重操作；避免递归树中同一层有重复元素，同一层的元素会出现在path的相同位置，会造成重复的组合（去重前先要排序）

1.使用startIndex方法去重

i>0无法确定candidates[i]和candidates[i - 1]是同层还是同枝；而i>startIndex可以确定是同层;

            if (i > startIndex && candidates[i] == candidates[i - 1]) {continue;

2.使用used数组去重

           if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}

· 在candidates[i] == candidates[i - 1]相同的情况下：

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

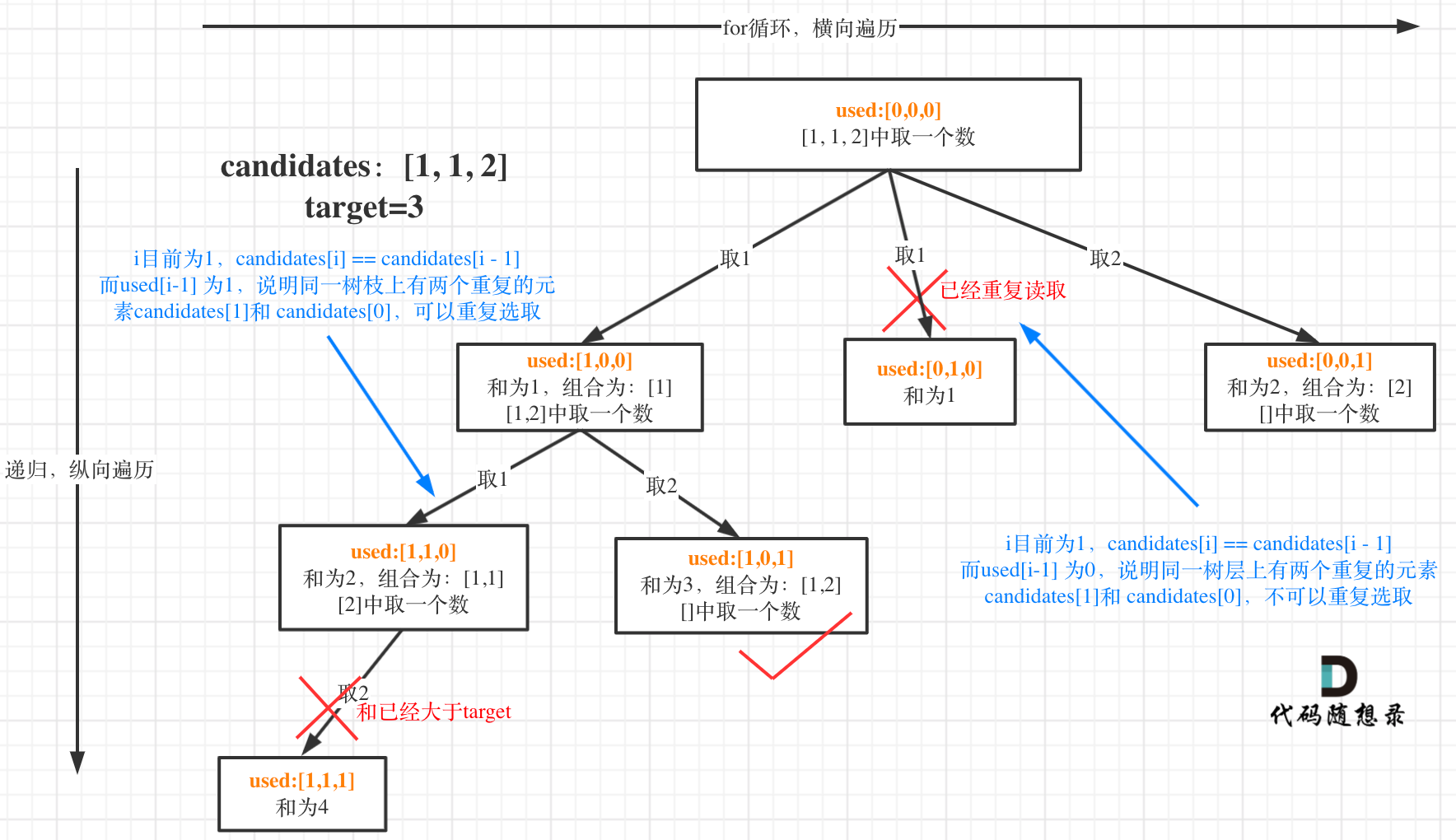
40.组合总和II1

集合每个元素在每个组合只能使用一次：调用递归时，startIndex为i+1

代码：

class Solution {private List<List<Integer>> ans = new ArrayList<>();private List<Integer> path = new ArrayList<>();private int sum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {if (candidates.length == 0) {return ans;}Arrays.sort(candidates);backtracking(candidates, target, 0);return ans;}public void backtracking(int[] candidates, int target, int startIndex) {if (sum == target) {ans.add(new ArrayList<>(path));return;}for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {// 避免递归树中同一层有重复元素，同一层的元素会出现在path的相同位置，会造成重复的组合// 例如candidates = [1,2,2,2,2,3,3,3,3]，target = 6if (i > startIndex && candidates[i] == candidates[i - 1]) {continue;}sum += candidates[i];path.add(candidates[i]);backtracking(candidates, target, i + 1);sum -= candidates[i];path.remove(path.size() - 1);}}
}// 使用used数组方法
class Solution {private List<List<Integer>> ans = new ArrayList<>();private List<Integer> path = new ArrayList<>();private boolean[] used;// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过// used[i - 1] == false，说明同一树层candidates[i - 1]使用过private int sum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {if (candidates.length == 0) {return ans;}Arrays.sort(candidates);used = new boolean[candidates.length];backtracking(candidates, target, 0);return ans;}public void backtracking(int[] candidates, int target, int startIndex) {if (sum == target) {ans.add(new ArrayList<>(path));return;}for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {// 这里是关键区别，除了对used[i-1]判定外，i>0也不同于上面的i>startIndex// 因为i>0无法确定candidates[i]和candidates[i - 1]是同层还是同枝；而i>startIndex可以确定是同层if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.add(candidates[i]);used[i] = true;backtracking(candidates, target, i + 1);sum -= candidates[i];path.remove(path.size() - 1);used[i] = false;}}
}

时间复杂度: O(n * 2^n)
空间复杂度: O(n)

131. 分割回文串

难度：medium

类型：回溯

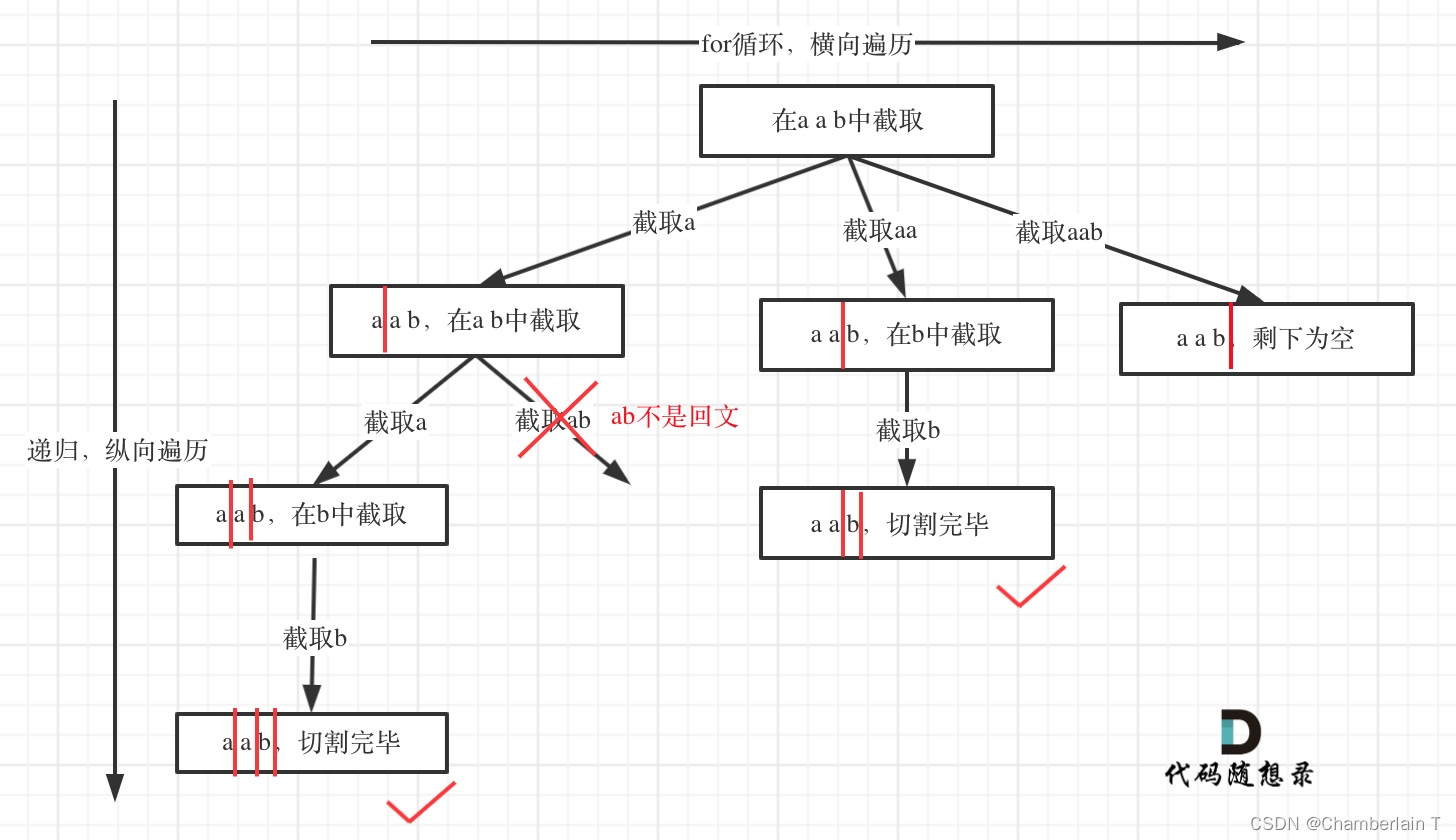
思路：

本题为切割问题，也是组合的一种。

131.分割回文串

代码：

class Solution {private List<List<String>> ans = new ArrayList<>();private List<String> path = new ArrayList<>();public List<List<String>> partition(String s) {backtracking(s, 0);return ans;}public void backtracking(String s, int startIndex) {if (startIndex == s.length()) {ans.add(new ArrayList<>(path));return;}for (int i = startIndex; i < s.length(); i++) {// substring()方法为左闭右开String str = s.substring(startIndex, i + 1);if (judge(str)) {path.add(str);backtracking(s, i + 1);path.remove(path.size() - 1);}}}public boolean judge(String s) {int left = 0; int right = s.length() - 1;while (left < right) {if (s.charAt(left) != s.charAt(right)) {return false;}left++;right--;}return true;}
}

时间复杂度: O(n * 2^n)
空间复杂度: O(n^2)