目录
力扣494. 目标和
问题解析
解析代码
滚动数组优化代码
力扣494. 目标和
494. 目标和
难度 中等
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {}
};问题解析
本题可以直接用暴搜的方法解决。但是稍微用数学知识分析⼀下,就能转化成常见的背包模型问题。
设我们最终选取的结果中,前面加 + 号的数字之和为 a ,前面加 - 号的数字之和为 b ,整个数组的总和为 sum ,于是有:
- a + b = sum
- a - b = target
上面两个式子消去 b 之后,可以得到 a = (sum + target) / 2 ,也就是说,我们仅需在 nums 数组中选择一些数,将它们凑成和为 (sum + target) / 2 即可。问题就变成了力扣416. 分割等和子集这道题。 可以用相同的分析模式,来处理这道题。
以某个位置为结尾,结合题目要求,定义一个状态表示:
dp[i][j] 表示:在前 i 个数中选,总和正好等于 j ,一共有多少种选法。
状态转移方程:
dp 状态转移方程分析方式,一般都是根据最后一步的状况,来分情况讨论:
- 不选择 nums[i] :那么我们凑成总和 j 的总方案,就要看在前 i - 1 个元素中选,凑成总和为 j 的方案数。根据状态表示,此时 dp[i][j] = dp[i - 1][j] ; 。
- 选择 nums[i] :这种情况下是有前提条件的,此时的 j 应该是大于等于 nums[i]。 因为如果这个元素都比要凑成的总和大,那选择它就没有意义。那么能够凑成总和为 j 的方案数,就要看在前 i - 1 个元素中选,能否凑成总和为 j - nums[i] 。根据 状态表示,此时 dp[i][j] = dp[i - 1][j - nums[i]] ; (j >= nums[i] )。
综上,两种情况如果存在的话,应该要累加在⼀起。因此,状态转移方程为: if(j >= nums[i - 1]) dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]] ; else dp[i][j] = dp[i - 1][j] ;(如果多加一行一列,找原数组下标要减1)
初始化:多加一行一列,方便初始化,由于需要用到上一行的数据,因此可以先把第一行初始化。 第一行表示不选择任何元素,要凑成目标和 j 。只有当目标和为 0 的时候才能做到,因此第一行仅需初始化第一个元素 dp[0][0] = 1。
填表顺序:根据状态转移方程,需要从上往下填写每一行,每一个的顺序是任意的。
返回值:根据状态表示,返回 dp[n][a] 的值。 其中 n 表示数组的大小, target 表示要凑成的目标和。
解析代码
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0, n = nums.size();;for(auto& e : nums){sum += e;}int a = (sum + target) / 2;if(a < 0 || (sum + target) % 2) // 小于0或者除不尽return 0;vector<vector<int>> dp(n + 1, vector<int>(a + 1, 0));dp[0][0] = 1;for(int i = 1; i <= n; ++i){for(int j = 0; j <= a; ++j) // 第1列用到dp[0][0]初始化{if(j >= nums[i - 1])dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];elsedp[i][j] = dp[i - 1][j];}}return dp[n][a];}
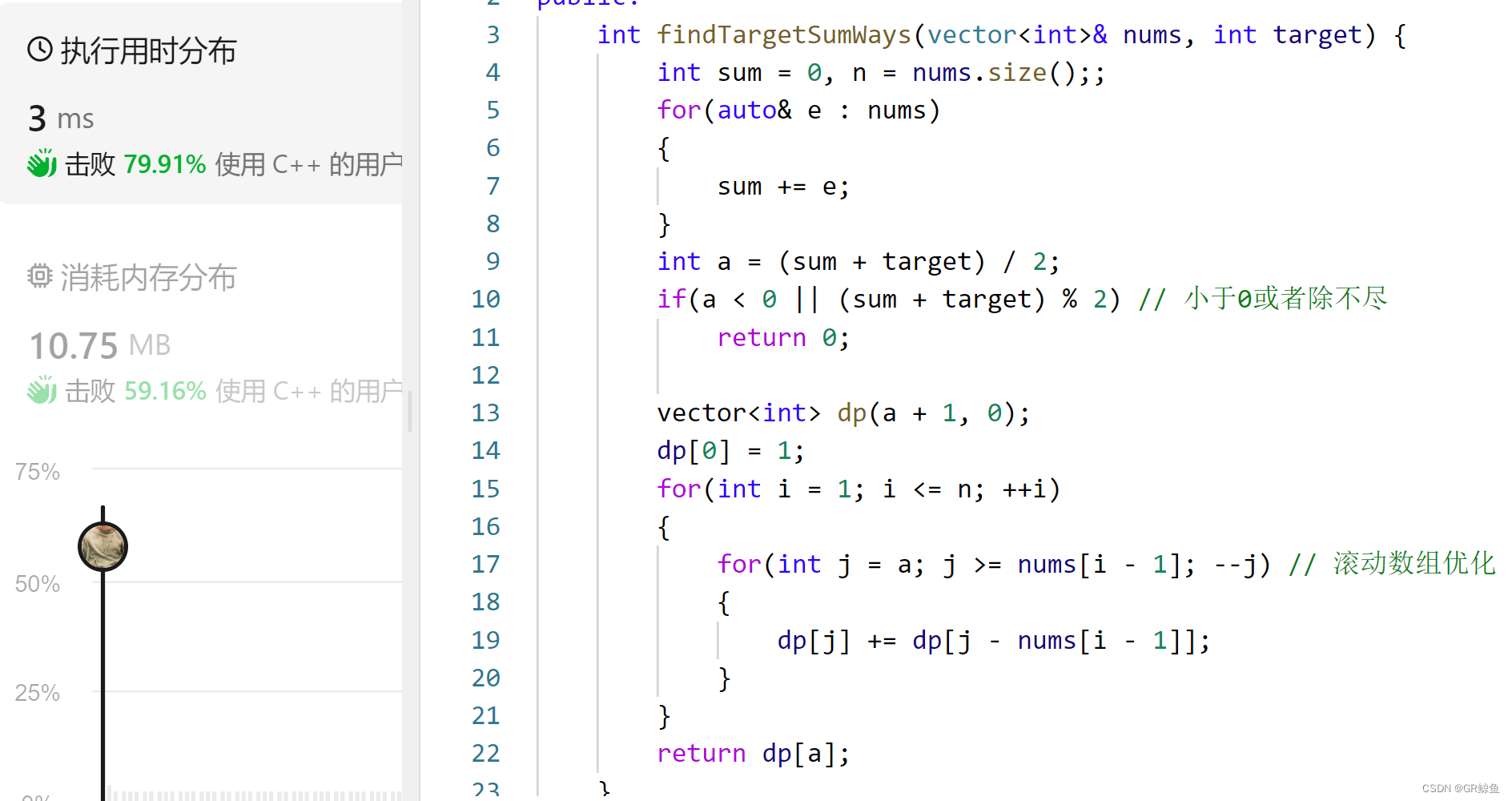
};滚动数组优化代码
背包问题基本上都是利用滚动数组来做空间上的优化:(时间也有常数的优化)
- 利用滚动数组优化。
- 直接在原始代码上修改。
在01背包问题中,优化的结果为:
- 删掉所有的横坐标。
- 修改一下 j 的遍历顺序。
(滚动数组优化代码只需能在原代码上修改就行,不用考虑什么状态表示)
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0, n = nums.size();;for(auto& e : nums){sum += e;}int a = (sum + target) / 2;if(a < 0 || (sum + target) % 2) // 小于0或者除不尽return 0;vector<int> dp(a + 1, 0);dp[0] = 1;for(int i = 1; i <= n; ++i){for(int j = a; j >= nums[i - 1]; --j) // 滚动数组优化{dp[j] += dp[j - nums[i - 1]];}}return dp[a];}
};