【学习心得】神经网络知识中的符号解释②-编程知识

【学习心得】神经网络知识中的符号解释②

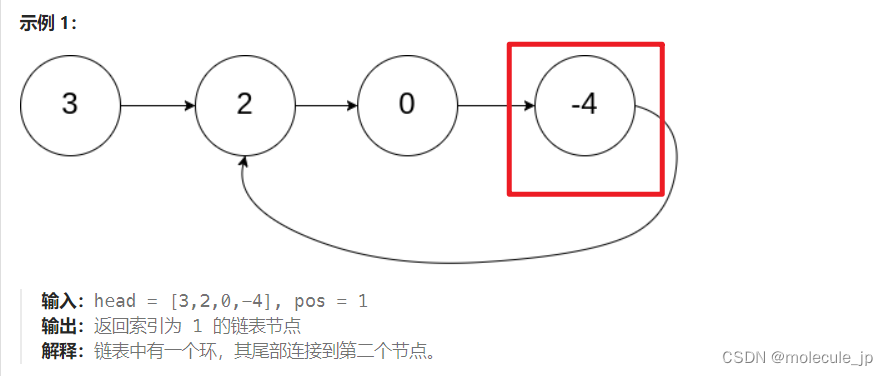
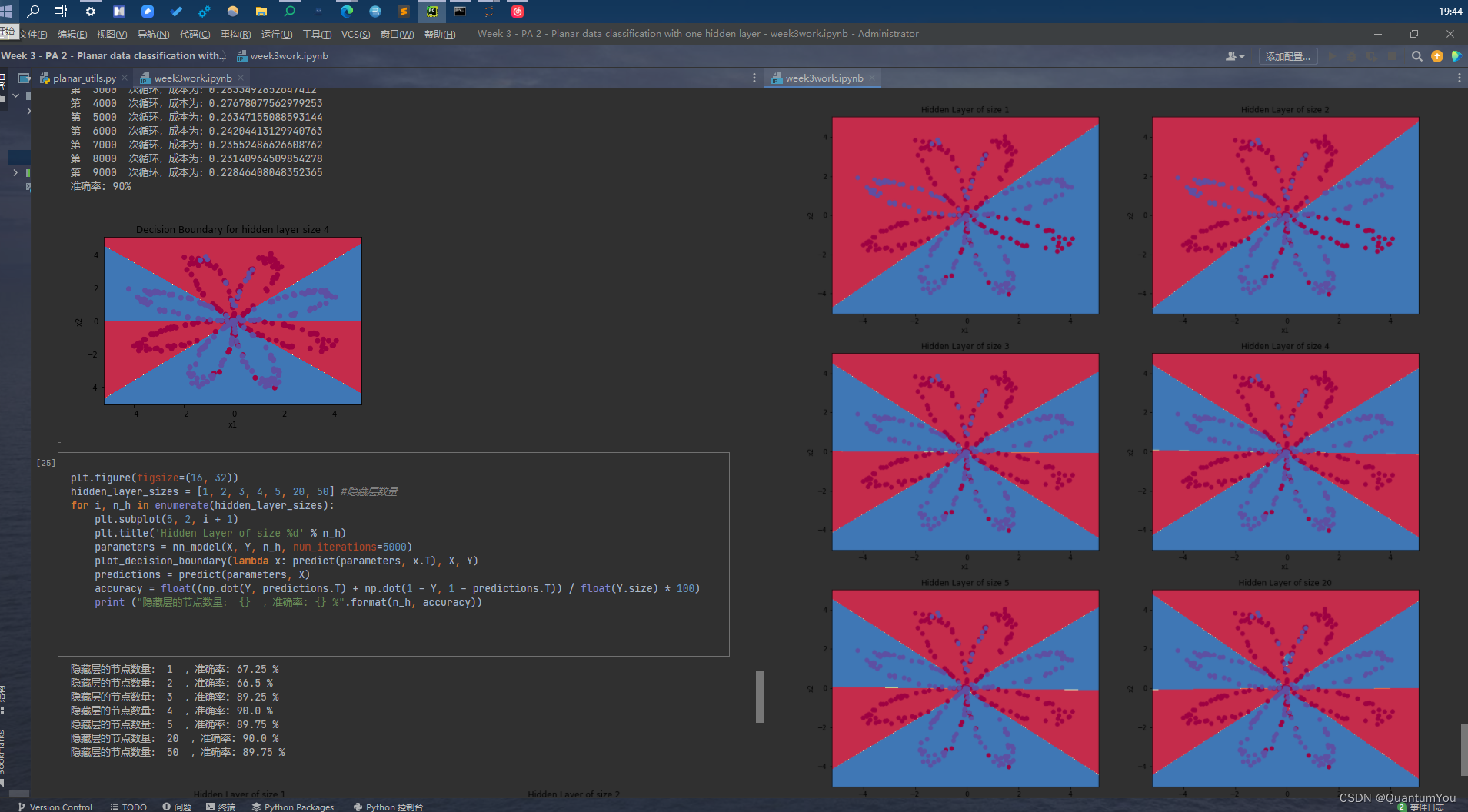
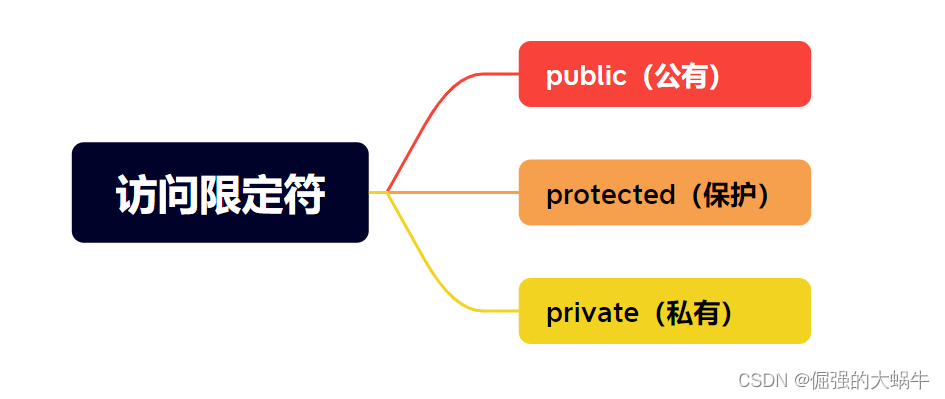
我在上篇文章中初步介绍了一些神经网络中的符号，只有统一符号及其对应的含义才能使我自己在后续的深度学习中有着一脉相承的体系。如果对我之前的文章感兴趣可以点击链接看看哦：

【学习心得】神经网络知识中的符号解释①http://t.csdnimg.cn/f6PeJ

一、神经网络简单模型

今天我以逻辑回归任务为例来介绍更多神经网络中的符号和他们对应的概念解释。先看一个超简单的神经网络模型：

这个模型对应了一个公式：

$\left.\begin{matrix} x\\ w\\ b \end{matrix}\right\}\Rightarrow z=w^Tx+b$

x是你输入的特征。w是权重，b是偏置，他们统称参数。我们可以将逻辑回归的模型再精细一点：

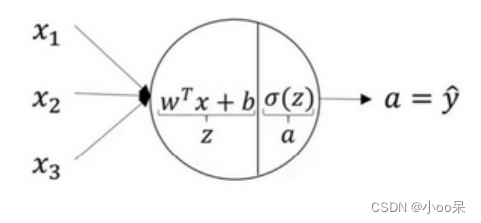
可见中间这个点，其实是有两个部分组成，第一个部分是线性部分，第二个部分是非线性部分。z是线性回归部分的输出，a是激活函数的输出。他们合在一起组成了逻辑回归的输出 $\hat y$ 。可以写成如下公式：

$\left.\begin{matrix} x\\ w\\ b \end{matrix}\right\}\Rightarrow z=w^Tx+b\Rightarrow a=\sigma (z)\Rightarrow L(a,y)$

公式中的 $\sigma$ 是Sigmoid函数（激活函数的一种），L是损失函数（Loss Function）。好的介绍到这里我来个表格给大家复习一下：

符号	解释
$x$	特征值向量 $x=[x_1,x_2,x_3]^T$
$z$	线性回归方程
$\sigma$	Sigmoid激活函数
$L$	损失函数
$w$	权重向量 $w=[w_1,w_2,w_3]^T$
$b$	偏置，偏置是一个标量在计算的时候被广播

二、两层神经网络

不废话，直接看图：

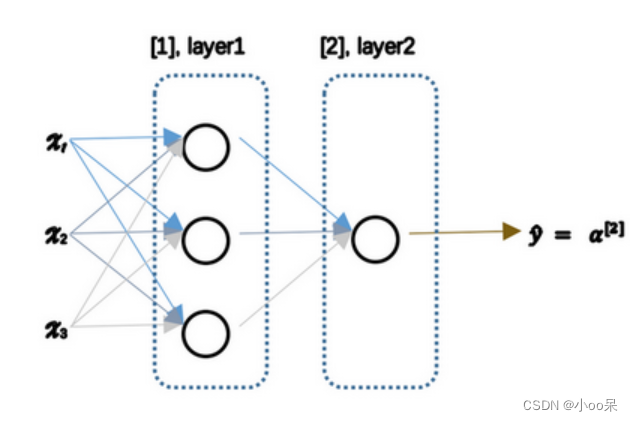
从图中可知，我们有三个输入特征 $x_1,x_2,x_3$ 他们被竖起来堆叠，这叫做神经网络的输入层。中间有两个虚线，其中处最后一个外，统称隐藏层。而最后一个虚线部分（这层只有一个节点）叫做输出层。

我们还用之前的公式和符号来表示这个神经网络模型，但稍有不同：

$\left.\begin{matrix} x\\ W^{[1]}\\ b^{[1]} \end{matrix}\right\}\Rightarrow z^{[1]}=W^{[1]}x+b^{[1]}\Rightarrow a^{[1]}=\sigma (z^{[1]})$

我们使用上角标中括号里面写数字的形式来表示第几层神经网络 $^{[m]}$ 。这里要和之前的小括号里面写数字的形式区分开来 $^{(i)}$ 它表示第i个训练样本。可见上面这个公式只写出了第1层神经网络的公式。接下来我们把第二层也写出来：

$\left.\begin{matrix} a^{[1]}\\ W^{[2]}\\ b^{[2]} \end{matrix}\right\}\Rightarrow z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}\Rightarrow a^{[2]}=\sigma (z^{[2]})\Rightarrow L(a^{[2]},y)$

和上面的第1层比较类似，我就不赘述。上面我介绍了两层神经网络的正向传播，接下来要介绍反向传播的公式：

$\left.\begin{matrix} da^{[1]}=d\sigma(z^{[1]})\\ dW^{[2]}\\ db^{[2]} \end{matrix}\right\}\Leftarrow dz^{[2]}=d(W^{[2]}a^{[1]}+b^{[2]})\Leftarrow da^{[2]}=d\sigma(z^{[2]})$

$\Leftarrow dL(a^{[2]},y)$

这里面要解释的符号，就是da它是每一层逻辑回归输出的梯度，dz它是每一层线性回归输出的梯度，dW是每一层权重的梯度，db是每一层偏置的梯度。

好啦，让我再用一个表格为大家总结一下：

符号	解释
$^{[m]}$	上角标中括号里面写数字，代表第m层
$W$	偏置w的行向量形式，即 $w^T$
$a^{[0]}$	第0层的输出，其实就是输入层的特征值向量x
$da^{[i]}$	第 $i$ 层输出的梯度
$dz^{[i]}$	第 $i$ 层线性回归输出的梯度
$dW^{[i]}$	第 $i$ 层权重的梯度
$db^{[i]}$	第 $i$ 层偏置的梯度