相机参数的意义-编程知识

相机标定的意义：

相机标定：使用带有pattern的标定板来求解相机参数的过程；
用一个简化的数学模型来代表复杂的三维到二维的成像过程；
相机参数包括：相机内参（焦距等），外参（旋转矩阵等），镜头畸变参数
用途：畸变矫正，双目视觉，结构光，三维重建，SLAM等

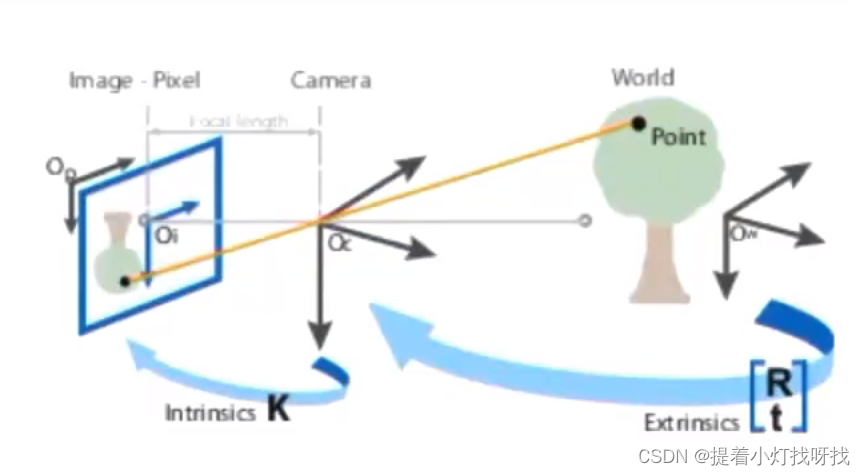
世界坐标系（World Coords）：点在真实世界中的位置，描述相机的位置，单位为m；
相机坐标系（Camera Coords）：以相机sensor中心为原点，建立相机坐标系，单位m；
图像物理坐标系：经过小孔成像后得到的二维坐标系，单位是mm，坐标原点是图中的点c；
像素坐标系（Pixcel Coords）：成像点在相机sensor上像素的行数和列数，不带有任何的物理单位
主点：光轴与图像平面的交点为主点，图中的点p。

1、世界坐标系到相机坐标系的转换

点p在不同坐标系的表示：

世界坐标系： $P(x_{w},y_{w},z_{w})$ ;
相机坐标系： $P(x_{c},y_{c},z_{c})$

坐标系之间的转换：

R：相机坐标系对于世界坐标系的旋转矩阵；
T：相机坐标系对于世界坐标系的平邑矩阵。

转换关系：

$\begin{bmatrix} x_{c}\\ y_{c}\\ z_{c}\\ 1 \end{bmatrix}=\begin{bmatrix} R_{3\times 3} & T_{3\times 1} \\ 0& 1 \end{bmatrix}\cdot \begin{bmatrix} x_{w}\\ y_{w}\\ z_{w}\\ 1 \end{bmatrix}$

2、相机坐标系到图像坐标系的转换

假设点 $p(x_{c},y_{c},z_{c})$ 在图像坐标系的成像点是 $p{}'(x,y)$ ;
基于小孔成像的原理；
空间中一点成像在平面中，与XOY平面平行，距离原点f的平面；
取一个截面ZOY，可以得到上图，根据相似三角形关系可以计算得到：

$\frac{x}{x_{c}}=\frac{y}{y_{c}}=\frac{f}{z_{c}}$

化简后可以得到：

$x=\frac{f}{z_{c}}\cdot x_{c}$

$y=\frac{f}{z_{c}}\cdot y_{c}$

写为矩阵可得：

$z_{c}\cdot \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}=\begin{bmatrix} f & 0 & 0&0 \\ 0 & f & 0 & 0\\ 0 & 0& 1 & 0 \end{bmatrix}\cdot \begin{bmatrix} x_{c}\\ y_{c}\\ z_{c}\\ 1 \end{bmatrix}$

3、图像坐标系到像素坐标系的转换

坐标系的转换：

图像坐标系的点 $p{}'(x,y)$ 到像素坐标系的 $(u,v)$ 的转换；
图像坐标系的原点在sensor的中央，单位是mm;
像素坐标系的原点在sensor的左上角，单位是Pixel，也就是像素的行数和列数；
转换关系：

$u=\frac{x}{dx}+ u_{0}$

$v=\frac{y}{dy}+ v_{0}$

矩阵表示：

$z_{c}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}=\begin{bmatrix} f & 0 & 0&0 \\ 0 & f & 0 & 0\\ 0 & 0& 1 & 0 \end{bmatrix}\cdot \begin{bmatrix} x_{c}\\ y_{c}\\ z_{c}\\ 1 \end{bmatrix}$

$dx,dy$ ：sensor的固有参数，代表每个像素的毫米数；
$u_{0},v_{0}$ ：代表图像坐标系原点（光心）相对像素坐标系原点的偏移量

综上：相机坐标系到像素坐标系的转换公式：

相机坐标系和世界坐标系重合，不考虑世界坐标系的旋转平移：

$u=f_{x} \ast \frac{x_{c}}{z_{c}}+ u_{0}$

$v=f_{y} \ast \frac{y_{c}}{z_{c}}+ v_{0}$

上式中： $f_{x}=\frac{f}{dx}$ ， $f_{y}=\frac{f}{dy}$ 焦距除以单个像素的大小
相机的标定过程中， $f,dx,dy$ 不能标定得到， $f{_{x}},f_{y}$ 可以通过标定得到

4、完整坐标系转换

世界坐标系到像素坐标系转换：

$z_{c}\cdot \begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} \frac{1}{dx} & 0 & u_{0}\\ 0 & \frac{1}{dy} & v_{0} \\ 0 & 0& 1 \end{bmatrix}\cdot \begin{bmatrix} f & 0 & 0&0 \\ 0 & f & 0 & 0\\ 0 & 0& 1 & 0 \end{bmatrix}\cdot \begin{bmatrix} R_{3\times 3} & T_{3\times 1} \\ 0& 1 \end{bmatrix}\cdot \begin{bmatrix} x_{w}\\ y_{w}\\ z_{w}\\ 1 \end{bmatrix}=M_{1} M_{2} \begin{bmatrix} x_{w}\\ y_{w}\\ z_{w}\\ 1 \end{bmatrix}$

相机内参：相机的焦距，像素坐标系的相对偏移量

$M_{1}=\begin{bmatrix} f_{x} & 0 & u_{0}\\ 0 & f_{y} & v_{0} \\ 0 & 0& 1 \end{bmatrix}$

相机外参：世界坐标系到相机坐标系的转换关系，相机再世界坐标系的位置矩阵

$M_{2}=\begin{bmatrix} R_{3\times 3} & T_{3\times 1} \end{bmatrix}=\begin{bmatrix} r_{11} & r_{12} & r_{13} & t_{1}\\ r_{21} & r_{22} & r_{23} & t_{2}\\ r_{31}& r_{32} & r_{33} & t_{3} \end{bmatrix}$

5、镜头畸变

镜头畸变：

经过透视后的实际成像和理想成像之间的误差即为镜头畸变

主要分为径向畸变和切向畸变

径向畸变

增加的透镜形状造成，沿透镜的径向分布
分为桶形畸变和枕形畸变
远离透镜中心的地方比较靠近中心的地方更加弯曲
光心处的畸变为0，距离光心越远畸变越大
廉价相机，畸变更严重
径向畸变的数学多项式描述：

$\left\{\begin{matrix} x_{distorted}=x(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6})\\ y_{distorted}=y(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6}) \end{matrix}\right.$

$(x,y)$ 是没有畸变的像素点， $(x_{distorted},y_{distorted})$ 畸变后的位置
$k_{1},k_{2},k_{3}$ ：径向畸变系数，摄像头的内参，一般使用前两项，鱼眼相机会使用第三项。

切向畸变：

相机sensor和镜头不平行导致
切向畸变的数学表达式：

$\left\{\begin{matrix} x_{distorted}=x+[2p_{1}xy+p_{2}(r^{2}+2x^{2})]\\ y_{distorted}=y+[2p_{2}xy+p_{1}(r^{2}+2y^{2})] \end{matrix}\right.$

两个畸变合并：

$\left\{\begin{matrix} x_{distorted}=x(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6})+[2p_{1}xy+p_{2}(r^{2}+2x^{2})]\\ y_{distorted}=y(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6})+[2p_{2}xy+p_{1}(r^{2}+2y^{2})] \end{matrix}\right.$

6、平面的单应性关系：

定义：从一个平面到另一个平面的投影映射
世界坐标系的物体平面到成像平面之间的映射，即两个平面之间的单应性关系
模型平面：标定使用的标定板平面
模型平面上的一点： $Q=[X,Y,Z,1]^{T}$ （向量增广为了方便计算）
映射到成像平面上的点： $q=[x,y,1]^T$
它们两者之间的单应性关系： $q=x\cdot H\cdot Q$
$H$ ：单应性矩阵，单应性矩阵有8个自由度，8个自由度参数求解
四个点可以得到8个方程，所以至少四个点就可以求解单应性关系
Opencv接口：fingHomography
求解方法：1.重投影误差最小化；2.RANSAC

基本变量：

二维点： $m=[u,v]^T$ ，对应的三维空间中的点 $M=[X,Y,Z]^T$
增加1得到增广向量： $\widehat{m}=[u,v,1]^T$ , $\widehat{M}=[X,Y,Z,1]^T$
根据前面的模型，三位点到投影点的关系可以描述为： $s\widehat{m}=A[R t]\widehat{M}$
$s$ ：转换尺度因子， $[Rt]$ ：外参，旋转平移矩阵
$A$ ：外参，可以表示为：

$A=\begin{bmatrix} \alpha & \gamma & u_{0}\\ 0 & \beta & v_{0}\\ 0& 0 & 1 \end{bmatrix}$

$(u_{0},v_{0})$ ：代表图像坐标系元代你（光心）相对像素坐标系原点的偏移量
$\alpha ,\beta$ ：焦距除以单个像素的大小，在两个轴的比例因子
$\gamma$ ：两个坐标轴的倾斜角的参数
前面没有提到，因为我们认为两个坐标轴是垂直的，世界可能不垂直
相机标定
我么可以假设，标定板平面在世界坐标系的z坐标是0，R的第 $i$ 列矩阵为 $r_{i}$ ，那么可以得到：

$s\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=A\begin{bmatrix} r_{1} & r_{2} & r_{3} &t \end{bmatrix}\begin{bmatrix} X\\ Y\\ 0\\ 1 \end{bmatrix}=A\begin{bmatrix} r_{1} & r_{2} & t \end{bmatrix}\begin{bmatrix} X\\ Y\\ 1 \end{bmatrix}$

标定平面和成像平面的单应性关系： $s\widehat{m}=H\widehat{M} withH=A\begin{bmatrix} r_{1} & r_{2} & t \end{bmatrix}$
如前所述，可以通过两个平面上的多个点求解单应性矩阵H
假设 $H=[h_1,h_2,h_3]=> \begin{bmatrix} h_1 & h_2 & h_3 \end{bmatrix}=\lambda A\begin{bmatrix} r_1 & r_2 & t \end{bmatrix}$
根据上式可以得到：