题目

t(t<=100)组样例，长为n(n<=2000)的序列

交互题，每次你可以询问一个区间[l,r]的逆序对数，代价是

要在的代价内问出最大元素的位置，输出其位置

思路来源

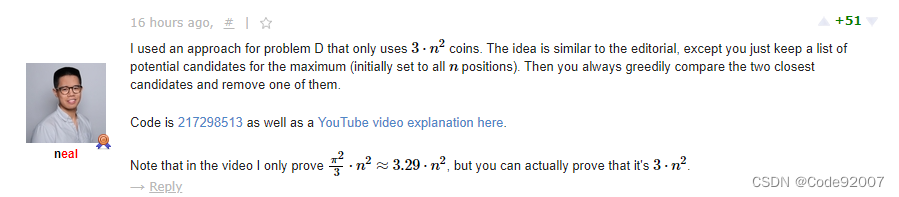
neal

Codeforces Round 890 (Div. 2) supported by Constructor Institute D (交互+分治) 附加强 - 知乎

题解

赛中开题顺序大失败没看这个sb题

赛后用一种不超过的搞过去了，也就是分治左右区间，

找到左区间和右区间的极大值的位置，

然后询问两次，决定是左更大还是右更大

看见neal这个最优次数不超过，补一下

感觉有点哈夫曼树贪心的意思，也有点启发式NTT的合并方式

实际就是当还有x个位置都可以成为答案时，

把他们按位置增序维护在链表里，

每次遍历链表，找到位置最接近的两个数询问

复杂度

构造

根据这个尝试去构造对应的hack方法，

于是，想到的最接近3n方次数的构造方法是

先把n和n-1放两边，n-2放中间，然后递归左右

n=9时，数组形如

9 4 6 3 7 2 5 1 8

证明

 

代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,ll> PI;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define ll long long
#define ull unsigned ll
const int N=2e3+10;
int t,n,dp[N][N];
int cal(int l,int r){if(l==r)return 0;if(~dp[l][r])return dp[l][r];printf("? %d %d\n",l,r);fflush(stdout);int v;scanf("%d",&v);return dp[l][r]=v;
}
void out(int x){printf("! %d\n",x);fflush(stdout);
}
int main(){sci(t);while(t--){sci(n);vector<int>now(n);iota(now.begin(),now.end(),1);rep(i,1,n){rep(j,i,n){dp[i][j]=-1;}}while(SZ(now)>1){int dis=n,p=-1,sz=SZ(now)-1;rep(i,0,sz-1){int w=now[i+1]-now[i];if(w<dis)dis=w,p=i;}int x=cal(now[p],now[p+1]),y=cal(now[p],now[p+1]-1);if(x==y)now.erase(now.begin()+p);else now.erase(now.begin()+(p+1));}out(now[0]);}return 0;
}