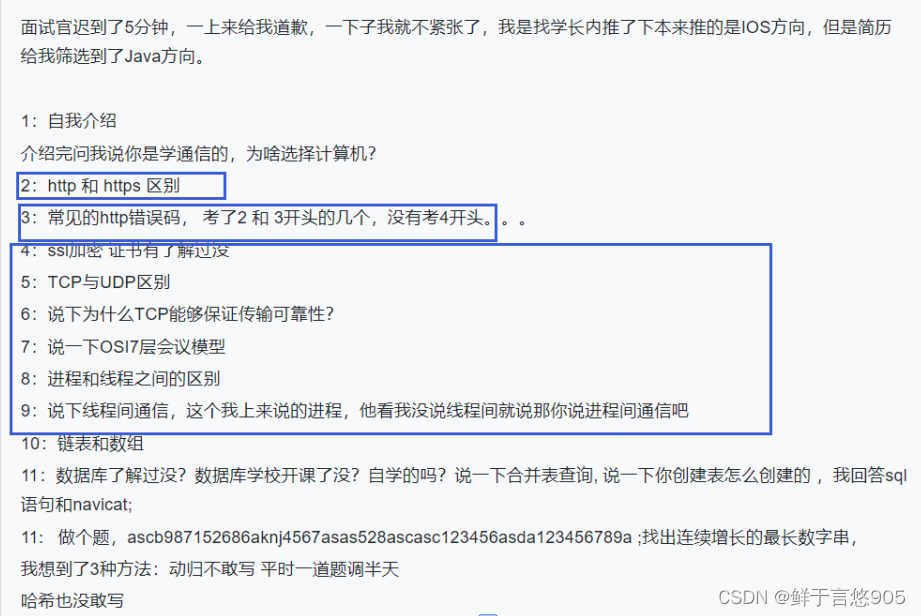
一、ReLU相对于Sigmoid和Tanh的优点
(1)计算效率高
ReLU函数数学形式简单,仅需要对输入进行阈值操作,大于0则保留,小于0则置为0。Sigmoid和Tanh需要指数运算但ReLU不需要。所以相比之下它会更快,降低了神经网络的运行时间和计算资源消耗。
(2)解决梯度消失问题
Sigmoid和Tanh在输入值较大或较小时,其导数接近于0,易导致梯度消失。而ReLU在正区间内导数恒为1,这意味着对于正输入,梯度不会随着网络层的增加而衰减,这有助于解决深度网络中的梯度消失问题。
(3)稀疏激活性
在ReLU中,所有的负输入都会输出0,这导致了网络中的神经元输出是稀疏的,即在任何时候都只有一部分神经元是激活的,这样的稀疏性可以提高网络的表达能力,有助于降低过拟合风险,提高模型的泛化能力。
二、ReLU它的局限性和改进方案
(1)ReLU的局限性
- 神经元死亡问题:这是由于负梯度经过ReLU的时候被置0,且以后也再也不被任何数据激活,即流经该神经元的梯度永远为0,不对任何数据产生响应。如果在实际训练中,如果不恰当的参数初始化或者学习率设置较大,会导致一定比例的神经元会不可逆的死亡,进而参数梯度无法跟新,导致训练失败。
- 非连续梯度问题: ReLU在原点处的梯度突然从1变为0,这种不连续性可能在某些情况下导致训练不稳定。
(2)改进方法
可以采用ReLU的变种Leaky ReLU(LReLU)这个函数的表达式为:
LReLU在正区间的行为与ReLU相同,其中的α是一个很小的正常数。图像如下:
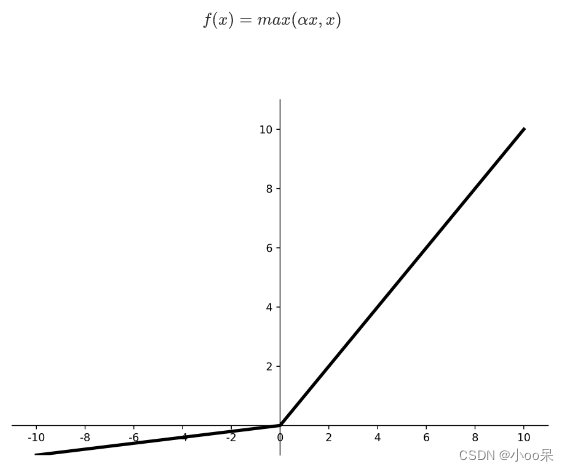
它解决“死神经元”局限性的原理是引入一个小的、固定的梯度α(如α = 0.01), 即使在输入值为负数的情况下也允许神经元有一个小的、非零的梯度。LReLU的这个α值是人为设定的,对所有负值输入统一适用,训练过程中不进行学习或调整。
基于这种思想,参数化的Parametric ReLU (PReLU)应运而生,他和LReLU的主要区别是对于负值输入,PReLU引入了一个可学习的参数α,这里的α不再是一个固定的常数,而是在训练过程中根据反向传播算法和优化过程自动学习得到的,它可以是每个神经元独享的一个参数,也可以是共享于整个网络层的所有神经元。