算法设计与分析实验报告c++实现(TSP问题、哈夫曼编码问题、顾客安排问题、最小生成树问题、图着色问题)

一、实验目的

1．加深学生对贪心算法设计方法的基本思想、基本步骤、基本方法的理解与掌握；
2．提高学生利用课堂所学知识解决实际问题的能力；
3．提高学生综合应用所学知识解决实际问题的能力。

二、实验任务

用贪心算法实现：
1、TSP问题
TSP问题（Travelling Salesman Problem）即旅行商问题，又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
2、哈夫曼编码问题
a.写一个程序，为给定的英文文本构造一套哈夫曼编码，并对该文本编码。
b.写一个程序，对一段用哈夫曼编码的英文文本进行解码。
c.做一个实验，测试对包含1000个词左右的一段英文文本进行哈夫曼编码时，典型的压缩率位于什么样的区间。
3、设有n个顾客同时等待一项服务，顾客i 需要的服务时间为ti ,i=1，2，3，…，n 。从时刻0开始计时，若在时刻t开始对顾客i服务，那么i的等待时间为t,应该怎么安排n个顾客的服务次序使得总的等待时间（每个顾客等待时间的总和）最少？
假设服务时间分别为{1，3，2，15，10，6，12}，用贪心算法给出这个问题的解。
4、最小生成树问题（Prim算法和Kruskal算法）
设G=(V，E)是一个无向连通网，生成树上各边的权值之和称为该生成树的代价，在G的所有生成树中，代价最小的生成树称为最小生成树（Minimal Spanning Trees）。
5、图着色问题
给定无向连通图G=(V, E)，求图G的最小色数k，使得用k种颜色对G中的顶点着色，可使任意两个相邻顶点着色不同。

三、实验设备及编程开发工具

编程开发工具：Microsoft Visual c++

四、实验过程设计（算法设计过程）

（一）TSP问题

1、基本算法思想
贪心算法：又称贪婪算法（greedy algorithm）,该算法是指：在对问题求解时，总是做出当前情况下的最好选择，否则将来可能会后悔，故名“贪心”。这是一种算法策略，每次选择得到的都是局部最优解。选择的策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。
针对TSP问题，使用贪心算法的求解的过程为：
1.从某一个城市开始，每次选择一个城市，直到所有的城市被走完。
2.每次在选择下一个城市的时候，只考虑当前情况，保证迄今为止经过的路径总距离最小。
2、源程序

#include<iostream> 
using namespace std; 
#define n 4 
int main() 
{   int i,j,k,l; int S[n];//用于存储已访问过的城市 int D[n][n];//用于存储两个城市之间的距离 int sum = 0;//用于记算已访问过的城市的最小路径长度 int Dtemp;//保证Dtemp比任意两个城市之间的距离都大（其实在算法描述中更准确的应为无穷大） int flag;最为访问的标志，若被访问过则为1，从未被访问过则为0 /*初始化*/ i = 1;//i是至今已访问过的城市 S[0] = 0; D[0][1] = 2;D[0][2] = 6;D[0][3] = 5;D[1][0] = 2;D[1][2] = 4; D[1][3] = 4;D[2][0] = 6;D[2][1] = 4;D[2][3] = 2;D[3][0] = 5; D[3][1] = 4;D[3][2] = 2; do{ k = 1;Dtemp = 10000; do{ l = 0;flag = 0; do{ if(S[l] == k){//判断该城市是否已被访问过，若被访问过， flag = 1;//则flag为1 break;//跳出循环，不参与距离的比较 }else l++; }while(l < i); if(flag == 0&&D[k][S[i - 1]] < Dtemp){/*D[k][S[i - 1]]表示当前未被访问的城市k与上一个已访问过的城市i-1之间的距离*/ j = k;//j用于存储已访问过的城市k Dtemp = D[k][S[i - 1]];//Dtemp用于暂时存储当前最小路径的值 } k++; }while(k < n);S[i] = j;//将已访问过的城市j存入到S[i]中 i++; sum += Dtemp;//求出各城市之间的最短距离，注意：在结束循环时，该旅行商尚未回到原出发的城市 }while(i < n); sum += D[0][j];//D[0][j]为旅行商所在的最后一个城市与原出发的城市之间的距离 cout<<"经过的城市的路径:";for(j = 0; j < n; j++){ //输出经过的城市的路径 cout<<j<<" "; } cout<<"\n访问过的城市的最小路径长度:"<<sum<<"\n";//求出最短路径的值}

（二）哈夫曼编码问题

1、基本算法思想
哈夫曼提出构造最优前缀码的贪心算法，由此产生的编码方案称为哈夫曼编码。其构造步骤如下：
(1)哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。
(2)算法以|C|个叶结点开始，执行|C|－1次的“合并”运算后产生最终所要求的树T。
(3)假设编码字符集中每一字符c的频率是f©。
以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。
一旦2棵具有最小频率的树合并后，产生一棵新的树，其频率为合并的2棵树的频率之和，并将新树插入优先队列Q。
经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树T。.
2、源程序

#include<iostream>  
#include<string>  
using namespace std;
struct Node
{double weight;  string ch;  string code; int lchild, rchild, parent;
};void Select(Node huffTree[], int *a, int *b, int n)//找权值最小的两个a和b  
{int i;double weight = 0; //找最小的数for (i = 0; i <n; i++){if (huffTree[i].parent != -1)     //判断节点是否已经选过continue;else{if (weight == 0){weight = huffTree[i].weight;*a = i;}else{if (huffTree[i].weight < weight){weight = huffTree[i].weight;*a = i;}}}}weight = 0; //找第二小的数for (i = 0; i < n; i++){if (huffTree[i].parent != -1 || (i == *a))//排除已选过的数continue;else{if (weight == 0){weight = huffTree[i].weight;*b = i;}else{if (huffTree[i].weight  < weight){weight = huffTree[i].weight;*b = i;}}}}int temp;if (huffTree[*a].lchild < huffTree[*b].lchild)  //小的数放左边{temp = *a;*a = *b;*b = temp;}
}void Huff_Tree(Node huffTree[], int w[], string ch[], int n)
{for (int i = 0; i < 2 * n - 1; i++) //初始过程{huffTree[i].parent = -1;    huffTree[i].lchild = -1;    huffTree[i].rchild = -1;  huffTree[i].code = "";}for (int i = 0; i < n; i++)       {huffTree[i].weight = w[i];  huffTree[i].ch = ch[i];     }for (int k = n; k < 2 * n - 1; k++){int i1 = 0;int i2 = 0;Select(huffTree, &i1, &i2, k); //将i1，i2节点合成节点khuffTree[i1].parent = k;   huffTree[i2].parent = k;huffTree[k].weight = huffTree[i1].weight + huffTree[i2].weight;huffTree[k].lchild = i1;huffTree[k].rchild = i2;}
}void Huff_Code(Node huffTree[], int n)
{int i, j, k;string s = "";for (i = 0; i < n; i++)  {s = "";         j = i;                while (huffTree[j].parent != -1) //从叶子往上找到根节点{k = huffTree[j].parent;if (j == huffTree[k].lchild) //如果是根的左孩子，则记为0{s = s + "0";}else               {s = s + "1";}j = huffTree[j].parent; }cout << "字符 " << huffTree[i].ch << " 的编码：";for (int l = s.size() - 1; l >= 0; l--)    {cout << s[l];huffTree[i].code += s[l]; //保存编码}cout << endl;}
}
string Huff_Decode(Node huffTree[], int n,string s)
{cout << "解码后为：";string temp = "",str="";//保存解码后的字符串for (int i = 0; i < s.size(); i++){temp = temp + s[i];for (int j = 0; j < n; j++){    if (temp == huffTree[j].code){str=str+ huffTree[j].ch;temp = "";break;}    else if (i == s.size()-1&&j==n-1&&temp!="")//全部遍历后没有{str= "解码错误！";}}}return str;
}int main()
{//编码过程const int n=5;Node huffTree[2 * n];string str[] = { "A", "B", "C", "D", "E"};int w[] = { 30, 30, 5, 20, 15 };Huff_Tree(huffTree, w, str, n);Huff_Code(huffTree, n);//解码过程string s;cout << "输入编码：";cin >> s;cout << Huff_Decode(huffTree, n, s)<< endl;;system("pause");return 0;
}

（三）动态服务问题

1、基本算法思想
如果f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是：f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}
这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下：“将前i件物品放入容量为v的背包中”这个子问题，若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”，价值为f[i-1][v]；如果放第i件物品，那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”，此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。
2、源程序

#include <iostream>
#include<cstdio>
#define N 100
#define MAX(a,b) a < b ? b : a
using namespace std;struct goods{
int sign;//物品序号
int wight;//物品重量
int value;//物品价值
};int n,bestValue,cv,cw,C;//物品数量，价值最大，当前价值，当前重量，背包容量
int X[N],cx[N];//最终存储状态，当前存储状态
struct goods goods[N];int KnapSack(int n,struct goods a[],int C,int x[]){int V[N][10*N];for(int i = 0; i <= n; i++)//初始化第0列V[i][0] = 0;for(int j = 0; j <= C; j++)//初始化第0行V[0][j] = 0;for(int i = 1; i <= n; i++)for(int j = 1; j <= C; j++)if(j < a[i-1].wight)V[i][j] = V[i-1][j];elseV[i][j] = MAX(V[i-1][j],V[i-1][j-a[i-1].wight] + a[i-1].value);for(int i = n,j = C; i > 0; i--){if(V[i][j] > V[i-1][j]){x[i-1] = 1;j = j - a[i-1].wight;}elsex[i-1] = 0;}return V[n][C];
}
int main()
{printf("物品种类n：");scanf("%d",&n);printf("背包容量C：");scanf("%d",&C);for(int i = 0; i < n; i++){printf("物品%d的重量w[%d]及其价值v[%d]：",i+1,i+1,i+1);scanf("%d%d",&goods[i].wight,&goods[i].value);}int sum2 = KnapSack(n,goods,C,X);printf("动态规划法求解0/1背包问题:\nX=[");for(int i = 0; i < n; i++)cout<<X[i]<<" ";//输出所求X[n]矩阵printf("]   装入总价值%d\n", sum2);return 0;
}

（四）最小生成树问题

1、基本算法思想
Prim算法
1.概览
普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点（英语：Vertex (graph theory)），且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

2.算法简单描述
1).输入：一个加权连通图，其中顶点集合为V，边集合为E；
2).初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；
3).重复下列操作，直到Vnew = V：
a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；
4).输出：使用集合Vnew和Enew来描述所得到的最小生成树。

Kruskal算法是一种用来寻找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

2.算法简单描述
1).记Graph中有v个顶点，e个边
2).新建图Graphnew，Graphnew中拥有原图中相同的e个顶点，但没有边
3).将原图Graph中所有e个边按权值从小到大排序
4).循环：从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中 if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中添加这条边到图Graphnew中
2、源程序

Prim算法

#include <iostream>
#include <vector>
using namespace std;//Prim算法实现
void prim_test()
{int n;cin >> n;vector<vector<int> > A(n, vector<int>(n));for(int i = 0; i < n ; ++i) {for(int j = 0; j < n; ++j) {cin >> A[i][j];}}int pos, minimum;int min_tree = 0;//lowcost数组记录每2个点间最小权值，visited数组标记某点是否已访问vector<int> visited, lowcost;for (int i = 0; i < n; ++i) {visited.push_back(0);    //初始化为0，表示都没加入}visited[0] = 1;   //最小生成树从第一个顶点开始for (int i = 0; i < n; ++i) {lowcost.push_back(A[0][i]);    //权值初始化为0}for (int i = 0; i < n; ++i) {    //枚举n个顶点minimum = max_int;for (int j = 0; j < n; ++j) {    //找到最小权边对应顶点if(!visited[j] && minimum > lowcost[j]) {minimum = lowcost[j];pos = j;}}if (minimum == max_int)    //如果min = max_int表示已经不再有点可以加入最小生成树中break;min_tree += minimum;visited[pos] = 1;     //加入最小生成树中for (int j = 0; j < n; ++j) {if(!visited[j] && lowcost[j] > A[pos][j]) lowcost[j] = A[pos][j];   //更新可更新边的权值}}cout << min_tree << endl;
}int main(void)
{prim_test();return 0;
}

Kruskal算法

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;//并查集实现最小生成树
vector<int> u, v, weights, w_r, father;
int mycmp(int i, int j)
{return weights[i] < weights[j];
}
int find(int x)
{return father[x] == x ? x : father[x] = find(father[x]);
}
void kruskal_test()
{int n;cin >> n;vector<vector<int> > A(n, vector<int>(n));for(int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {cin >> A[i][j];}}int edges = 0;// 共计n*(n - 1)/2条边for (int i = 0; i < n - 1; ++i) {for (int j = i + 1; j < n; ++j) {u.push_back(i);v.push_back(j);weights.push_back(A[i][j]);w_r.push_back(edges++);}}for (int i = 0; i < n; ++i) {father.push_back(i);    // 记录n个节点的根节点，初始化为各自本身}sort(w_r.begin(), w_r.end(), mycmp); //以weight的大小来对索引值进行排序int min_tree = 0, cnt = 0;for (int i = 0; i < edges; ++i) {int e = w_r[i];    //e代表排序后的权值的索引int x = find(u[e]), y = find(v[e]);//x不等于y表示u[e]和v[e]两个节点没有公共根节点，可以合并if (x != y) {min_tree += weights[e];father[x] = y;++cnt;}}if (cnt < n - 1) min_tree = 0;cout << min_tree << endl;
}int main(void)
{kruskal_test();return 0;
}

（五）图着色问题

1、基本算法思想
图的m色优化问题:给定无向连通图G,为图G的各顶点着色, 使图中任2邻接点着不同颜色,问最少需要几种颜色。所需的最少颜色的数目m称为该图的色数。
若图G是可平面图,则它的色数不超过4色(4色定理).
4色定理的应用:在一个平面或球面上的任何地图能够只用4种
颜色来着色使得相邻的国家在地图上着有不同颜色
2、源程序

#include<stdio.h>int color[100];
//int c[100][100];
bool ok(int k ,int c[][100])//判断顶点k的着色是否发生冲突
{int i,j;for(i=1;i<k;i++)if(c[k][i]==1&&color[i]==color[k])return false;return true;
}void graphcolor(int n,int m,int c[][100])
{int i,k;for(i=1;i<=n;i++)color[i]=0;//初始化k=1;while(k>=1){color[k]=color[k]+1;while(color[k]<=m)if (ok(k,c)) break;else color[k]=color[k]+1;//搜索下一个颜色if(color[k]<=m&&k==n)//求解完毕，输出解{for(i=1;i<=n;i++)printf("%d ",color[i]);printf("\n");//return;//return表示之求解其中一种解}else if(color[k]<=m&&k<n)k=k+1;    //处理下一个顶点else{color[k]=0;k=k-1;//回溯}}
}
void main()
{int i,j,n,m;int c[100][100];//存储n个顶点的无向图的数组printf("输入顶点数n和着色数m:\n");scanf("%d %d",&n,&m);printf("输入无向图的邻接矩阵:\n");for(i=1;i<=n;i++)for(j=1;j<=n;j++)scanf("%d",&c[i][j]);printf("着色所有可能的解:\n");graphcolor(n,m,c);
}

五、实验结果及算法复杂度分析
（一）TSP问题
1、实验结果

img

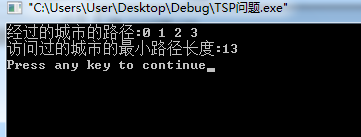
2、时间复杂度
时间复杂度为O(n)
（二）哈夫曼编码问题
1、实验结果

img

2、时间复杂度
时间复杂度为 O ( n m 2 ) O(nm^2) O(nm2)
（三）动态服务问题

img

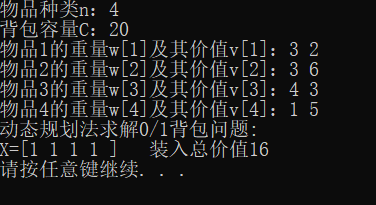
2、时间复杂度
时间复杂度为O(n)
（四）最小生成树问题
时间复杂度
Prim算法时间复杂度为邻接矩阵: O ( v 2 ) O(v^2) O(v2)邻接表: O ( e l o g 2 v ) O(elog2v) O(elog2v)

Kruskal算法时间复杂度为 O ( e l o g 2 e ) O(elog2e) O(elog2e)

（五）图着色问题
1、实验结果

img

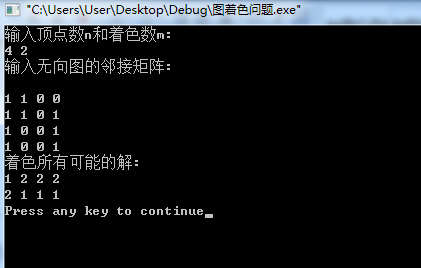
2、时间复杂度
时间复杂度为 O ( n 2 ) O(n^2) O(n2)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/617197.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

C# Solidworks二次开发：相机访问相关API详解

C# Solidworks二次开发：相机访问相关API详解

大家好&#xff0c;今天要介绍的API为相机相关的API&#xff0c;这篇文章比较适合女孩子&#xff0c;学会了相机就会拍照了&#xff0c;哈哈。 下面是要介绍的API: &#xff08;1&#xff09;第一个为GetFocalDistance&#xff0c;这个API的含义为获取相机的焦距&#xff0c;…
阅读更多...
共享内存及共享内存实现进程间通信

共享内存及共享内存实现进程间通信

个人主页&#xff1a;Lei宝啊 愿所有美好如期而遇 我们知道&#xff0c;进程是具有独立性的&#xff0c;什么叫进程具有独立性&#xff1f;就是说&#xff0c;每一个进程都有他们自己的虚拟地址空间&#xff0c;而虚拟进程空间里的虚拟地址通过页表映射到不同的物理内存上&am…
阅读更多...
电池电量监测系统设计 单片机+LabVIEW+Matlab+Protues+Keil程序

电池电量监测系统设计 单片机+LabVIEW+Matlab+Protues+Keil程序

目录 前言 提供 软件 系统展示 1.放电试验及其处理 2.硬件系统原理图 3.下位机程序 4.显示 5.上位机界面 6.上位机程序 7.文档 资料下载地址&#xff1a;电池电量监测系统设计 单片机LabVIEWMatlabProtuesKeil程序 前言 这套系统首先使用Matlab分析获得了电压…
阅读更多...
【Java系列】SpringCloudAlibaba统一返回体及全局异常捕获实现

【Java系列】SpringCloudAlibaba统一返回体及全局异常捕获实现

本文将以实际代码展示如何实现SpringCloudAlibaba的统一返回体及全局异常捕获。 作者&#xff1a;后端小肥肠 1. 前言 在构建微服务应用时&#xff0c;统一返回体和异常捕获机制的设计对于保持代码的整洁性和提高服务的可维护性至关重要。特别是在使用 Spring Boot 和 Spring …
阅读更多...
DataX案例，MongoDB数据导入HDFS与MySQL

DataX案例，MongoDB数据导入HDFS与MySQL

【尚硅谷】Alibaba开源数据同步工具DataX技术教程_哔哩哔哩_bilibili 目录 1、MongoDB 1.1、MongoDB介绍 1.2、MongoDB基本概念解析 1.3、MongoDB中的数据存储结构 1.4、MongoDB启动服务 1.5、MongoDB小案例 2、DataX导入导出案例 2.1、读取MongoDB的数据导入到HDFS 2…
阅读更多...
Re65：读论文 GPT-3 Language Models are Few-Shot Learners

Re65：读论文 GPT-3 Language Models are Few-Shot Learners

诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文全名&#xff1a;Language Models are Few-Shot Learners ArXiv网址&#xff1a;https://arxiv.org/abs/2005.14165 2020 NeurIPS&#xff1a;https://papers.nips.cc/paper/2020/hash/1457c0d6bfcb49674…
阅读更多...
UVa1313/LA2693 Ghost Busters

UVa1313/LA2693 Ghost Busters

UVa1313/LA2693 Ghost Busters 题目链接题意分析AC代码 题目链接 本题是2002年ICPC欧洲区域赛东北欧赛区的G题 题意 有 N ( N ≤ 100 ) N(N≤100) N(N≤100)个鬼&#xff0c;每个鬼是中心在 ( X i , Y i , Z i ) ( 1 ≤ X i , Y i , Z i ≤ 10000 ) (X_i,Y_i,Z_i) (1 ≤ X_i,Y…
阅读更多...
Python中的回调函数和C中函数指针什么关系？

Python中的回调函数和C中函数指针什么关系？

你好&#xff0c;我是安然无虞。 Python 回调 在Python中&#xff0c;‘回调函数’ (callback) 是指一个作为参数传递给其它代码的函数。 目的是在后者完成某些操作后调用这个传递进来的函数。 回调允许在执行异步操作或处理事件时通知调用者代码。 回调函数通常用于&#…
阅读更多...
【数据结构】-- 单链表 vs 双向链表

【数据结构】-- 单链表 vs 双向链表

&#x1f308; 个人主页&#xff1a;白子寰 &#x1f525; 分类专栏&#xff1a;python从入门到精通&#xff0c;魔法指针&#xff0c;进阶C&#xff0c;C语言&#xff0c;C语言题集&#xff0c;C语言实现游戏&#x1f448; 希望得到您的订阅和支持~ &#x1f4a1; 坚持创作博文…
阅读更多...
react query 学习笔记

react query 学习笔记

文章目录 react query 学习笔记查询客户端 QueryClient获取查询客户端 useQueryClient异步重新请求数据 queryClient.fetchQuery /使查询失效 queryClient.invalidateQueries 与 重新请求数据queryClient.refetchQueries 查询 QueriesuseQuery查询配置对象查询的键值 Query Key…
阅读更多...
力扣 | 24. 两两交换链表中的节点

力扣 | 24. 两两交换链表中的节点

两两交换链表中的节点 给定一个链表&#xff0c;两两交换其中相邻的节点&#xff0c;并返回交换后的链表。 你不能只是单纯的改变节点内部的值&#xff0c;而是需要实际的进行节点交换。 输入&#xff1a;head 1->2->3->4->5->NULL 输出&#xff1a;2->1-&g…
阅读更多...
互联网轻量级框架整合之MyBatis核心组件

互联网轻量级框架整合之MyBatis核心组件

在看本篇内容之前&#xff0c;最好先理解一下Hibernate和MyBatis的本质区别&#xff0c;这篇Hibernate和MyBatis使用对比实例做了实际的代码级对比&#xff0c;而MyBatis作为更适合互联网产品的持久层首选必定有必然的原因 MyBatis核心组件 MyBatis能够成为数据持久层首选框&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023