Day 15 重温宝可梦分类器 – 浅谈机器学习基本原理
REview 见我之前的笔记即可~

More parameters , easier to overfit ,why ?

Step 1 a function (Based on domain knowedge)

线条的复杂程度?
Edge Detction

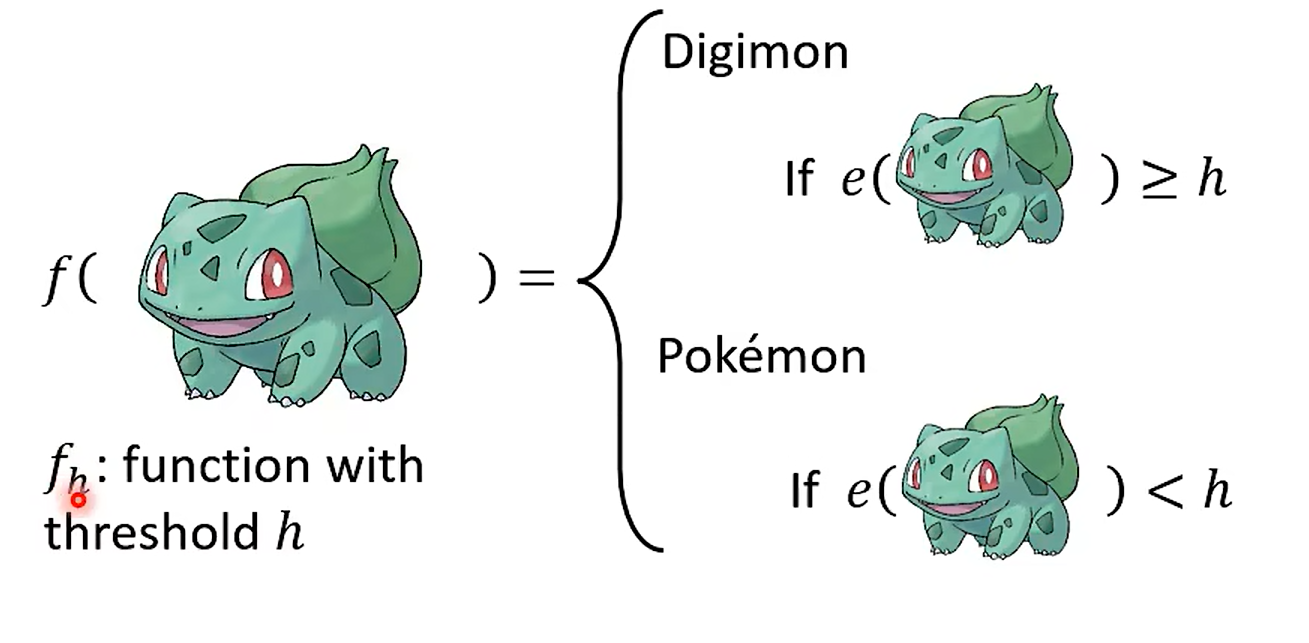
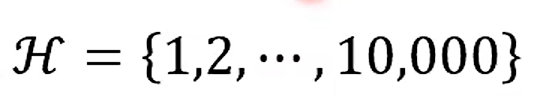

Step 2 Loss
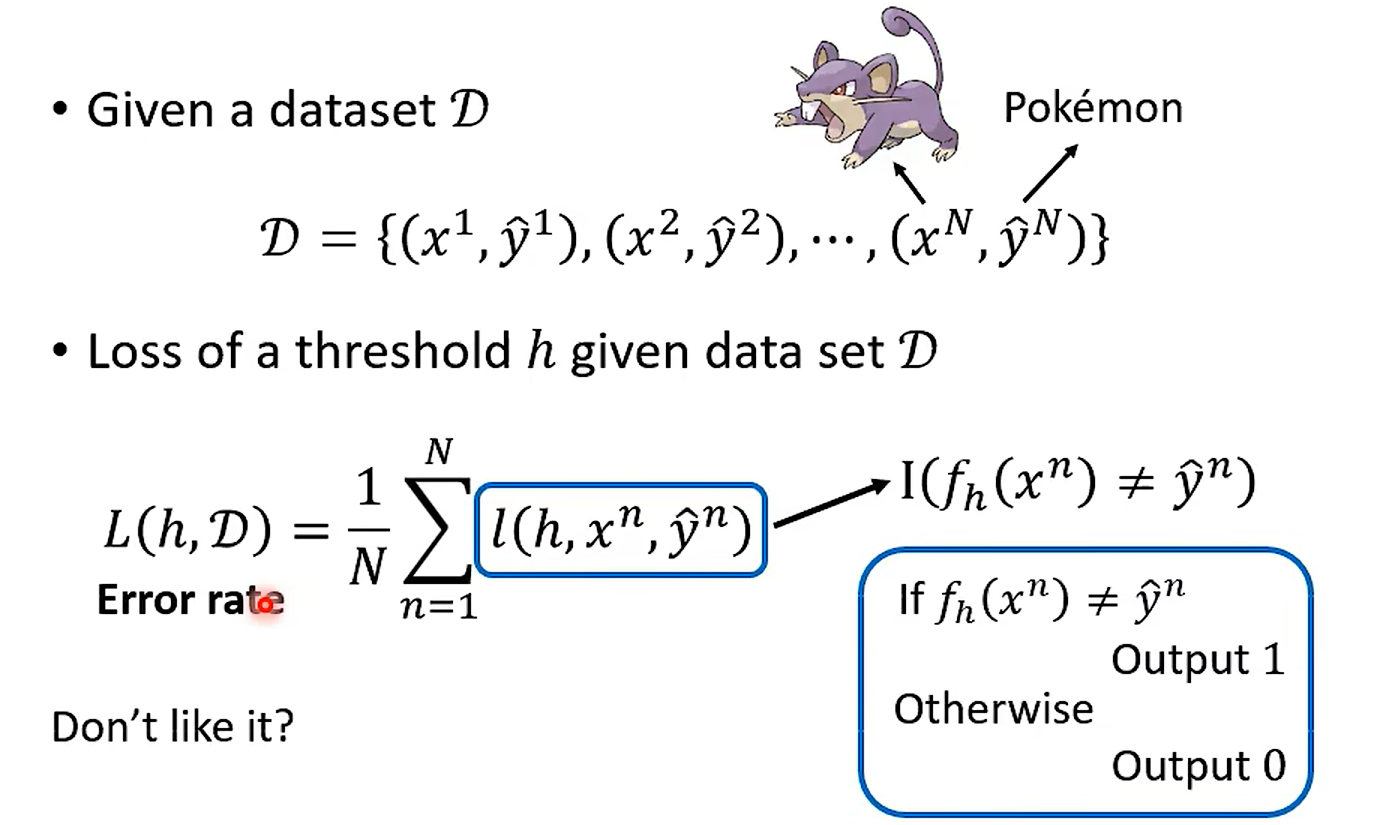

这里注意一下哈,这个corss-entropy 不能直接微分, 那就直接爆搜
step 3 Train find the best


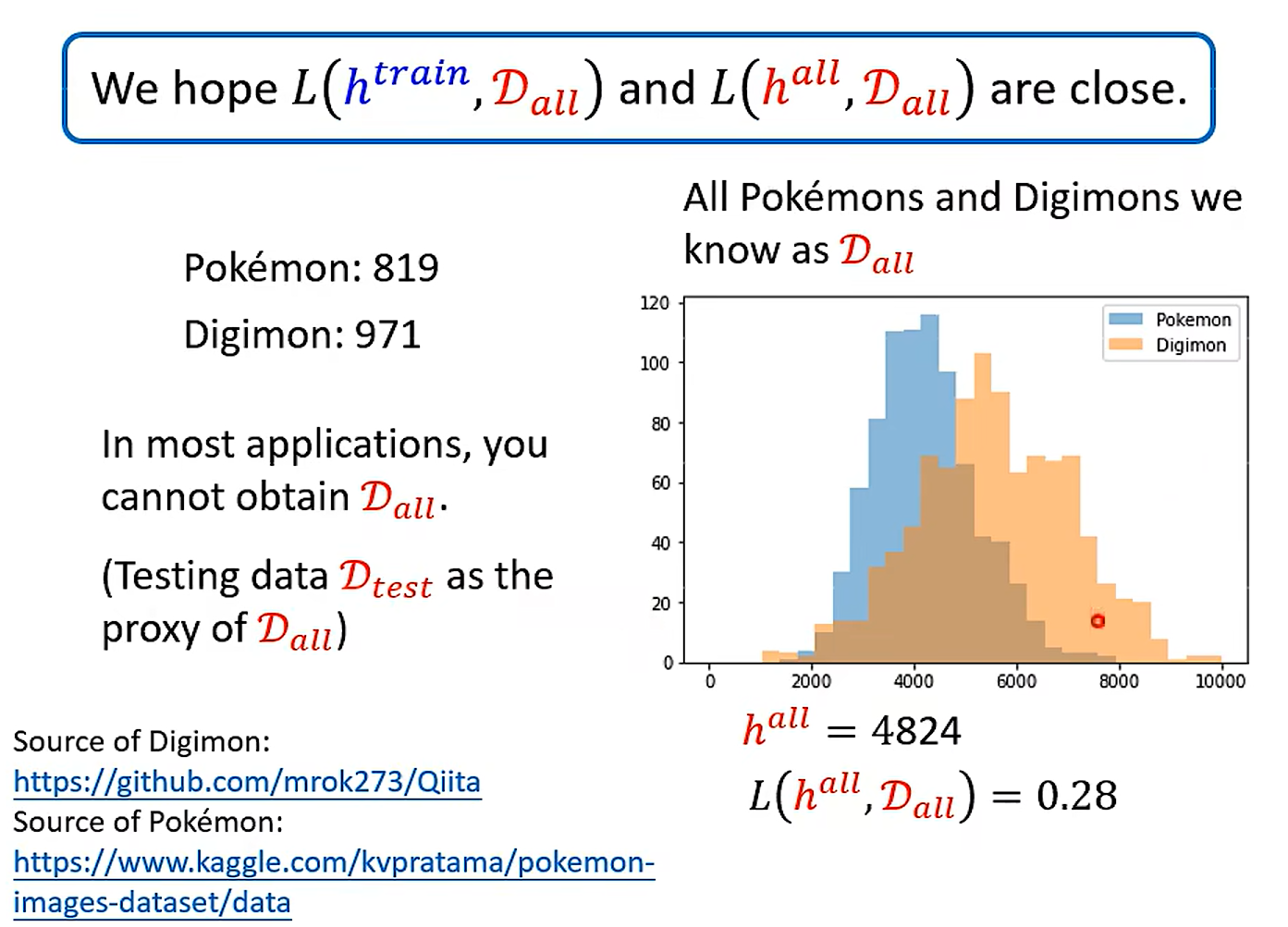
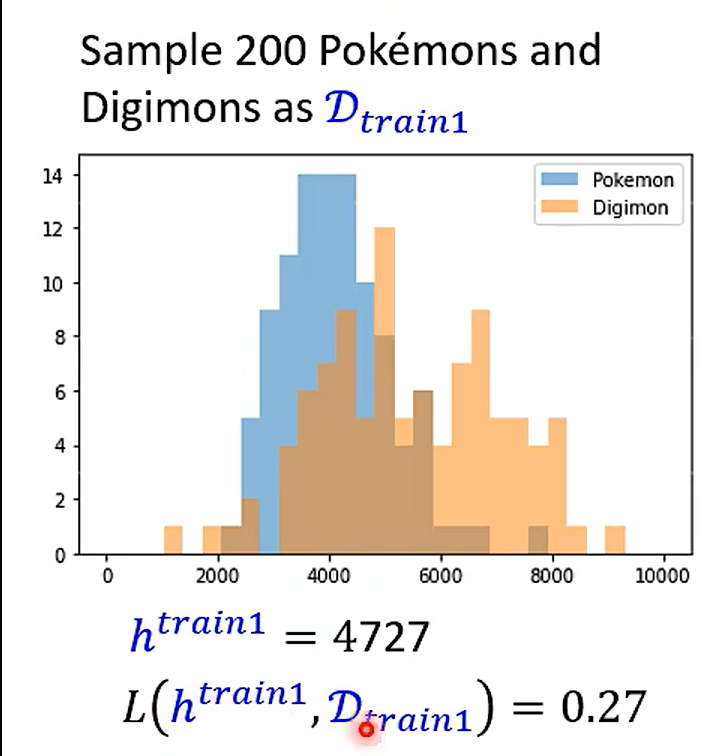

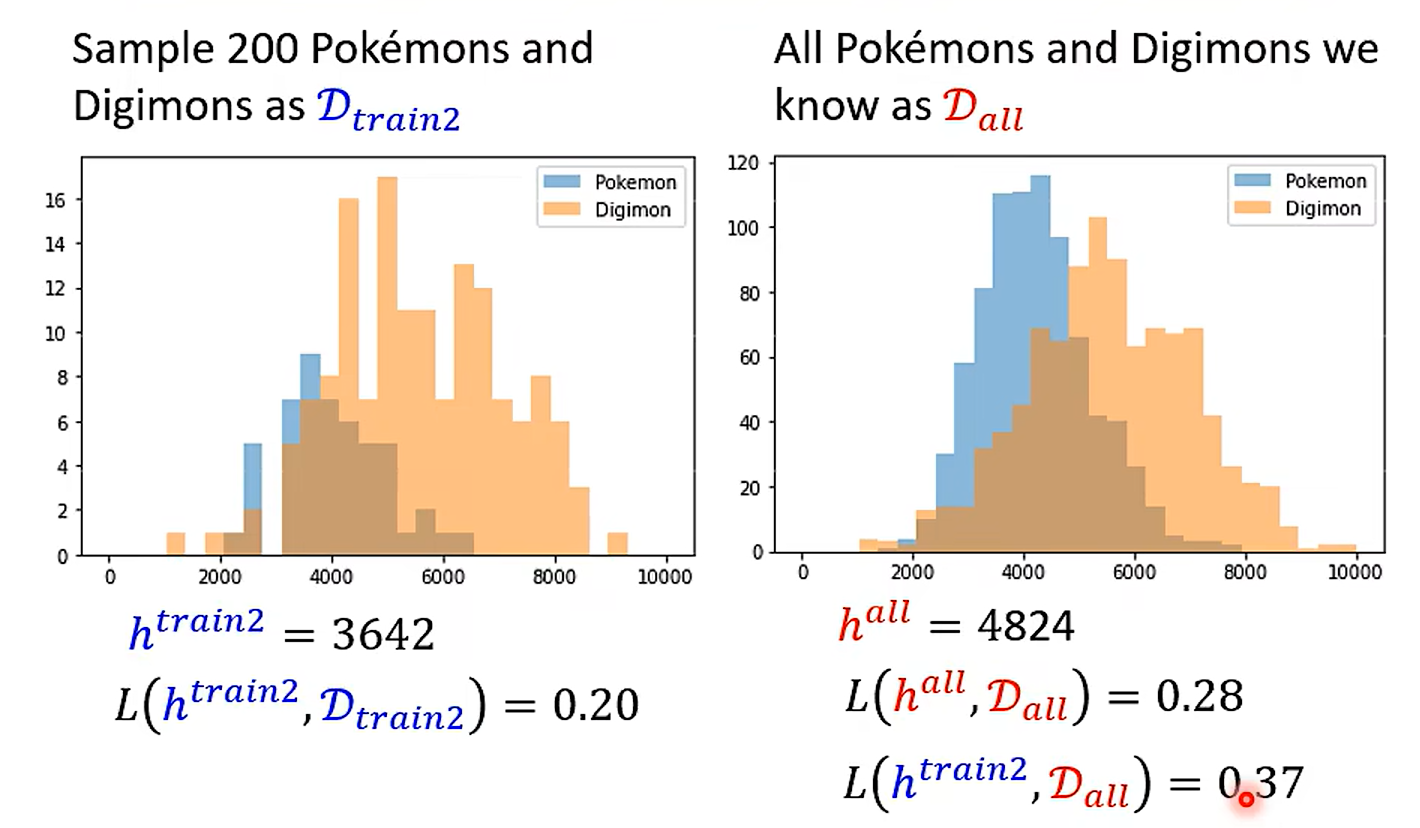


What is the probability of sampling bad Dtrain ?
万能近似!

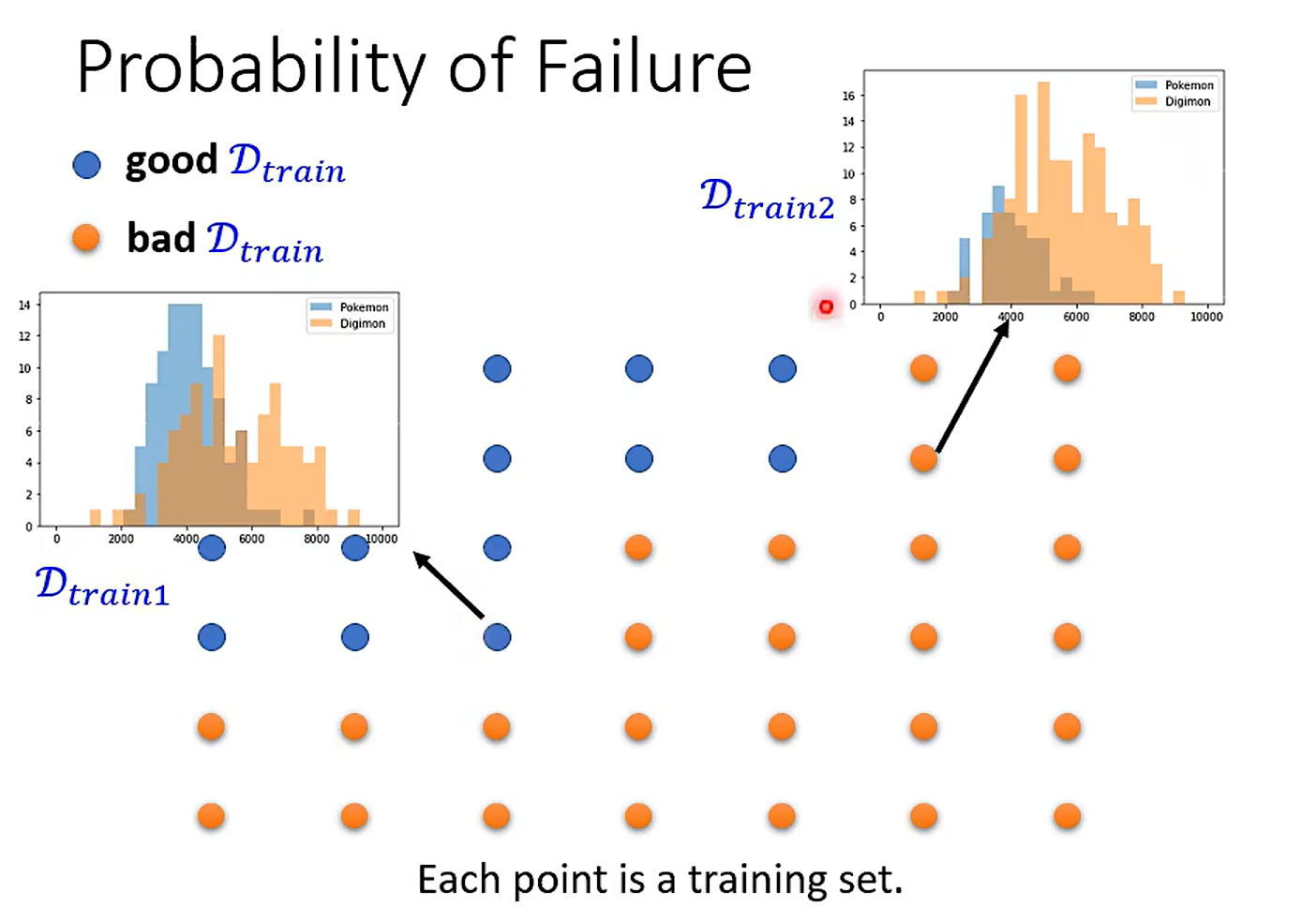

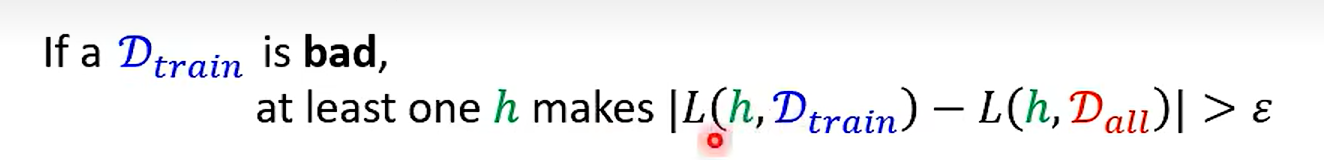
不等式变号即可
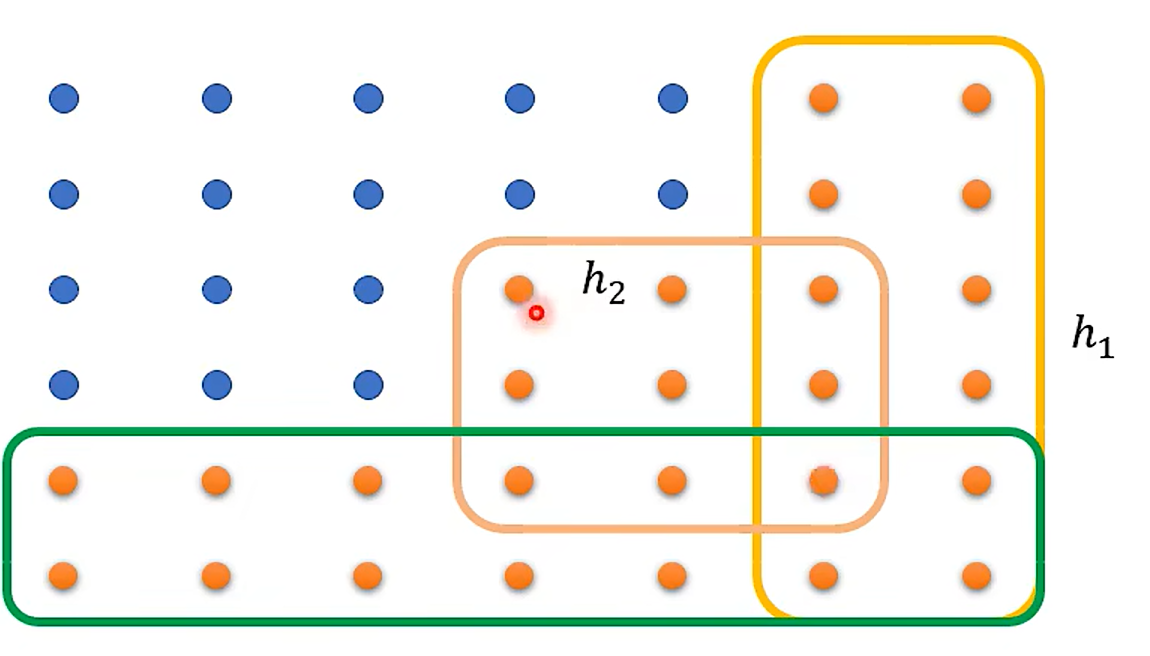

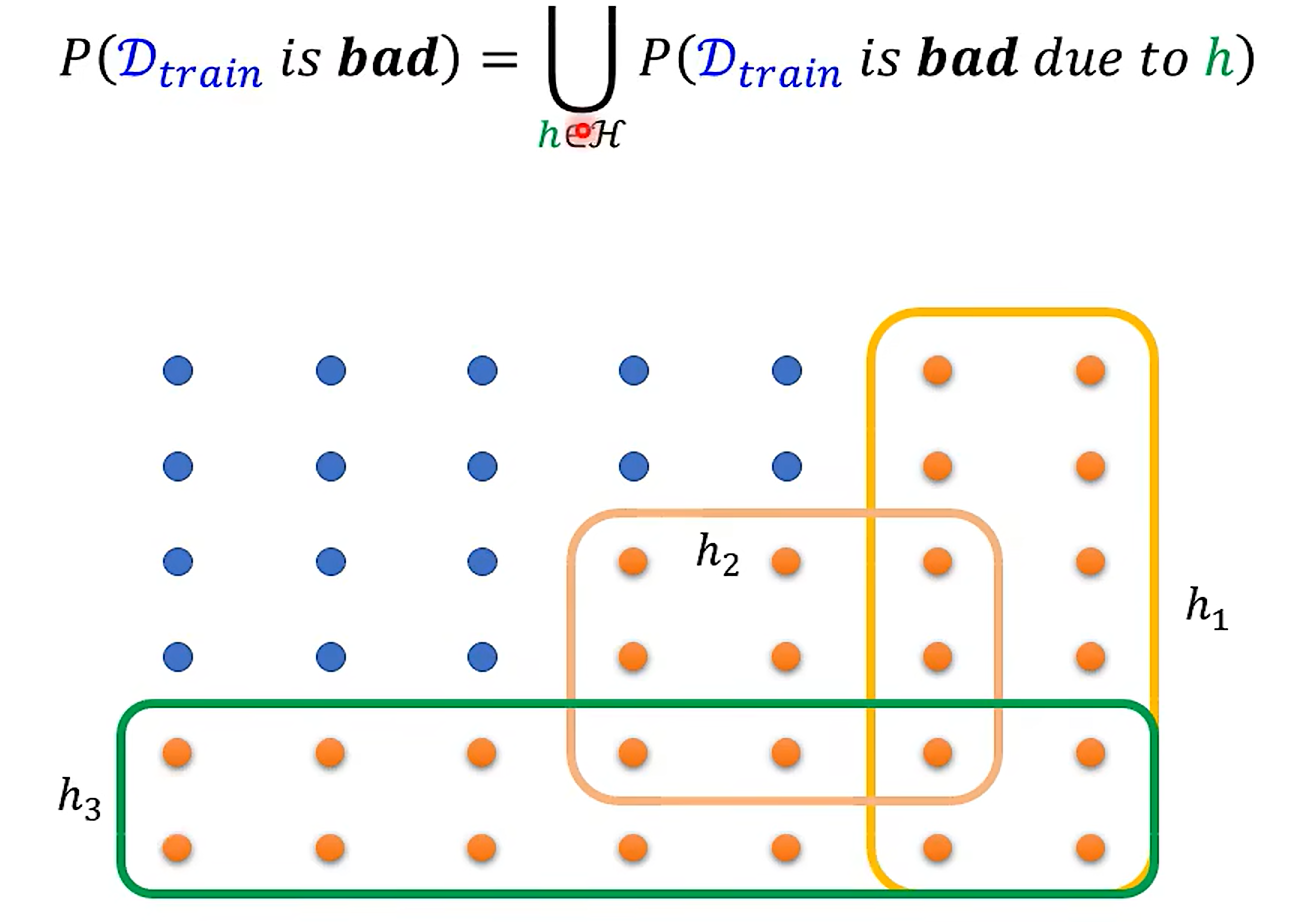

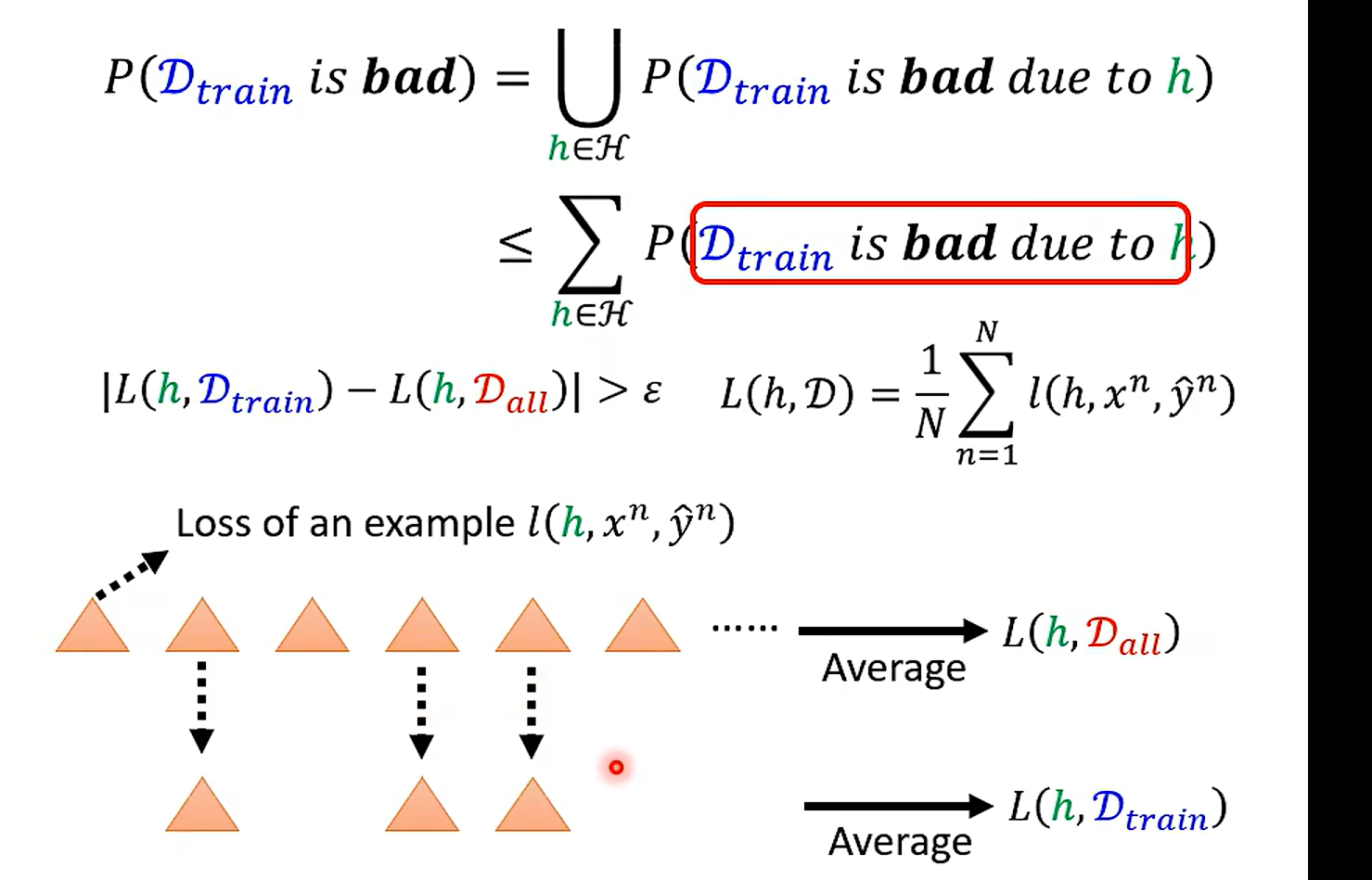
这里应该用数理统计那块儿东西可以做
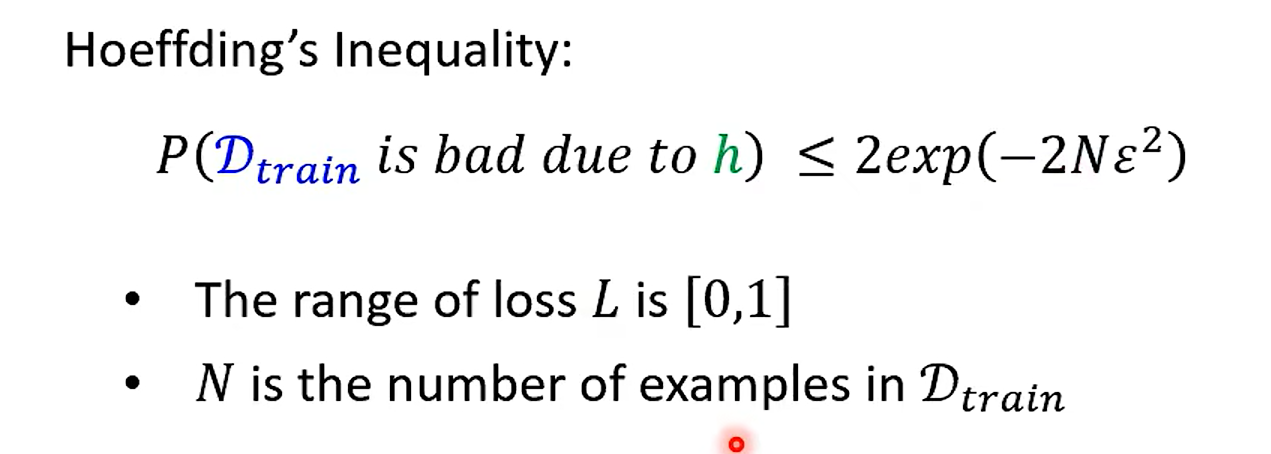
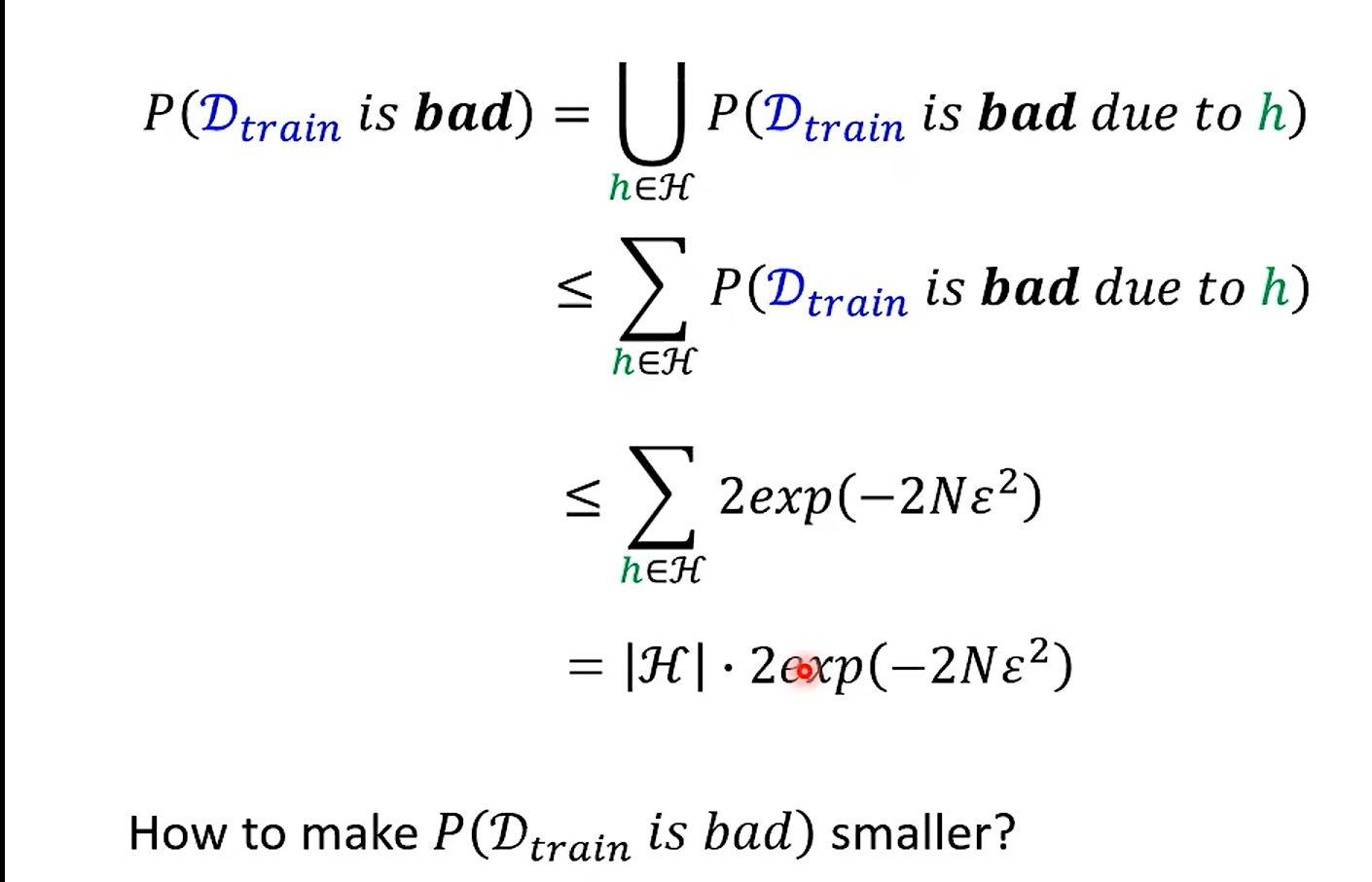

霍夫丁不等式(Hoeffding’s Inequality)是概率论中的一个重要结果,它提供了一种评估独立随机变量之和与其期望值偏差的概率的方法。具体地,如果有一组独立的随机变量,每个随机变量的取值范围都是有限的,那么这些随机变量之和的实际观察值与其期望值的偏差超过某个界限的概率是非常小的。
霍夫丁不等式的数学表达式是这样的:
这两个不等式给出了随机变量之和大于或小于其期望值一定范围的概率上限。
根据霍夫丁不等式,如果在足够大的训练集上,算法的误差已经非常小,那么我们有很强的信心认为,在未知的测试集上,算法的误差也会控制在一个很小的范围内
tmd 不推了暂时,推的我脑袋疼,缓一缓哈 缓一缓

具体参考
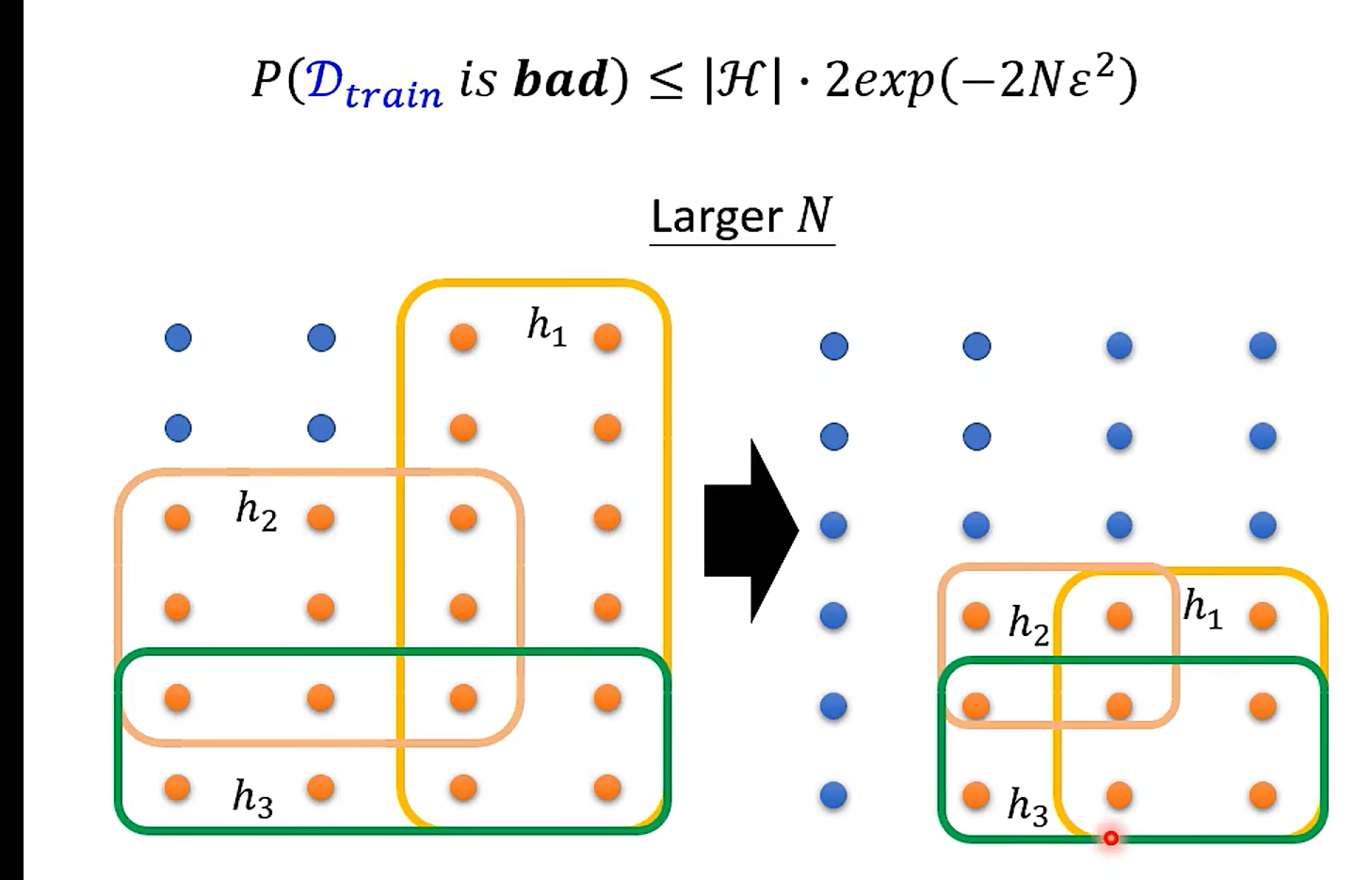
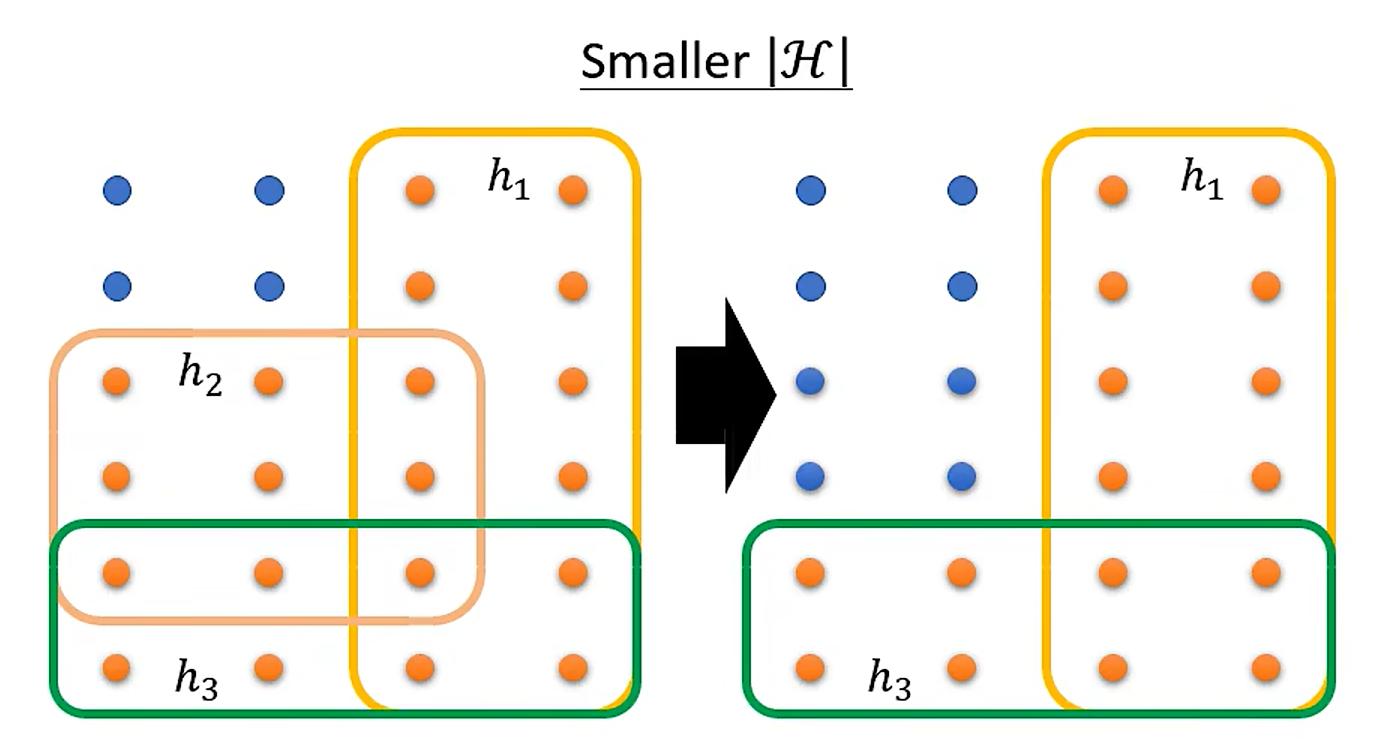
Example



这个问题真的提的很好啊! 如果是连续的怎么办呢? 连续的时候 用VC-dimention 来算模型的 复杂程度

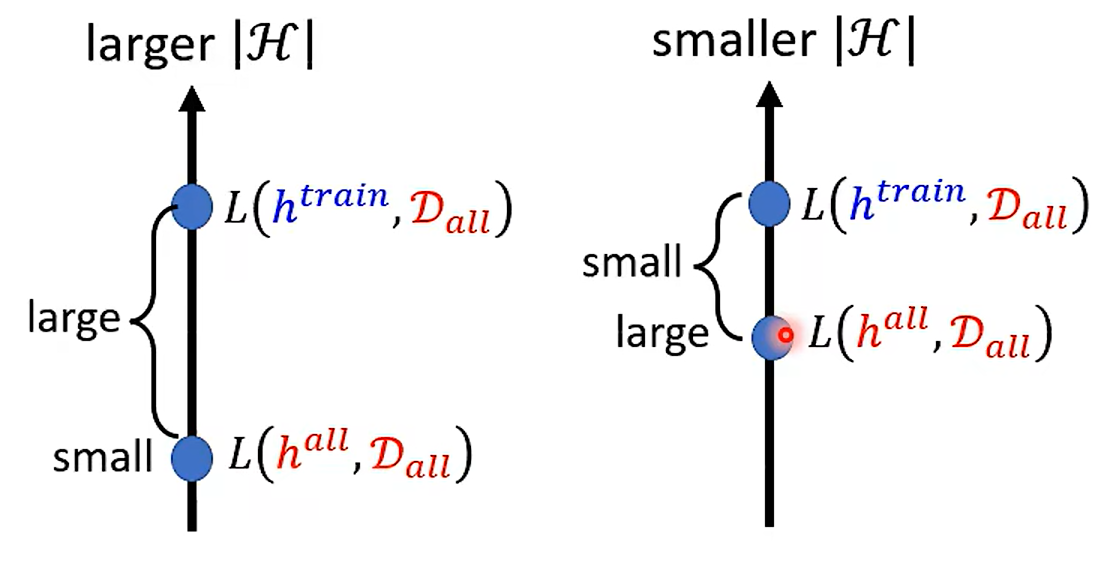
怎么办?
见下一节鱼与熊掌兼得 – Deep Learning