每日OJ题_01背包④_力扣1049. 最后一块石头的重量 II-编程知识

每日OJ题_01背包④_力扣1049. 最后一块石头的重量 II

力扣1049. 最后一块石头的重量 II

问题解析

解析代码

滚动数组优化代码

力扣1049. 最后一块石头的重量 II

1049. 最后一块石头的重量 II

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]
输出：5

提示：

1 <= stones.length <= 30
1 <= stones[i] <= 100

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {}
};

问题解析

先看能不能转化成常见的背包模型问题。

任意两块石头在⼀起粉碎，重量相同的部分会被丢掉，重量有差异的部分会被留下来。那就相当于在原始的数据的前面，加上加号或者减号，是最终的结果最小即可。也就是说把原始的石头分成两部分，两部分的和越接近越好。
又因为当所有元素的和固定时，分成的两部分越接近数组总和的一半，两者的差越小。

因此问题就变成了：在数组中选择一些数，让这些数的和尽量接近 sum / 2 ，如果把数看成物品，每个数的值看成体积和价值，问题就变成了01 背包问题。

以某个位置为结尾，结合题目要求，定义一个状态表示：

dp[i][j] 表示：在前 i 个元素中选择，总和不超过 j，此时所有元素的最大和。

状态转移方程：

dp 状态转移方程分析方式，一般都是根据最后一步的状况，来分情况讨论：

不选 stones[i] ：那么是否能够凑成总和为 j ，就要看在前 i - 1 个元素中选，能否凑成总和为 j 。根据状态表示，此时 dp[i][j] = dp[i - 1][j] ; 。
选择 stones[i] ：这种情况下是有前提条件的，此时的 j 应该大于等于 stones[i] 。因为如果这个元素都比要凑成的总和大，选择它就没有意义。那么是否能够凑成总和为 j ，就要看在前 i - 1 个元素中选，能否凑成总和为 j - stones[i] 。根据状态表示，此时 dp[i][j] = dp[i - 1][j - stones[i]] + stones[i] （ j >= stones[i] ）。

综上所述，我们要的是最大价值。因此，状态转移方程为： if(j >= stones[i]) dp[i][j] = max(dp[i - 1][j] , dp[i - 1][j - stones[i]] + stones[i]) ; else dp[i][j] = dp[i - 1][j] ;（如果多加一行一列，找原数组下标要减1）

初始化：多加一行一列，方便初始化，由于需要用到上一行的数据，因此可以先把第一行初始化。第一行表示没有石子。因此想凑成目标和 j ，最大和都是 0 。

填表顺序：根据状态转移方程，需要从上往下填写每一行，每一个的顺序是任意的。

返回值：根据状态表示，先找到最接近 sum / 2 的最大和 dp[n][sum / 2] ；因为我们要的是两堆石子的差，因此返回 sum - 2 * dp[n][sum / 2] 。

解析代码

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0, n = stones.size();for(auto& e : stones){sum += e;}vector<vector<int>> dp(n + 1, vector<int>(sum / 2 + 1, 0));for(int i = 1; i <= n; ++i){for(int j = 0; j <= sum / 2; ++j){if(j >= stones[i - 1])dp[i][j] = max(dp[i - 1][j] , dp[i - 1][j - stones[i - 1]] + stones[i - 1]) ;elsedp[i][j] = dp[i - 1][j];}}return sum - 2 * dp[n][sum / 2];}
};

滚动数组优化代码

背包问题基本上都是利用滚动数组来做空间上的优化：（时间也有常数的优化）

利用滚动数组优化。
直接在原始代码上修改。

在01背包问题中，优化的结果为：

删掉所有的横坐标。
修改一下 j 的遍历顺序。

（滚动数组优化代码只需能在原代码上修改就行，不用考虑什么状态表示）

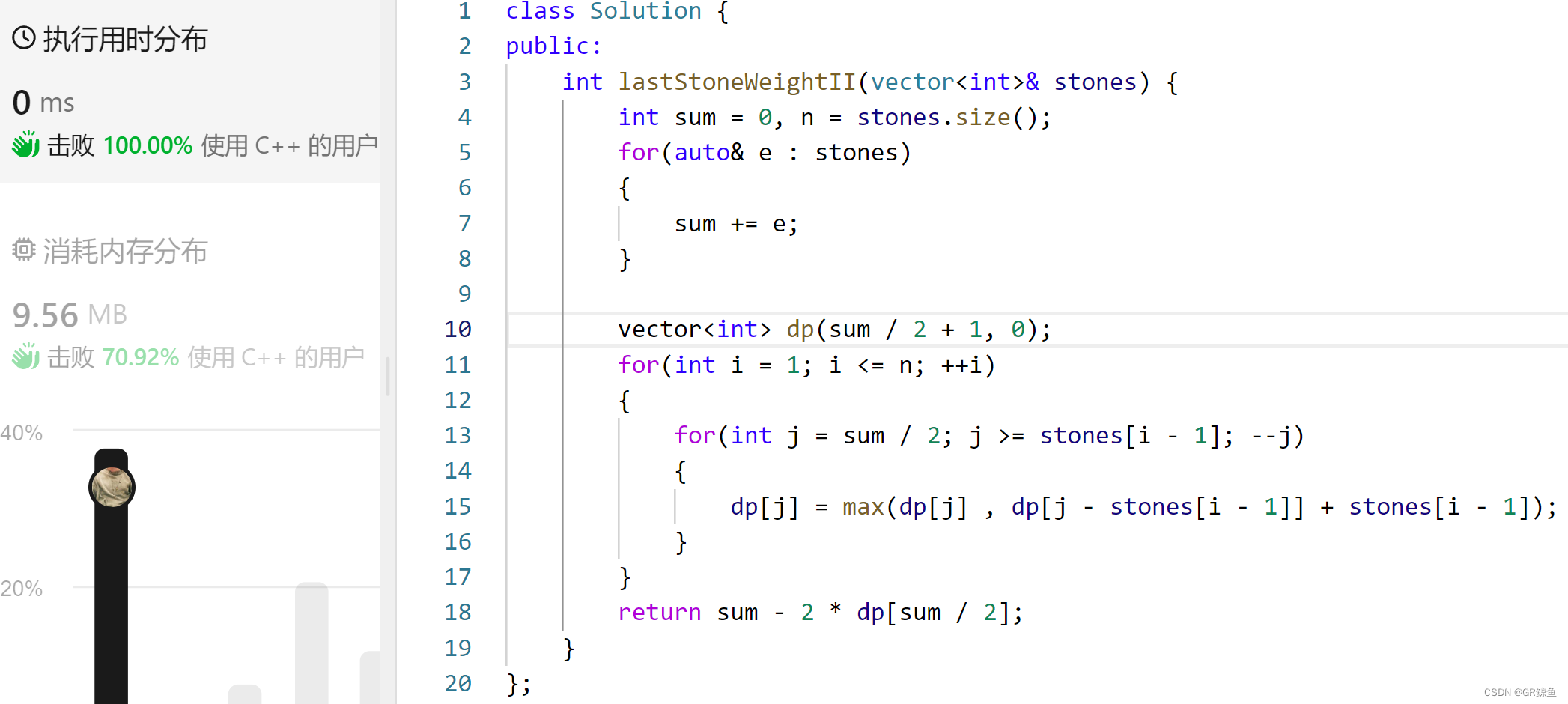
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0, n = stones.size();for(auto& e : stones){sum += e;}vector<int> dp(sum / 2 + 1, 0);for(int i = 1; i <= n; ++i){for(int j = sum / 2; j >= stones[i - 1]; --j){dp[j] = max(dp[j] , dp[j - stones[i - 1]] + stones[i - 1]) ;}}return sum - 2 * dp[sum / 2];}
};