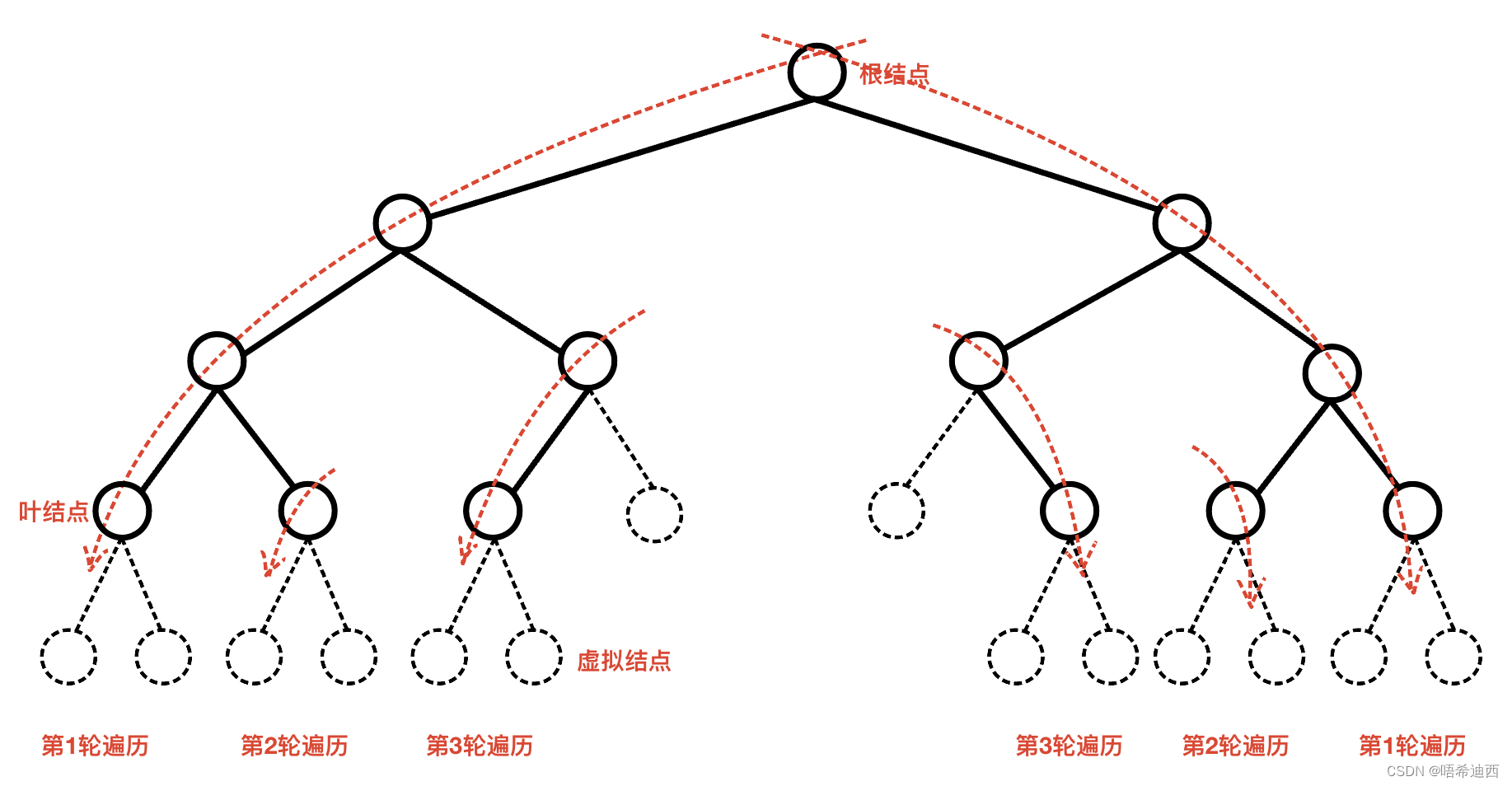
题目1:二叉树的前序遍历
链接:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void DFS_pre(TreeNode* ptr, vector<int>& result) {if(ptr == nullptr) return;result.push_back(ptr->val);DFS_pre(ptr->left, result);DFS_pre(ptr->right, result);}vector<int> preorderTraversal(TreeNode* root) {//个人尝试:递归求解//前序:中左右vector<int> result;DFS_pre(root, result);return result;}
};补充说明:对于二叉树的前中后续遍历,传入的指针参数只有一个
题目2:对称二叉树
链接:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool Compare_Left_And_Right(TreeNode* left, TreeNode* right) {//终止条件if(left == nullptr && right == nullptr) return true;if(left != nullptr && right == nullptr) return false;if(left == nullptr && right != nullptr) return false;if(left->val != right->val) return false; //比较中侧(这四个终止条件,都是对中侧的比较)bool outside = Compare_Left_And_Right(left->left, right->right); //比较外侧bool inside = Compare_Left_And_Right(left->right, right->left); //比较内侧return (outside && inside);}bool isSymmetric(TreeNode* root) {//自己尝试:递归法if(root == nullptr) return true;return Compare_Left_And_Right(root->left, root->right);}
};补充:对于这个题,递归函数体内部传入了两个指针参数
感悟:在做这个题之前,我一直以为递归算法只能指定一个遍历方向,但其实递归非常的强大,可以指定多个方向同时遍历;
(1)如果递归函数体只能传入一个指针参数,那么递归只能往同一个方向遍历;例如对二叉树前中后序的遍历,都是只有一个参数的递归,因此递归函数体的内部主逻辑中,只有对这一个参数的处理,而在递归函数体内部再一次调用递归函数体时,也是只能传入一个参数,那么这就导致我们只能往一个方向遍历;比如上个递归体中参数是左分支,那么当前这个递归体传入的参数必须是左分支的左分支,即都是往左进行的遍历;(否则一会往左递归,一会往右递归,就乱套了,没有了共同规则的约束)
(2)如果递归函数体可以传入两个指针参数,那么递归就可以往两个方向同时进行;例如对称二叉树这个题,我们想左子树往左遍历,右子树往右遍历,那么递归的参数必须有俩,一个遵循往左走, 一个遵循往右走,即两个参数往两个不同的方向走;
图解: