文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:收集树上所有苹果的最少时间
出处:1443. 收集树上所有苹果的最少时间
难度
6 级
题目描述
要求
给定一个有 n \texttt{n} n 个结点的无向树,结点编号为 0 \texttt{0} 0 到 n − 1 \texttt{n} - \texttt{1} n−1,有一些结点有苹果。通过树上的一条边需要花费 1 \texttt{1} 1 秒钟。计算从结点 0 \texttt{0} 0 出发收集所有苹果并回到结点 0 \texttt{0} 0 的最少时间的秒数并返回。
无向树的边由 edges \texttt{edges} edges 给出,其中 edges[i] = [a i , b i ] \texttt{edges[i] = [a}_\texttt{i}\texttt{, b}_\texttt{i}\texttt{]} edges[i] = [ai, bi],表示有一条边连接 a i \texttt{a}_\texttt{i} ai 和 b i \texttt{b}_\texttt{i} bi。除此以外,还有一个布尔数组 hasApple \texttt{hasApple} hasApple,其中 hasApple[i] = true \texttt{hasApple[i] = true} hasApple[i] = true 表示结点 i \texttt{i} i 有一个苹果,否则结点 i \texttt{i} i 没有苹果。
示例
示例 1:
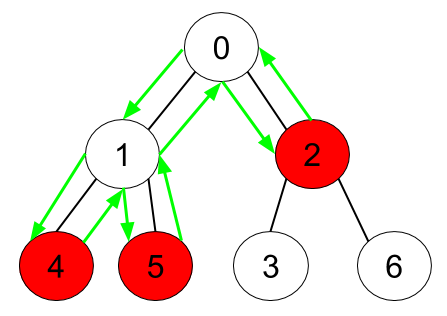
输入: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false] \texttt{n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]} n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
输出: 8 \texttt{8} 8
解释:上图展示了给定的树,其中红色结点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
示例 2:

输入: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false] \texttt{n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]} n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
输出: 6 \texttt{6} 6
解释:上图展示了给定的树,其中红色结点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
示例 3:
输入: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false] \texttt{n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]} n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
输出: 0 \texttt{0} 0
数据范围
- 1 ≤ n ≤ 10 5 \texttt{1} \le \texttt{n} \le \texttt{10}^\texttt{5} 1≤n≤105
- edges.length = n − 1 \texttt{edges.length} = \texttt{n} - \texttt{1} edges.length=n−1
- edges[i].length = 2 \texttt{edges[i].length} = \texttt{2} edges[i].length=2
- 0 ≤ from i , to i ≤ n − 1 \texttt{0} \le \texttt{from}_\texttt{i}\texttt{, to}_\texttt{i} \le \texttt{n} - \texttt{1} 0≤fromi, toi≤n−1
- from i < to i \texttt{from}_\texttt{i} < \texttt{to}_\texttt{i} fromi<toi
- hasApple.length = n \texttt{hasApple.length} = \texttt{n} hasApple.length=n
解法
思路和算法
这道题中的树使用无向边表示,规定根结点是结点 0 0 0,其余结点之间只能知道连通关系。为了得到相邻结点之间的父结点和子结点的关系,需要根据给定的边得到每个结点的相邻结点,然后从根结点开始遍历树。在确定所有相邻结点之间的父结点和子结点的关系之后,即可得到树的结构,包括每个结点的父结点和子结点,然后计算收集树上所有苹果的最少时间。
可以使用深度优先搜索得到树的结构。从根结点开始遍历,遍历过程中需要知道相邻结点之间的父结点和子结点的关系。由于和一个结点相邻的结点只有该结点的父结点和全部子结点,一种方法是在遍历过程中传入当前结点的父结点编号,在遍历与当前结点相邻的结点时跳过父结点,则可确保只会访问当前结点的子结点。
为了将收集苹果的时间降到最低,对于树中的每个苹果,应该考虑最短路径,即从根结点直接到达苹果所在结点的路径。当树中有多个苹果时,收集苹果的过程中应该避免重复路径,即同一条边最多在两个方向上各走一次。例如,示例 1 中收集树上所有苹果需要经过的边包括 [ 0 , 1 ] [0, 1] [0,1]、 [ 1 , 4 ] [1, 4] [1,4]、 [ 1 , 5 ] [1, 5] [1,5]、 [ 0 , 2 ] [0, 2] [0,2],共有 4 4 4 条边,最少时间的方案下每条边走 2 2 2 次,因此最少时间是 8 8 8。
基于上述分析,为了计算最少时间,需要计算收集树上所有苹果需要经过的最少边数,将边数乘以 2 2 2 即为最少时间。
计算过程中,为了避免重复计算,需要记录每个结点是否访问过,初始时只有根结点 0 0 0 被访问过。对于每个有苹果的结点,从该结点出发向根结点移动,将经过的每个结点(包括该结点本身)的状态都设为被访问过,当遇到一个已经访问过的结点时结束当前结点的移动。如果遇到一个已经访问过的结点 x x x,则从结点 x x x 到根结点的路径上的所有边都已经访问过,因此不应重复访问。
对于全部有苹果的结点计算结束之后,即可得到收集树上所有苹果需要经过的最少边数。
实现方面,可以在计算边数的同时计算最少时间,对于遍历到的每条边,将时间加 2 2 2。
代码
class Solution {List<Integer>[] adjacentNodes;int[] parents;boolean[] visited;public int minTime(int n, int[][] edges, List<Boolean> hasApple) {adjacentNodes = new List[n];for (int i = 0; i < n; i++) {adjacentNodes[i] = new ArrayList<Integer>();}for (int[] edge : edges) {int node0 = edge[0], node1 = edge[1];adjacentNodes[node0].add(node1);adjacentNodes[node1].add(node0);}parents = new int[n];Arrays.fill(parents, -1);dfs(0, -1);visited = new boolean[n];visited[0] = true;int time = 0;for (int i = 0; i < n; i++) {if (hasApple.get(i)) {time += getTime(i);}}return time;}public void dfs(int node, int parent) {List<Integer> adjacent = adjacentNodes[node];for (int next : adjacent) {if (next == parent) {continue;}parents[next] = node;dfs(next, node);}}public int getTime(int node) {int time = 0;while (!visited[node]) {visited[node] = true;node = parents[node];time += 2;}return time;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是树的结点数。深度优先搜索的过程中每个结点访问一次,计算最少时间的过程中每条边最多遍历一次,共有 n n n 个结点和 n − 1 n - 1 n−1 条边,因此时间复杂度是 O ( n ) O(n) O(n)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是树的结点数。空间复杂度包括存储相邻结点信息的空间、记录每个结点的父结点信息的空间和递归调用的栈空间,存储相邻结点信息的空间和记录每个结点的父结点信息的空间是 O ( n ) O(n) O(n),递归调用的栈空间在最坏情况下是 O ( n ) O(n) O(n),因此空间复杂度是 O ( n ) O(n) O(n)。