排序之归并排序-编程知识

排序之归并排序

代码

先上代码，根据代码将归并排序的整个过程。

class Solution {public int[] sortArray(int[] nums) {int[] tmp = new int[nums.length];merge(nums, 0, nums.length - 1, tmp);return nums;}private void merge(int[] nums, int left, int right, int[] tmp){if(left == right) return;int mid = left + (right - left) / 2;merge(nums, left, mid, tmp);merge(nums, mid + 1, right, tmp);sort(nums, left, mid, right, tmp);}private void sort(int[] nums, int left, int mid, int right, int[] tmp){int l = left;int r = mid + 1;int idx = 0;while(l <= mid && r <= right){if(nums[l] < nums[r]){tmp[idx++] = nums[l++];}else{tmp[idx++] = nums[r++];}}while(l <= mid){tmp[idx++] = nums[l++];}while(r <= right){tmp[idx++] = nums[r++];}int pivot = left;idx = 0;while(pivot <= right){nums[pivot++] = tmp[idx++];}}
}

过程

        先整个数组。
请添加图片描述
        归并排序会借助一个数组辅助排序，用tmp表示，待排序数组，用nums表示。思想是自顶向下分，自底向上排。上述代码关键就是两个方法，一个是merge方法，一个是sort方法。
        首先找到数组的中间结点，为5。根据5，划分为数组的左侧[8, 12, 1, 5]，数组的右侧[7, 9, 6]。左侧和右侧数组继续划分，如下图所示，直至left和right指针相等。
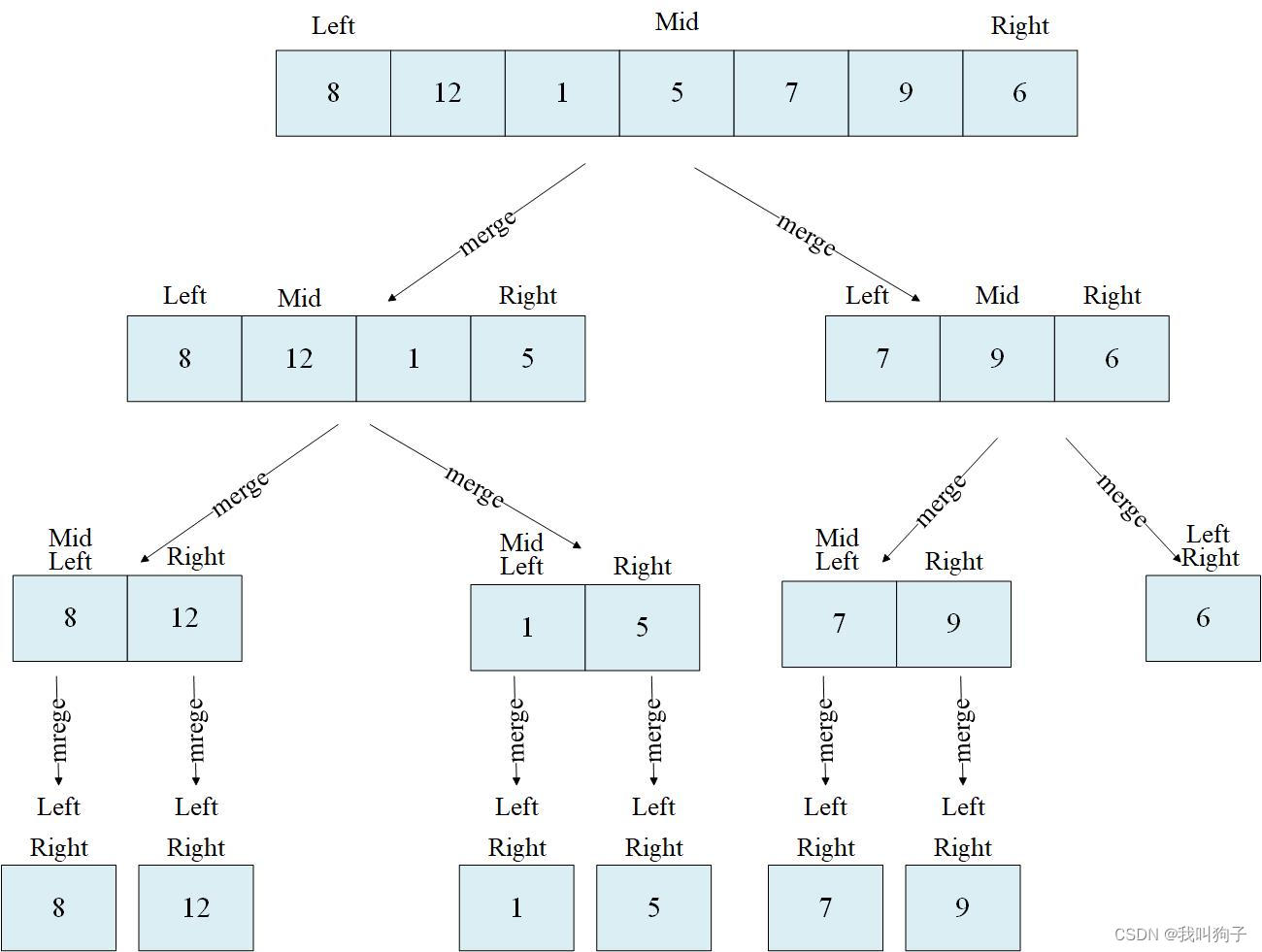
请添加图片描述
        划分完之后，merge有两种情况，一种情况如最后一个结点8，进入merge方法后，由于left == right，使得merge方法直接return；即仅有一个结点时，merge方法仅经过一条判断语句，就直接返回。还有一种情况是比如划分到[8, 12]时，进入merge方法，划分为[8]和[12]，递归进入下一个merge方法，由于left==right，导致[8]和[12]的两个merge方法仅经过一条判断语句，直接return。回到[8,12]这个merge方法继续执行，即进入sort方法。
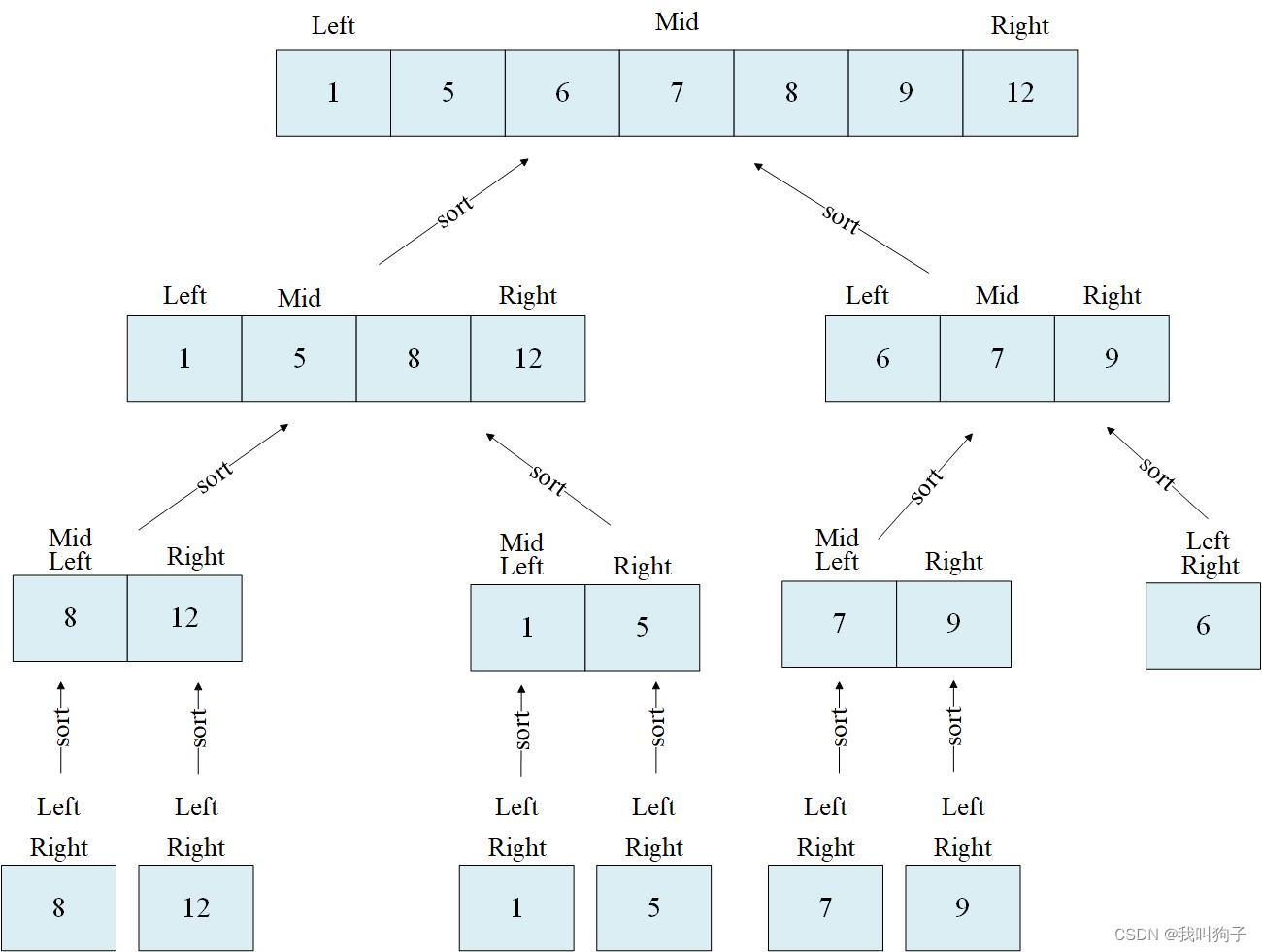
        [8,12]进入sort方法，l等于left，等于8，r等于mid+1,等于12。比较8和12，8小，将tmp数组的第一个元素赋值为8，l++，l++后，大于了mid，跳出第一个while循环，进入下一个循环，由于l大于mid，不进入第二个while循环，此时r还是小于right，会进入第三个循环，将tmp数组的第二个元素赋值为12。此时就完成了该数组中每个数字之间的相对顺序。将排好序的tmp数组，赋值给nums数组。
        再看一个例子，[8, 12, 1,5]，l指向8，r指向mid+1,为1，此时，比较8和1的大小，1小，tmp数组第一个元素赋值为1，r++,指向5，比较8和5的大小，5小，将tmp数组的第二个元素赋值为5，r++，r大于right，跳出第一个while循环，第二个while循环，判断l是否小于mid，显然l指向为8，小于mid，将tmp中第三个元素和第四个元素赋值为8和12，跳出第二个while循环，此时r大于right，不会进入第三个while循环。最后将排序好的tmp的数组赋值给nums。
        在sort方法中，[left,mid]和[mid+1,right]两个数组一定满足从小到大的顺序，sort方法解决的问题是将两个升序数组借助一个tmp数组实现从小到大的排序问题。最后将tmp数组中的值赋值给原nums数组，就可以实现nums数组中[left,right]这个区间从小到大的排序。可以做一下合并两个有序数组。原理是一模一样的。
请添加图片描述