代码随想录阅读笔记-回溯【分割回文串】-编程知识

题目

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]

思路

本题这涉及到两个关键问题：

切割问题，有不同的切割方式
判断回文

相信这里不同的切割方式可以搞懵很多同学了。

这种题目，想用for循环暴力解法，可能都不那么容易写出来，所以要换一种暴力的方式，就是回溯。

一些同学可能想不清楚回溯究竟是如何切割字符串呢？

我们来分析一下切割，其实切割问题类似组合问题。

例如对于字符串abcdef：

组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个.....。
切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段.....。

感受出来了不？

所以切割问题，也可以抽象为一棵树形结构，如图：

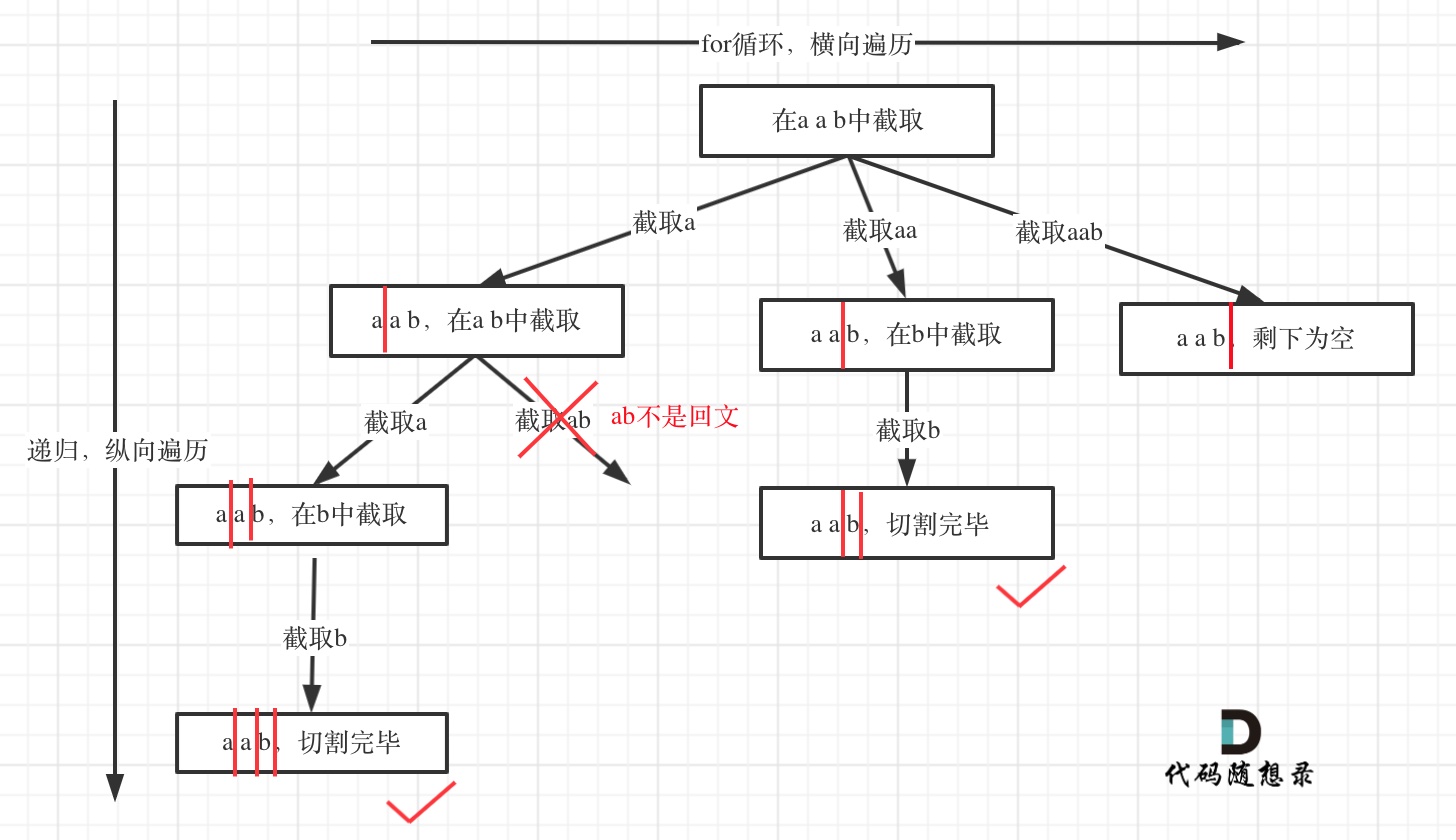
131.分割回文串

递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

此时可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。

回溯三部曲

1、递归函数参数

全局变量数组path存放切割后回文的子串，二维数组result存放结果集。（这两个参数可以放到函数参数里）本题递归函数参数还需要startIndex，因为切割过的地方，不能重复切割，和组合问题也是保持一致的。

vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex) {

2、递归函数终止条件

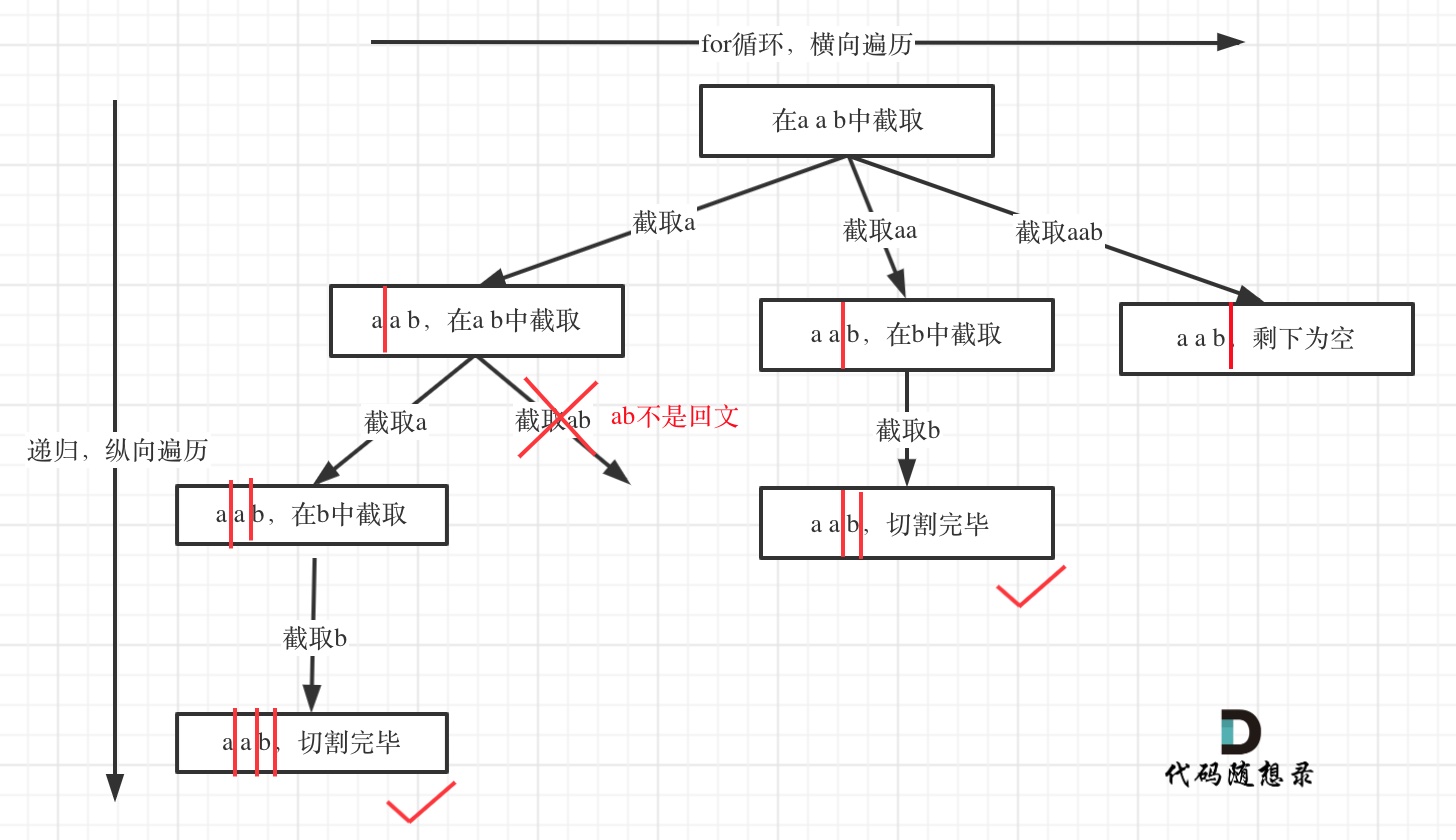
131.分割回文串

从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。

那么在代码里什么是切割线呢？

在处理组合问题的时候，递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线。

所以终止条件代码如下：

void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}
}

3、单层搜索的逻辑

来看看在递归循环中如何截取子串呢？

在for (int i = startIndex; i < s.size(); i++)循环中，我们定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。

首先判断这个子串是不是回文，如果是回文，就加入在vector<string> path中，path用来记录切割过的回文子串。

代码如下：

for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else {                // 如果不是则直接跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back();        // 回溯过程，弹出本次已经添加的子串
}

注意切割过的位置，不能重复切割，所以，backtracking(s, i + 1); 传入下一层的起始位置为i + 1。

判断回文子串

最后我们看一下回文子串要如何判断了，判断一个字符串是否是回文。

可以使用双指针法，一个指针从前向后，一个指针从后向前，如果前后指针所指向的元素是相等的，就是回文字符串了。

那么判断回文的C++代码如下：

 bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}

整体代码如下：

class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) {   // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else {                                // 不是回文，跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串，这里会有人把参数写成startIndex+1，一定要注意，这里i代表树结构中每一层中的切割字符串的终止位置，startIndex代表起始位置，所以开始回溯（纵向延伸）时是需要从终止位置的下一个开始，不然就会将已经处理的字符在回溯中重复处理path.pop_back(); // 回溯过程，弹出本次已经添加的子串}}bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;}
};

时间复杂度: O(n * 2^n)
空间复杂度: O(n^2)

优化

上面的代码还存在一定的优化空间, 在于如何更高效的计算一个子字符串是否是回文字串。上述代码isPalindrome函数运用双指针的方法来判定对于一个字符串s, 给定起始下标和终止下标, 截取出的子字符串是否是回文字串。但是其中有一定的重复计算存在:

例如给定字符串"abcde", 在已知"bcd"不是回文字串时, 不再需要去双指针操作"abcde"而可以直接判定它一定不是回文字串。

具体来说, 给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。

大家如果熟悉动态规划这种算法的话, 我们可以高效地事先一次性计算出, 针对一个字符串s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤.

具体参考代码如下:

class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串vector<vector<bool>> isPalindrome; // 放事先计算好的是否回文子串的结果void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome[startIndex][i]) {   // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else {                                // 不是回文，跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程，弹出本次已经添加的子串}}void computePalindrome(const string& s) {// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串 isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小for (int i = s.size() - 1; i >= 0; i--) { // 需要倒序计算, 保证在i行时, i+1行已经计算好了for (int j = i; j < s.size(); j++) {if (j == i) {isPalindrome[i][j] = true;}else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}}}}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();computePalindrome(s);backtracking(s, 0);return result;}
};