15. 三数之和 - 力扣(LeetCode)

先确定一个数t,对于剩下的两个数,要求两数之和为t的负数
三数之和就退化成了两数之和,两数之和可以用双指针
先排序,左右两个指针,指向的数之和大于目标值,则r–,反之l++
两数之和为目标值的组合可能不止一对,所以双指针需要走到l == r时停止
根据题目要求,确定两数之和为目标值后,两个指针都需要跳过相同的数,才能继续走
同时,每次双指针的目标值也不能相同
最后,左指针不能从数组的0下标开始,应该从t的后一位开始。这样就能保证每次枚举的三元组都是从小到大排序,不会出现重复的情况
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> ans;for (int i = 0; i < nums.size(); ++ i){if (i && nums[i] == nums[i - 1]) continue;int l = i + 1, r = nums.size() - 1;int t = -nums[i];while (l < r){if (l == i) { l ++ ; continue; }if (r == i) { r -- ; continue; }if (nums[l] + nums[r] < t) l ++ ;else if (nums[l] + nums[r] > t) r -- ;else {ans.push_back({nums[i], nums[l], nums[r]});l ++ , r -- ;while (l < r && nums[l] == nums[l - 1]) l ++ ;while (l < r && nums[r] == nums[r + 1]) r -- ;}}}return ans;}
};
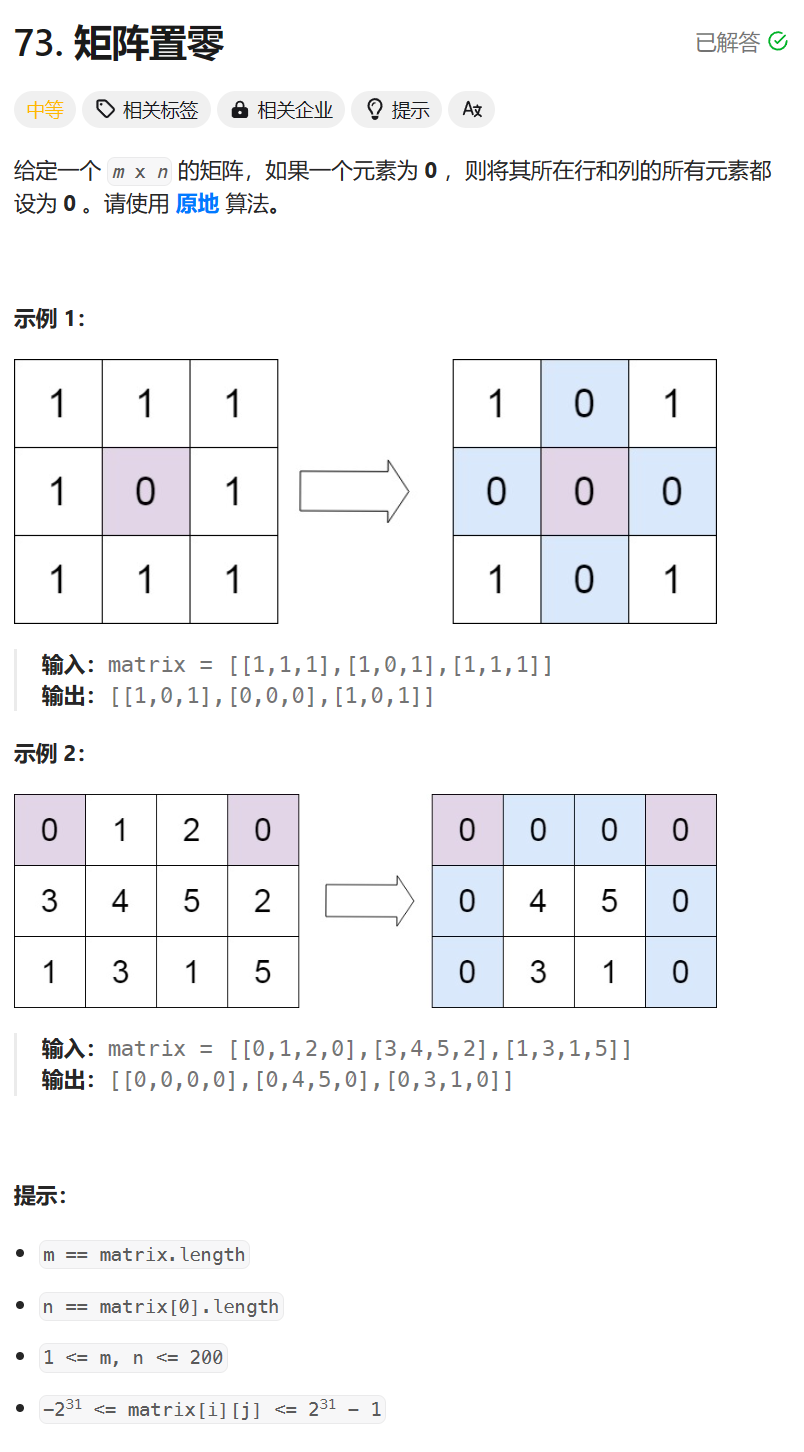
73. 矩阵置零 - 力扣(LeetCode)
用两个数组维护哪些行/哪些列出现了0,如果第i行/列出现了0,将第i个元素置0
直接将原数组的第0行的第0列作为这两个数组,此时直接修改第0行/第0列的元素为0不会影响答案
问题是:需要确定第0行/第0列是否已经存在0,若存在则需要将整行/整列置0
所以需要使用bool变量先记录这两个数组是否存在0
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int row = matrix.size(), col = matrix[0].size();bool r = false, c = false;for (int i = 0; i < col; ++ i) if (!matrix[0][i])r = true;for (int i = 0; i < row; ++ i)if (!matrix[i][0])c = true;for (int i = 1; i < row; ++ i)for (int j = 1; j < col; ++ j)if (!matrix[i][j])matrix[i][0] = 0, matrix[0][j] = 0;for (int i = 1; i < row; ++ i)for (int j = 1; j < col; ++ j)if (!matrix[i][0] || !matrix[0][j])matrix[i][j] = 0;for (int i = 0; r && i < col; ++ i)matrix[0][i] = 0;for (int i = 0; c && i < row; ++ i)matrix[i][0] = 0;}
};