目录
- 【数据结构】遍历二叉树(递归和非递归遍历的先序、中序和后序遍历、层次遍历法)
- 一、递归算法
- 先(根)序的遍历算法
- 中(根)序的遍历算法
- 后(根)序的遍历算法
- 二、非递归算法
- 层次遍历
- 先序遍历非递归算法
- 中序遍历非递归算法
- 后序遍历非递归算法
【数据结构】遍历二叉树(递归和非递归遍历的先序、中序和后序遍历、层次遍历法)
采用二叉链表的形式储存
结点结构 [lchild,data,rchild]
特点:二叉链表找子孙结点容易,找祖先结点麻烦。
typedef struct BiTNode { char data; struct BiTNode *lchild, *rchild; //左右子树根结点地址
} BiTNode, *BiTree;
一、递归算法
递归算法书写简单,但是效率低。
先(根)序的遍历算法
先序遍历(递归定义 递归结束的条件就是:空树 )
- 若二叉树为空树,则空操作;
- 否则,(1)访问根结点;(2)先序遍历左子树;(3)先序遍历右子树。
先序遍历的递归算法:
//先序遍历 递归访问每一个结点
void xxbl(BiTree T){if(T){//递归调用的结束条件printf("%c",T->data);//访问结点xxbl(T->lchild);//遍历左子树xxbl(T->rchild);//遍历右子树}
}
中(根)序的遍历算法
- 若二叉树为空树,则空操作;
- 否则,(1)中序遍历左子树;(2)访问根结点;(3)中序遍历右子树。
中序遍历的递归算法:
void zxbl(BiTree T)
{if (T) {zxbl(T->lchild); printf("%c",T->data); zxbl(T->rchild);}
}
后(根)序的遍历算法
- 若二叉树为空树,则空操作;
- 否则,(1)后序遍历左子树;(2)后序遍历右子树;(3)访问根结点。
void hxbl(BiTree T)
{if(T){hxbl(T->lchild); hxbl(T->rchild); printf("%c",T->data);}
}
二、非递归算法
- 用循环队列实现二叉树的按层次遍历
- 使用栈 来实现 先保存 后 访问
层次遍历
从根节点开始,先访问第一层的结点,在访问第二层的结点。
特点:自顶向下,从左到右的访问次序。
借用 队列(循环队列) 来实现层次遍历的功能,所有要访问的结点都存放在队列中。
- 初始时若二叉树非空,则只需要知道要访问的第一个结点为根结点。
- 只要队列不空,说明队列中存有要访问的结点,则取队首结点访问,并将其非空左右孩子依次插入队列中。

算法代码示例:
//层次遍历算法
#define MAX 100
void LevelTrave(BiTree T){BiTree Q[MAX],p;//用循环队列实现二叉树的按层次遍历int f=r=0;//队列 队首和队尾指针if(T==NULL) return;Q(r++)=T;// 根节点入队while(f!=r){p=Q[f++];//出队printf("%c",p->data);if(p->lchild){if(r>=MAX){printf("overflow");exit(0);}Q[r++]=p->lchild;}if(p->rchild){if(r>=MAX){printf("overflow");exit(0);}Q[r++]=p->rchild;}}
}
先序遍历非递归算法
先序遍历非递归算法的实现:访问根节点后,在访问左子树之前,先将其非空右子树的地址入栈(保存)。

采用顺序栈来存放访问过的结点右子树:
#define MAX 10000
typedef struct{BiTree data[MAX];int top;
}SeqStack;
void PreorderTraverse(BiTree T){//T为二叉树的根结点SeqStack s;//新建一个 栈BiTree p;s.top=-1; //栈顶指针p = T;//while(p){while(p){//访问左子树printf("%c",p->data); //访问p结点if(p->rchild) {//将p结点的非空右孩子入栈保存if(s.top==MAX-1) exit (0);//栈溢出else s.data[++s.top]=p->rchild;//入栈}p =p->lchild; //访问p的左孩子 }if (s.top!=-1) p=s.data[s.top--];//出栈}
}中序遍历非递归算法
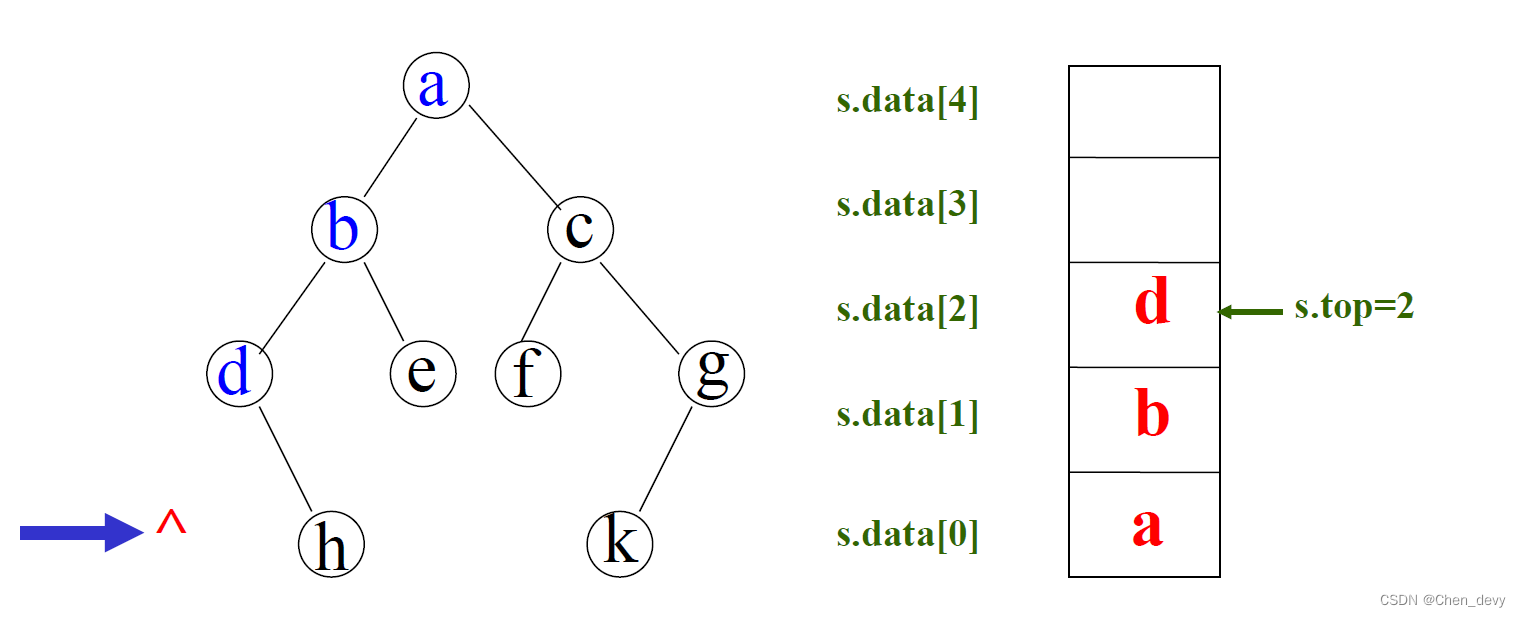
- 基本思想:访问根结点的左子树前,应保存其根结点,以便左子树访问结束后,访问根和根的右子树
- 图中a结点先于b结点被保存,但是其访问要在b及b的右子树被访问后进行----先保存后访问----先进后出----借助栈来实现
void InorderTraverse(BiTree T){//中序遍历根结点为T的二叉树SeqStack s; BiTree p;s.top=-1; p = T;while(p||(s.top!=-1)){ //while(p){if(s.top==MAX-1) exit (0);s.data[++s.top]=p; p =p->lchild;// 一直去访问左子树 同时将结点入栈//向左下走一直走到头}if (s.top!=-1){p=s.data[s.top--];//根节点出栈printf("%c",p->data);p = p->rchild; //访问该根节点的右子树}}
}
后序遍历非递归算法
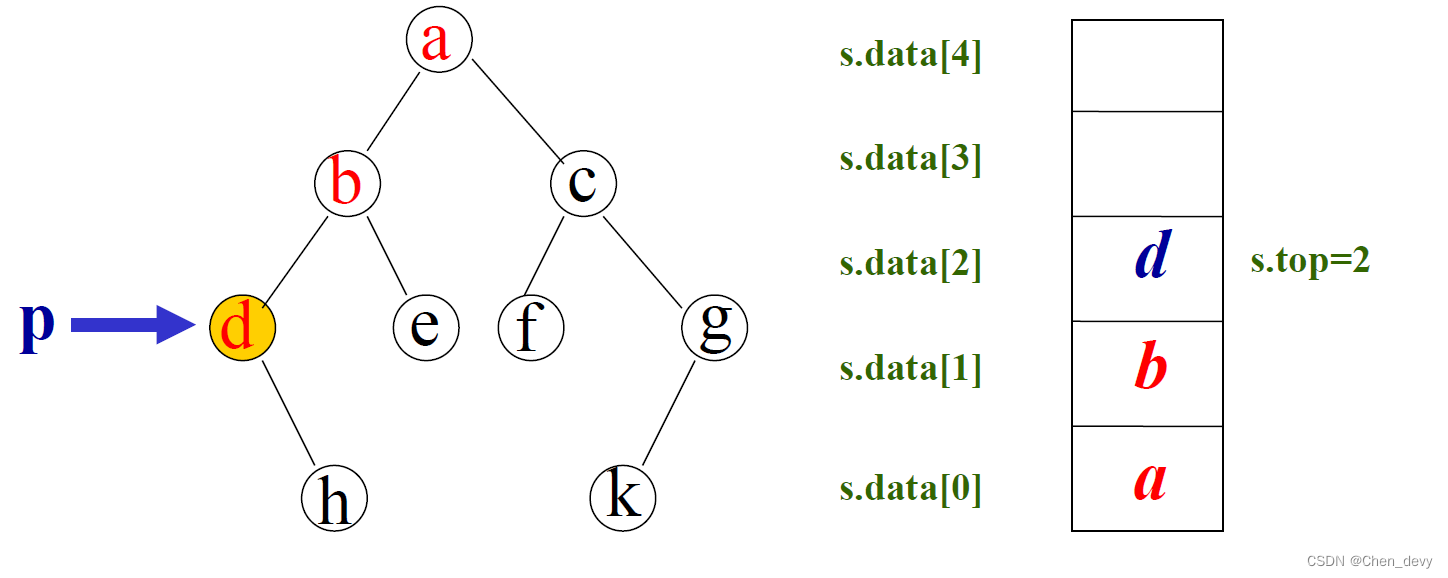
- 后序遍历非递归算法的实现:访问根结点的左子树前,应保存其根结点,以便左子树访问结束后,访问根的右子树和根
- 图中a结点先于b结点被保存,但是其访问要在b及其右子树被访问后进行----先保存后访问----先进后出----借助栈实现
只有在其左、右子树被访问后才能被访问(需要标记 定义一个flag 来标记其左右子树是否都被访问过)
#define MAX5
typedef struct{BiTree q;int flag;
}dataelem;
//q存放的是遍历操作访问到的一棵子树的根节点
//flag=0代表目前是在访问q结点的左子树,flag=1代表目前是在访问q结点的右子树
typedef struct{
dataelem data[MAX];
int top;//栈顶指针
}SeqStack2;
代码示例(!!!):
void postorder(BiTree T){SeqStack2 s;s.top=-1;p=T;do{while(p!=NULL){if(s.top==MAX-1) exit (0);//栈溢出s.data[++s.top].q=p; s.data[s.top].flag=0; p=p->lchild;//一直向左下访问 }while((s.top>-1)&&(s.data[s.top].flag==1)){ //p=s.data[s.top--].q; printf(“%c”,p->data); }if(s.top>-1){s.data[s.top].flag=1;//标记 此时开始访问 其右子树p=s.data[s.top].q; p=p->rchild;}}while(s.top>-1);
}
感谢阅读!!!
- 树与二叉树知识点文章: 【数据结构】树与二叉树(递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法)
- 二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用(求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子)
- 二叉树遍历算法的应用: 【数据结构】树与森林(树的存储结构、森林与二叉树的转化、树与森林的遍历)