关联规则挖掘（一）-编程知识

一、关联规则的概念

（一）基本概念

事务数据库（Transaction Database） $T=\{t_1,t_2,…,t_n\}$ ，也称为交易数据库中的关联规则挖掘问题可描述如下：

设 $I=\{i_1,i_2,…,i_m\}$ 为一个项目集合 (Set of Items, 项集)，其中 $i_1,i_2,…,i_m$ 称为项目 (item, 项)。在超市的交易数据仓库中，每个项ik代表一种商品的编号或名称，为计算方便假设 $I$ 中的项已按字典序排序。

$T$ 中的每个事务 $t_j$ 都是I的一个子集，即 $t_j \subseteq I (j=1,2,…,n)$ 。在超市等交易数据仓库中， $t_j$ 就代表某个顾客一次购买的所有商品编号或商品名称。

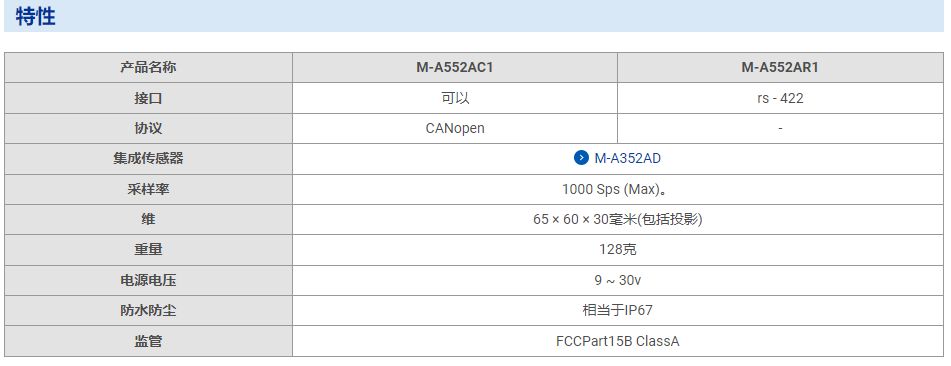
例 8-1 对表8-1所示的交易数据库记录，请给出项集和其中的事务。

在这里插入图片描述
解：交易数据库涉及 $a, b, c, d$ 等4个项，即项集 $I=\{a,b,c,d\}$ 且其中的项已经按字典序排序。每一个项就代表一种商品，比如 $a$ 可表示面包， $b$ 表示牛奶等。交易数据库可表示为 $T=\{t_1, t_2, t_3\}$ ，其中 $t_1=\{a, b\}$ ， $t_2=\{b, c, d\}$ ， $t_3=\{b, d\}$ ，且它们都是项集 $I$ 的子集，且按照字典序排序。

定义 8-1 若 $X\subseteq I$ 且 $k = ∣ X ∣$ ，则称 $X$ 为 k-项集，将包含 $X$ 的事务数 $X\subseteq t\in T}|$ 称为 $X$ 在事务数据库 $T$ 上的支持数，并将 $SptN (X)$ 与 $∣ T ∣$ 的比值称为 $X$ 在 $T$ 上的支持度 (Support)，记作 $Support(X)=|\{ t | X\subseteq t\in T\}| / | T | \tag{8-1}$ 显然，一个 k-项集 $X$ 的支持度 $(X)\in [0,1]$ 。

对于例8-1所示的交易数据库 $T$ ，设有项集 $X=\{b,d\}$ ，则 $SptN (X) = 2$ ， $S u pp or t (X) = 2/3$ 。

定义 8-2 若指定 $MinS\in(0,1)$ 作为刻画支持度是否符合用户期望的阈值，则 $M in S$ 称为最小支持度，并将 $MinSptN=MinS\times|T|$ 称为最小支持数，即 $M in SptN$ 是最小支持度 $M in S$ 与事务数据库记录数的乘积。

定义 8-3 设 $X\subseteq I$ ， $Y\subseteq I$ 且 $X\cap Y=\phi$ ，称形如 $X\Rightarrow Y$ 的蕴涵式为关联规则 (Association Rule)，其中 $X$ 和 $Y$ 分别称为关联规则的先导 (Antecedent) 和后继 (Consequent)。

定义 8-4 设 $X\subseteq I$ ， $Y\subseteq I$ 且 $X\cap Y=\phi$ ，令 $Z=X\cup Y$ ，则称 $S u pp or t (Z)$ 为关联规则 $X\Rightarrow Y$ 的支持度，记作 $(X\Rightarrow Y)$ 。

从定义8-1和8-4可知，关联规则 $X\Rightarrow Y$ 在事务数据库 $T$ 上的支持度，就是 $T$ 中同时包含 $X$ 和 $Y$ 的事务在 $T$ 中所占的百分比，即： $(X\Rightarrow Y)=包含X\cap Y的事务数/ |T|\tag{8-2}$ 对于例8-1的交易数据库 $T$ ，若令 $X=\{b,c\},Y=\{d\}$ ，则
$(X\Rightarrow Y)= Support (\{b,c\} \Rightarrow \{d\})=Support (b,c,d)=1/3$ 由此可知，在购物篮分析中， $X\Rightarrow Y$ 的支持度也可以表示为 $(X\Rightarrow Y)=\frac{同时购买商品X和Y的交易数}{总交易数}\tag{8-3}$

定义 8-5 设 $X\subseteq I$ 和给定的最小支持度 $M in S$ ，若 $Support(X)\geq MinS$ ，则称 $X$ 为频繁项集 (Frequent Item Sets)。若 $k = ∣ X ∣$ ，则称 $X$ 为频繁 k-项集。

对例8-1交易数据库 $T$ ，若最小支持度 $M in S = 0.6$ ，对项集 $X=\{b,d\}$ ，因为 $(X)=2/3\geq 0.6$ ，即 $X=\{b, d\}$ 是个频繁项集，且是频繁2-项集。

定义 8-6 设 $X_1,X_2,\cdots,X_r$ 是 $T$ 上关于最小支持度 $M in S$ 的所有频繁项集，称 $X_q$ 为一个最大频繁项目集，若对任意 $p(p=1,2,\cdots,r；p\neq q)$ 都有 $X_q\not\subset X_p$ 。

因此， $X_q$ 为最大频繁项集的充分必要条件是， $X_q$ 不是其它任何频繁项集的子集。显然， $T$ 上的最大频繁项集通常不唯一。

定义 8-7 关联规则 $X\Rightarrow Y$ 在 $T$ 上的置信度 (Confidence)，定义为 $Confidence(X\Rightarrow Y) = Support (X\cup Y )/ Support (X)=SptN (X\cup Y )/ SptN(X)$

例 8-2 对例8-1的交易数据库 $T$ ，令 $X=\{b,c\},Y=\{d\}$ ，试求其置信度。

解：由于 $(X\cup Y)=Support(\{b,c,d\})=1/3$ ，而 $Support(X)= Support\{b,c\}=1/3$ ，所以 $Confidence(X\Rightarrow Y) = Support (X\cup Y )/ Support (X)=1$

定义 8-8 若 $MinC\in(0,1)$ 且指定为刻画置信度的阈值，则称 $M in C$ 为最小置信度。

定义 8-9 对于给定的最小支持度 $M in S$ 和最小置信度 $M in C$ ，如果有 $Support(X\Rightarrow Y)\geq MinS，Confidence(X\Rightarrow Y)\geq MinC$ 则称 $X\Rightarrow Y$ 为强关联规则 (Strong Association Rule)。

关联规则挖掘就是按用户指定最小支持度 $M in S$ 和最小置信度 $M in C$ ，从给定的事务数据库 $T$ 中寻找出所有强关联规则的过程。

（二）项集的性质

Agrawal 等人在研究事务数据库关联规则挖掘的过程中，发现了关于项集的两个基本性质，并在关联规则挖掘中被广泛应用。

定理 8-1 (频繁项集性质1)：如果 $X$ 是频繁项集，则它的任何非空子集 $X^{'}$ 也是频繁项集。即频繁项集的子集必是频繁项集

定理 8-2 (频繁项集性质2)：如果 $X$ 是非频繁项集，那么它的所有超集都是非频繁项集。即非频繁项集的超集也是非频繁项集。

二、关联规则的Apriori算法

Apriori 算法是 Agrawal 等学者提出的关联规则的经典挖掘算法，在关联规则挖掘领域具有很大影响力。算法名称源于它使用了关于项集的两个性质，即定理8-1和8-2等先验 (Apriori) 知识。
Apriori算法在具体实现时，将关联规则的挖掘过程分为如下两个基本步骤。

1、发现频繁项集

根据用户给定的最小支持度 $M in S$ ，寻找出所有的频繁项集，即满足支持度 $S u pp or t$ 不低于 $M in S$ 的所有项集。由于这些频繁项集之间有可能存在包含关系，因此，我们可以只关心所有的最大频繁项集，即那些不被其它频繁项集所包含的所有频繁项集。

2、生成关联规则

根据用户给定的最小可信度 $M in C$ ，在每个最大频繁项集中，寻找置信度 $C o n f i d e n ce$ 不小于 $M in C$ 的关联规则。

（一）发现频繁项集

如果 $∣ I ∣ = m$ ，则 $I$ 总共有 $2 m - 1$ 个非空的子集。若 $∣ T ∣ = n$ ，则对于每一个事务 $t_j$ 都要检查它是否包含这 $2 m - 1$ 个子集，其时间复杂性为 $O(n2^m)$ 。当 $m$ 很大时，关联规则挖掘的时间开销往往是巨大的。

发现频繁项集需引入以下有关概念和符号。

（1）候选频繁项集：最有可能成为频繁项集的项目集。
（2） $C_k$ ：所有候选频繁 k-项集的集合；
（3） $L_k$ ：所有频繁 k-项集构成的集合；
（4） $c_m^k$ ： $I$ 中所有 k-项集的集合；

显然， $C_1$ 和 $L_1$ 的计算比较容易，只要扫描事务数据库 $T$ 很容易找出其中的所有候选1-项集以及判断它们是否为频繁1-项集即可。

根据 “频繁项集的子集必为频繁项集” 这一性质，可利用频繁k-项集的集合 $L_k$ ，来构造所有候选 (k+1)-项目集的集合 $C_{k+1}$ ，再通过扫描数据库，从 $C_{k+1}$ 中找出频繁 (k+1)-项集的集合 $L_{k+1}(k=1,2,\cdots,m-1)$ 。

从前面的分析可知 $L_k\subseteq C_k\subseteq c_m^k(k=1,2,\cdots,m)$ 。

因此，要寻找所有频繁 k-项集的集合 $L_k$ ，只需计算候选频繁 k-项集的集合 $C_k$ 中每个项集的支持度，而不必计算 $I$ 中所有 k-项集的支持度，这在一定程度上减少了算法的计算量。

根据以上分析，我们可以得到 Apriori 算法第一部分：

算法8-1： Apriori算法之频繁项集发现算法
输入：项集 $I$ ，事务数据库 $T$ ，最小支持数 $M in SptN$
输出：所有频繁项集构成的集合 $L$
（1）求 $L_1$ ：① 通过扫描数据库 $T$ ，找出所有1-项集并计算其支持数作为候选频繁1-项集 $C_1$ ；
② 从 $C_1$ 中删除低于 $M in SptN$ 的元素，得到所有频繁1-项集所构成的集合 $L_1$ ；
（2）FOR $3,\cdots$
（3）连接：将 $L_k$ 进行自身连接生成一个候选频繁 $k + 1$ 项集的集合 $C_{k+1}$ ，其连接方法如下：对任意 $p,q\in L_k$ ，若按字典序有 $p=\{p_1, p_2,\cdots, p_{k-1}, p_k\}，q=\{p_1, p_2,\cdots, p_{k-1}, q_k\}$ 且满足 $p_k<q_k$ ，则把 $p, q$ 连接成 $k + 1$ 项集，即将 $p\oplus q=\{p_1, p_2,\cdots, p_{k-1}, p_k, q_k\}$ 作为候选 (k+1)-项集 $C_{k+1}$ 中的元素。
（4）剪枝：删除 $C_{k+1}$ 中明显的非频繁 (k+1)-项集，即当 $C_{k+1}$ 中一个候选 (k+1)-项集的某个 k-项子集不是 $L_k$ 中的元素时，则将它从 $C_{k+1}$ 中删除。
（5）算支持度：通过扫描事务数据库 $T$ ，计算 $C_{k+1}$ 中各个元素的支持数。
（6）求 $L_{k+1}$ ：剔除 $C_{k+1}$ 中低于最小支持数 $M in SptN$ 的元素，即得到所有频繁 (k+1)-项集构成的集合 $L_{k+1}$ 。
（7）若 $L_{k+1}=\varnothing$ ，则转第（9）步
（8）END FOR
（9）令 $L=L_2\cup L_3\cup\cdots\cup L_k$ ，并输出 $L$ 。

例 8-3 对表8-2所示的交易数据库，其项集 $I=\{a,b,c,d,e\}$ ，设最小支持度 $M in S = 0.4$ ，请找出所有的频繁项目集。

在这里插入图片描述

解：因支持度 $M in S = 0.4$ ，事务数据库有5条记录，即最小支持数 $M in SptN = 2$ 。

算法（1）求 $L_1$ ：扫描事务数据库，可得候选频繁1-项集及其支持数计算结果。

在这里插入图片描述
第一轮循环：对 $L_1$ 执行算法的（3）至（6）步。

算法（3）连接：由 $L_1$ 自身连接生成候选频繁2-项集的集合 $C_2$ ，其结果由表8-4左侧第1列给出，且已按字典序排序。 ${a\}$ 与 ${b\}, \{c\}, \{d\} , \{e\}$ 分别连接生成 ${a,b\}, \{a,c\}, \{a,d\}$ 和 ${a,e\}$ 。 ${b\}$ 与 ${c\}, \{d\}, \{e\}$ 分别连接生成 ${b,c\}, \{b,d\}, \{b,d\}$ 。……

在这里插入图片描述

算法（4）剪枝：由于 $I$ 中所有1-项集都是频繁的，因此 $C_2$ 无需进行剪枝过程。

算法（5）算支持数：扫描数据库，计算其支持数。

算法（6）求 $L_2$ ：删除支持数小于等于2的候选2-项集，最终得到所有的频繁2-项集。

算法（7） $L_2≠\varnothing$

第二轮循环：对 $L_2$ 执行算法的（3）至（6）步获得 $L_3$ 。 $SptN(\{d,e\})=1$ , ${b, d, e\}$ 被剪枝。

在这里插入图片描述

第三轮循环：对 $L_3$ 执行算法的（3）至（6）步获得 $L_4$ 。

在这里插入图片描述

第四轮循环：由于 $L_4$ 仅有一个频繁4-项集，故已不能生成候选频繁5-项集 $C_5$ ，因此（7） $L_5=\varnothing$ ，转算法（9）步。

算法（9）输出 $L=L_2\cup L_3\cup L_4=\{\{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\}, \{b, e\}, \{c, d\}, \{c, e\}\}\cup\{\{a, b, c\},\{a, b, d\}, \{a, c, d\}, \{b, c, d\}, \{b, c, e\}\}\cup\{\{a, b, c, d\}\}$

例 8-4 对于频繁项集构成的集合 $L=C_2\cup C_3\cup C_4=\{\{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\}, \{b, e\}, \{c, d\}, \{c, e\}\}\cup\{\{a, b, c\},\{a, b, d\}, \{a, c, d\}, \{b, c, d\}, \{b, c, e\}\}\cup\{\{a, b, c, d\}\}$ 请求出它的最大频繁项集的集合。

解：因为最大频繁项集一定不是其它任何频繁项集的子集。因此，可以采用枚举法来寻找 $L$ 中的最大频繁项集，一般从项最多的频繁项集开始，检查它是否包含在某个频繁项集之中。
（1）因为 $L$ 中只有一个频繁4-项集 ${a, b, c, d\}$ ，故它不可能是 $L$ 中其它2-项集，3-项集的子集，所以它是一个最大频繁项集。
（2）对于 ${b, c, e\}$ ，因为它不是 ${a, b, c, d\}$ 的子集，也不是 $L$ 中其它3-项集的子集，更不是其它2-项集的子集，所以是最大频繁项集。
（3）因为 ${a, b, c\},\{a, b, d\},\{a, c, d\}$ 和 ${b, c, d\}$ 都是 ${a, b, c, d\}$ 的子集， ${a, b\},\{a, c\},\{a, d\},\{b, c\},\{b, d\}$ 和 ${c, d\}$ 都是 ${a, b, c, d\}$ 的子集, ${b, e\}$ 和 ${c, e\}$ 都是 ${b, c, e\}$ 的子集，所以它们都不是最大频繁项集。
故 $L$ 中有2个最大频繁项集，构成 $L_{max}=\{\{b, c, e\}，\{a, b, c, d\}\}$ 。

（二）产生关联规则

设 $X$ 为一个项集， $\varnothing≠Y\subset X$ ，则 $Y\Rightarrow(X-Y)$ 称为由 $X$ 导出的关联规则。
若 $X$ 是频繁项集，则它导出的关联规则必满足最小支持度要求，即 $(Y\Rightarrow(X-Y)) = Support (X)≥MinS\tag{8-4}$ 因此，只需检查 $Confidence(Y\Rightarrow(X-Y))$ 是否满足最小置信度 $M in C$ ，即可判断这个规则是否为强关联规则。

因为频繁项集X的任一子集 $Y$ 和 $X - Y$ 都是频繁项集，且 $S u pp or t (Y)$ 和 $S u pp or t (X - Y)$ 的值在发现频繁项集的时候已经计算出来。因此有 $Confidence(Y\Rightarrow(X-Y))=Support (X)/ Support (Y)\tag{8-5}$ 当 $Confidence(Y\Rightarrow(X-Y))≥MinC$ ，可知 $Y\Rightarrow(X-Y)$ 为强关联规则。

因此，我们可以得到关联规则的生成算法：

算法8-2 Apriori算法之强关联规则生成法
输入：所有频繁项集构成的集合 $L$ ，最小置信度 $M in C$
输出：所有强关联规则构成的集合 $S A R$
（1） $SAR=\varnothing$
（2）REPEAT
（3）取 $L$ 中一个未处理元素 $X$ (频繁项集)
（4）令 $Subsets(X)=\{Y|\varnothing≠Y\subset X\}$
（5）REPEAT
① 取 $S u b se t s (X)$ 的每一个未处理元素 $Y$ ，计算 $Confidence(Y\Rightarrow(X-Y))$
② 如果 $Confidence(Y\Rightarrow(X-Y))≥MinC$ ， $SAR=SAR\cup(Y\Rightarrow(X-Y))$
（6）UNTIL $S u b se t s (X)$ 中每个元素都已经处理
（7）UNTIL 集合 $L$ 中每个元素都已经处理
（8）输出 $S A R$

例 8-5 设最小置信度 $M in C = 0.6$ ，对于例8-4所得到的频繁项集的集合 $L=\{\{a, b\}，\{a, c\}，\{a, d\}，\{b, c\}，\{b, d\}，\{b, e\}，\{c, d\}，\{c, e\}\} \cup\{\{a, b, c\}，\{a, b, d\}，\{a, c, d\}，\{b, c, d\}，\{b, c, e\}\}\cup\{\{a, b, c, d\}\}$ 试求出所有的强关联规则。

解：从 $L$ 中取出第1个2-频繁项集 ${a, b\}$ ，它的两个非空真子集 ${a\}$ 和 ${b\}$ 可以生成 $\{a\}\Rightarrow\{b\}$ 和 $\{b\}\Rightarrow\{a\}$ 两个关联规则。 $Confidence(\{a\}\Rightarrow\{b\})=Support(\{a, b\})/ Support(\{a\})=3/3=1$ $Confidence(\{b\}\Rightarrow\{a\})=Support(\{a, b\})/Support(\{b\})=3/5=0.6$ 因此， $\{a\}\Rightarrow\{b\}$ 和 $\{b\}\Rightarrow\{a\}$ 都是强关联规则。

同理，求出 ${a, c\}，\{a, d\}，\{b, c\}，\{b, d\}，\{b, e\}，\{c, d\}，\{c, e\}$ 等7个2-频繁项集的关联规则，并判断是否强关联规则。对频繁3-项集 ${b, c, e\}$ 有6个非自身的非空真子集 ${b\},\{c\},\{e\},\{b,c\},\{b,e\}, \{c,e\}$ ，故共可生成6个关联规则，其置信度计算结果详见表8-7。

在这里插入图片描述
同理，可以计算求出其它频繁3-频繁集的强关联规则，也可以计算由 ${a, b, c, d\}$ 可以导出 $\{a\}\Rightarrow\{b,c,d\}$ ， $\{a,b\}\Rightarrow\{c, d\}$ 等14个关联规则，并找出相应的强关联规则。

穷举法可以通过枚举频繁项集生成所有的关联规则，并通过计算关联规则的置信度来判断该规则是否为强关联规则，但当一个频繁项集包含的项很多时，就会生成大量的候选关联规则，因为一个频繁项目集X能够生成 $2^{|X|}-2$ 个候选关联规则。

定理 8-3（关联规则性质1）：设 $X$ 为频繁项集， $\phi≠Y\subset X$ 且 $\phi≠Y'\subset Y$ 。若 $Y'\Rightarrow(X-Y')$ 为强关联规则，则 $Y\Rightarrow(X-Y)$ 也必是强关联规则。

比如，令 $X=\{b, c, e\}$ 且已知 $\{e\}\Rightarrow\{b,c\}$ 是强关联规则，则由定理8-3立即得出 $\{b,e\}\Rightarrow\{c\}$ 和 $\{c,e\}\Rightarrow\{b\}$ 都是强关联规则的结论，而不需计算这两个规则的置信度。

定理 8-4（关联规则性质2）：设 $X$ 为频繁项集， $\phi≠Y\subset X$ 且 $\phi≠Y'\subset Y$ 。若 $Y'\Rightarrow(X-Y')$ 不是强关联规则，则 $Y\Rightarrow(X-Y)$ 也不是强关联规则。

比如，令 $X=\{b, c, e\}$ 且已知 $\{b,c\}\Rightarrow\{e\}$ 不是强关联规则，则由定理8-4立即得出 $\{b\}\Rightarrow\{c,e\}$ 和 $\{c\}\Rightarrow\{b,e\}$ 都不是强关联规则的结论，也无需计算它们的置信度。

可以逐层生成关联规则，并利用以上性质2（定理8-4）进行剪枝，以减少关联规则生成的计算工作量。其基本思路是，首先产生后件只包含一个项的关联规则，然后两两合并这些关联规则的后件，生成后件包含两个项的候选关联规则，从这些候选关联规则中再找出强关联规则，以此类推。

比如，设 ${a,b,c,d\}$ 是频繁项集， $\{a,c,d\}\Rightarrow\{b\}$ 和 $\{b,c,d\}\Rightarrow\{a\}$ 是两个关联规则，则通过合并它们的后件生成候选规则的后件 ${a,b\}$ ，则候选规则的前件为 ${a,b,c,d\}-\{a,b\}=\{c,d\}$ ，由此即得候选规则 $\{c,d\}\Rightarrow\{a,b\}$ 。