---

在前文《强化学习的数学框架：马尔科夫决策过程 MDP》中，我们用马尔可夫过程抽象表示强化学习模型，并基于价值函数的贝尔曼方程迭代求出示例中的最优价值函数（策略），这种基于值迭代的方法，可以视为是动态规划的特例。本文基于前文的马尔可夫假设和贝尔曼方程，讨论如何使用动态规划（Dynamic Programming，DP）迭代地更新价值函数以求解强化学习¹。

1. 动态规划与强化学习的联系

动态规划是常见的用来解决优化问题的方法，但使用该方法求解的问题需要满足以下两个关键条件：

1. 具有最优子结构：即待优化问题的最优解可以由若干个小问题的最优解构成，在每个阶段求解子问题的最优解可以最终获得原问题的最优解；
2. 具有重叠子问题：即每个阶段计算的问题都与前面阶段的问题有所重叠，因此可以存储子问题的求解结果，基于前序子问题的结果递推出后续子问题的结果，来避免重复计算，加快计算效率。

这里可以用动态规划的方法实现前文案例中的两个计算，而这也是强化学习当中的两个基本问题：

1. 预测问题。给定强化学习的状态集 $S$，动作集 $A$，模型状态转化概率矩阵 $P$，采取动作的即时奖励 $R$，奖励衰减因子 $\gamma$，以及动作策略 $\pi$，在这些条件下，求解策略 $\pi$ 的状态价值函数 $v(\pi )$，该过程也称为 策略评估（Policy Evaluation）；
2. 控制问题。给定强化学习的状态集 $S$，动作集 $A$，模型状态转化概率矩阵 $P$，采取动作的即时奖励 $R$，奖励衰减因子 $\gamma$，求解最优的状态价值函数 $v_{\ast }$ 和最优策略 ${\pi }_{\ast }$，该过程也称为 策略迭代（Policy Iteration）。

在《强化学习的数学框架：马尔科夫决策过程 MDP》中我们用的是求解方程组的方式获得给定策略下的状态价值，以及最优价值函数，本文我们利用动态规划的方式，迭代地更新状态价值以及最优价值函数。由于状态价值和动作价值都能作为策略依据，这里我们以状态价值的贝尔曼方程为例：

$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })))$$

在给定策略下，我们假设在第 $k$ 轮迭代已经计算出了所有的状态的状态价值，那么在第 $k+1$ 轮我们可以利用第 $k$ 轮计算出的状态价值计算出第 $k+1$ 轮的状态价值，这样可以不断地逼近贝尔曼方程的实际值，将上述式子增加迭代周期下标，如下：

$$v_{(k+1)}(s)=\sum _{a\in A}\pi (a|s)(R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{(k)}(s^{\prime })))$$

可以通过赋予初始状态估计价值，然后代入上式不断迭代，得到更新后的新的状态估计价值，经过若干代之后得到的即为该策略下的状态价值函数 $v(\pi )$。

这里我们仍然沿用前文的案例，方便大家对两种求解方式有一个更深刻的理解，后续对大规模算例下DP求解和规划器求解的效率差异进行对比。

2. 利用动态规划求解最优价值函数

2.1 案例背景

现有一个关于学生开始的马尔科夫决策过程²，左上角的圆圈是当前的起始位置（状态），右上角的方框是终点位置（状态）。学生可以采取的动作为下图弧线上的红色字符串，有 $Study,Facebook,Quit,Sleep,Pub$，各个状态下采取动作对应的即时奖励 $R$ 的值在相关弧线上。现需要找到最优的状态价值或动作价值函数，以期能够达成最优策略。

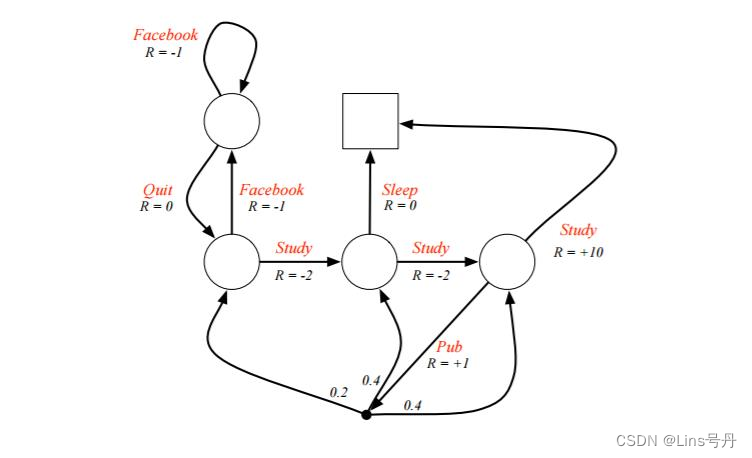
其中，在每个非结束状态处，都有两种可选择的动作，假设该例子中给定的策略 $\pi$ 是随机策略，在每个非结束状态都有 $\pi (a|s)=0.5$ 的概率选择其中一个动作，且定义奖励衰减因子 $\gamma =1$，即初始策略下会考虑当前及未来全量的累积奖励。

设置终点状态的价值为 $0$，其他各个非结束状态的初始估计值设为 $0$。定义左上 $s_1$、左下 $s_2$、中下 $s_3$、右下 $s_4$ 四个圆圈的状态价值为 $v_1,v_2,v_3,v_4$。

2.2 策略评估（预测）

利用动态规划求解给定策略下的状态价值函数，这个是强化学习的预测问题，通常称为策略评估（Policy Evaluation）。该方法下的基本思路是，从任意一个初始状态价值函数开始，依据给定的策略，结合贝尔曼方程、状态转移概率和动作的即时奖励，同步地迭代更新状态价值函数，直至其收敛（状态估计价值的迭代更新量非常少），即为该策略下最终的状态价值函数。

通过以下公式迭代地更新各个状态的估计价值：

$$v_{(k+1)}(s)=\sum _{a\in A}\pi (a|s)(R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{(k)}(s^{\prime })))$$

例如，初始时 $v1=0,v2=0,v3=0,v4=0$，将该值代入上式，得到第 $1$ 代的状态价值 $v_1^1=0.5\times (-1+0)+0.5\times (0+0)=-0.5$，依次类推，迭代 $10$ 次的代码及迭代后的结果如下：

v1,v2,v3,v4,v5 = 0,0,0,0,0
print(f"k={0} v1={v1}, v2={v2}, v3={v3}, v4={v4}")
for k in range(1, 10):new_v1 = 0.5*(-1+v1) + 0.5 * (v2)new_v2 = 0.5*(-1+v1) + 0.5 * (-2+v3)new_v3 = 0.5 * (-2+v4)new_v4 = 0.5*10 + 0.5 * (1+0.2*v2+0.4*v3+0.4*v4)v1,v2,v3,v4 = new_v1,new_v2,new_v3,new_v4print(f"k={k} v1={v1}, v2={v2}, v3={v3}, v4={v4}")

k=0 v1=0, v2=0, v3=0, v4=0
k=1 v1=-0.5, v2=-1.5, v3=-1.0, v4=5.5
k=2 v1=-1.5, v2=-2.25, v3=1.75, v4=6.25
k=3 v1=-2.375, v2=-1.375, v3=2.125, v4=6.875
k=4 v1=-2.375, v2=-1.625, v3=2.4375, v4=7.1625
k=5 v1=-2.5, v2=-1.46875, v3=2.58125, v4=7.2575
k=6 v1=-2.484375, v2=-1.459375, v3=2.62875, v4=7.320875
k=7 v1=-2.471875, v2=-1.4278125, v3=2.6604375, v4=7.3439875
k=8 v1=-2.44984375, v2=-1.40571875, v3=2.67199375, v4=7.35810375
k=9 v1=-2.42778125, v2=-1.388925, v3=2.679051875, v4=7.365447625

最终的结果收敛至给定策略下的状态价值函数，即得到了所有状态的基于随机策略的估计价值。

如上式所示，如果策略评估基于的是非常复杂的模型（状态空间、动作空间庞大）的话，动态规划的计算量仍非常庞大，每次迭代都对所有的状态价值进行更新的方法称为 同步动态规划算法，相比于 异步动态规划算法，同步更新的方法可能会导致更多的计算消耗，但相对更容易实现，以及在一些情况下更容易证明其收敛性。而异步更新的方式更适合于大规模状态空间的问题，即每次迭代有选择地更新部分状态，能极大提高算法效率，但由于更新的不确定性，其收敛性难以保证。

2.3 策略迭代（控制）

同理，我们利用动态规划的方法求解最优价值函数，这个是强化学习的控制问题，通常称为策略迭代（Policy Iteration）。类似于策略评估，该价值迭代能够从任意的初始状态价值函数迭代收敛至最优价值函数。

假设最优策略为 ${\pi }_{\ast }$，最优价值函数为 $v_{\ast }$，基于贪婪策略，智能体在某个状态下选择的行为是能，使其能够达到后续可能的状态中估计价值最大的。具体通过以下公式迭代地更新各个状态的最优估计价值，每经过一次迭代，状态的估计价值更倾向于选择的最优策略对应的后续状态：

$$v_{\ast }^{k+1}(s)=\underset{a}{\max }(R_t^a+\gamma \sum _{s^{\prime }\in S}(P_{s{s}^{\prime }}^a{v}_{\ast }^k(s^{\prime })))$$

更多时候，由于模型及其复杂，需要先对当前策略进行评估，得到当前策略的最终状态价值，再根据该状态价值以一定的方法（比如贪婪法）更新策略 ${\pi }_{\ast }$，循环该过程直至收敛到最优价值函数（策略）。

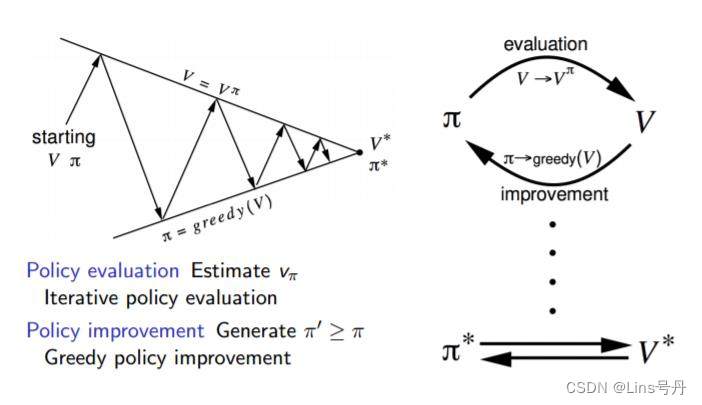
如上面的策略评估结果，在 $k=3$ 时，根据得到的状态价值就能得到最优的动作策略，因此在这里并不需要继续迭代至收敛，而是可以开始迭代地更新策略，这样能使得问题求解的收敛速度更快。

这里演示策略的迭代过程，例如，初始的状态价值为 $v1=0,v2=0,v3=0,v4=0$，将该值代入上式，更新得到第 $1$ 代的状态估计价值，依次类推，迭代 $10$ 次的代码及迭代的结果如下：

v1,v2,v3,v4,v5 = 0,0,0,0,0
print(f"k={0} v1={v1}, v2={v2}, v3={v3}, v4={v4}")
for K in range(1, 10):v1 = max(0+v2, -1+v1)v2 = max(-1+v1, -2+v3)v3 = max(0, -2+v4)v4 = max(10, 1+0.2*v2+0.4*v3+0.4*v4)print(f"K={K} v1={v1}, v2={v2}, v3={v3}, v4={v4}")

k=0 v1=0, v2=0, v3=0, v4=0
K=1 v1=0, v2=-1, v3=0, v4=10
K=2 v1=-1, v2=-2, v3=8, v4=10
K=3 v1=-2, v2=6, v3=8, v4=10
K=4 v1=6, v2=6, v3=8, v4=10
K=5 v1=6, v2=6, v3=8, v4=10
K=6 v1=6, v2=6, v3=8, v4=10
K=7 v1=6, v2=6, v3=8, v4=10
K=8 v1=6, v2=6, v3=8, v4=10
K=9 v1=6, v2=6, v3=8, v4=10

由于该案例较为简单，在迭代到第 $4$ 代时，价值函数已经收敛到最优。

总的而言，动态规划在求解规模较小的强化学习问题时易实现且有效，但当问题规模增大时，例如每个状态后续的可能状态非常多时，每次迭代都要对这些状态及之后的状态价值进行更新，总的计算量将指数级增长，因此，针对这个问题有学者提出蒙特卡洛方法来求解强化学习，该方法将在后续文章中进行介绍。

---

1. 强化学习（三）用动态规划（DP）求解：https://www.cnblogs.com/pinard/p/9463815.html ↩︎

2. UCL 强化学习第二章节讲义 https://www.davidsilver.uk/wp-content/uploads/2020/03/MDP.pdf ↩︎