【数学】主成分分析（PCA）的应用案例（Python）-编程知识

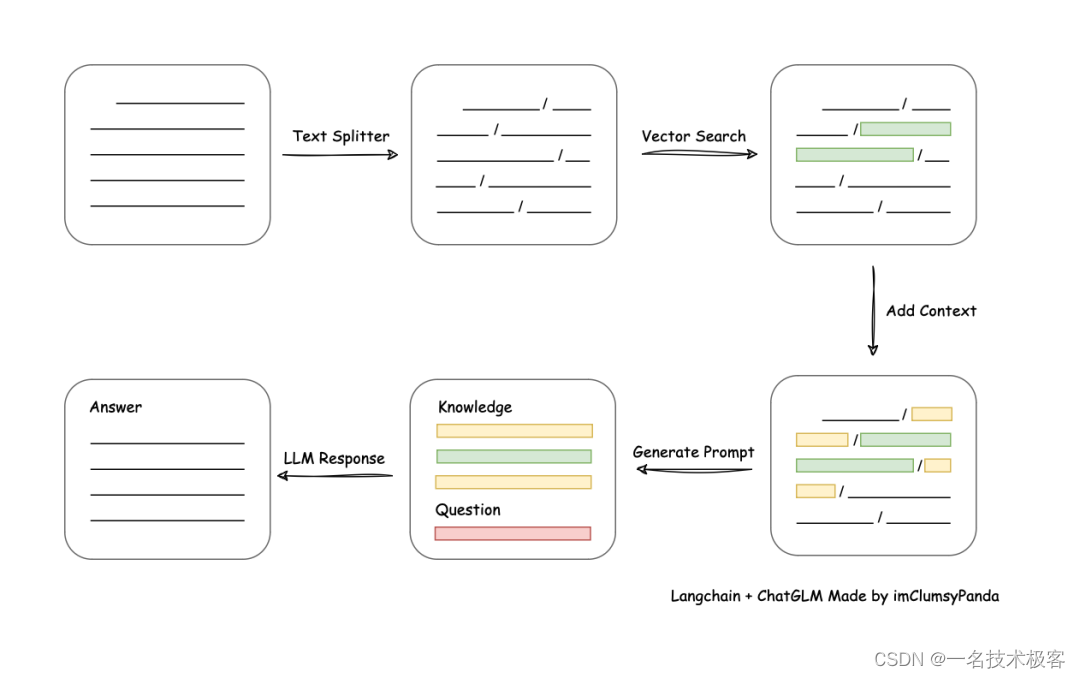
接着上篇PCA推导过程文章，本文结合图像来展示PCA的应用过程
Jupyter notebook 源文件在这里

1 借助库函数来PCA重建

使用sklearn库函数

# Import needed libs
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.metrics import mean_squared_error

导入图像数据，并输出数据大小

# Load the digits dataset
digits = load_digits()
X = digits.data
y = digits.target# Original data size
original_size = X.nbytes / (1024 * 1024)  # in megabytes
print("original data size is: %.2f MB" % original_size)

 original data size is: 0.88 MB

输出前十个数据图像

# Plot the first 10 samples as images
fig, axes = plt.subplots(1, 10, figsize=(12, 4))
for i in range(10):axes[i].imshow(X[i].reshape(8, 8), cmap='gray')axes[i].set_title(f"Label: {y[i]}")axes[i].axis('off')
plt.tight_layout()
plt.show()

在这里插入图片描述

打印第一个数据的矩阵形式

# Print the first 1 sample in matrix form
for i in range(1):print(f"Sample {i+1}:")sample_matrix = X[i].reshape(8, 8)  # Reshape the row vector to a matrixprint(sample_matrix)print(f"Label: {y[i]}")print()

    Sample 1:[[ 0.  0.  5. 13.  9.  1.  0.  0.][ 0.  0. 13. 15. 10. 15.  5.  0.][ 0.  3. 15.  2.  0. 11.  8.  0.][ 0.  4. 12.  0.  0.  8.  8.  0.][ 0.  5.  8.  0.  0.  9.  8.  0.][ 0.  4. 11.  0.  1. 12.  7.  0.][ 0.  2. 14.  5. 10. 12.  0.  0.][ 0.  0.  6. 13. 10.  0.  0.  0.]]Label: 0

写一些用来辅助衡量重建效果的函数，一会用到

# Function to calculate reconstruction error
def reconstruction_error(original, reconstructed):return mean_squared_error(original, reconstructed)# Function to perform PCA and reconstruct data with n_components
def perform_pca(n_components):pca = PCA(n_components=n_components)X_pca = pca.fit_transform(X)X_reconstructed = pca.inverse_transform(X_pca)return X_reconstructed, pca

根据输入的主成分个数来压缩数据的函数

# Function to perform PCA, and visualize result. Input is the number of principle components
def analyze_pca(n_components):X_reconstructed, pca = perform_pca(n_components)reconstruction_error_val = reconstruction_error(X, X_reconstructed)print(f"Number of Components: {n_components}, Reconstruction Error: {reconstruction_error_val}")# Size of compressed filecompressed_size = (pca.components_.nbytes + pca.mean_.nbytes + X_reconstructed.nbytes) / (1024 * 1024)  # in megabytesprint(f"Size of Compressed File: {compressed_size} MB")# Difference in sizesize_difference = original_size - compressed_sizeprint(f"Difference in Size: {size_difference} MB")# Plot original and reconstructed images for each digitfig, axes = plt.subplots(2, 10, figsize=(10, 2))for digit in range(10):digit_indices = np.where(y == digit)[0]  # Indices of samples with the current digitoriginal_matrix = X[digit_indices[0]].reshape(8, 8)  # Take the first sample for each digitreconstructed_matrix = np.round(X_reconstructed[digit_indices[0]].reshape(8, 8), 1)  # Round to one decimal placeaxes[0, digit].imshow(original_matrix, cmap='gray')axes[0, digit].axis('off')axes[1, digit].imshow(reconstructed_matrix, cmap='gray')axes[1, digit].axis('off')plt.suptitle(f'Reconstruction with {n_components} Components')plt.show()# Print the first data's matrixprint("Original Matrix of the First Data:")print(original_matrix)# Print the reconstruction matrixprint("\nReconstruction Matrix of the First Data:")print(reconstructed_matrix)

结果展示：使用一个主成分来压缩图像并对比结果

analyze_pca(1)

    Number of Components: 1, Reconstruction Error: 15.977678462244262Size of Compressed File: 0.87841796875 MBDifference in Size: -0.0009765625 MB

在这里插入图片描述

Original Matrix of the First Data:[[ 0.  0. 11. 12.  0.  0.  0.  0.][ 0.  2. 16. 16. 16. 13.  0.  0.][ 0.  3. 16. 12. 10. 14.  0.  0.][ 0.  1. 16.  1. 12. 15.  0.  0.][ 0.  0. 13. 16.  9. 15.  2.  0.][ 0.  0.  0.  3.  0.  9. 11.  0.][ 0.  0.  0.  0.  9. 15.  4.  0.][ 0.  0.  9. 12. 13.  3.  0.  0.]]Reconstruction Matrix of the First Data:[[ 0.   0.4  6.4 12.6 12.   6.3  1.4  0.1][ 0.   2.6 11.7 11.2 10.5  9.4  1.9  0.1][ 0.   3.   9.4  5.8  8.   8.7  1.6  0. ][ 0.   2.1  7.7  9.  11.1  7.8  2.   0. ][ 0.   1.5  5.6  8.2  9.8  8.5  2.8  0. ][ 0.   1.   5.2  5.9  6.5  8.2  3.7  0. ][ 0.   0.8  7.8  9.   8.8  9.5  4.1  0.2][ 0.   0.4  6.8 12.9 11.9  7.3  2.3  0.4]]

再选择5个主成分来压缩图像，比较重建效果。

analyze_pca(5)

    Number of Components: 5, Reconstruction Error: 8.542447616771714Size of Compressed File: 0.88037109375 MBDifference in Size: -0.0029296875 MB

Original Matrix of the First Data:[[ 0.  0. 11. 12.  0.  0.  0.  0.][ 0.  2. 16. 16. 16. 13.  0.  0.][ 0.  3. 16. 12. 10. 14.  0.  0.][ 0.  1. 16.  1. 12. 15.  0.  0.][ 0.  0. 13. 16.  9. 15.  2.  0.][ 0.  0.  0.  3.  0.  9. 11.  0.][ 0.  0.  0.  0.  9. 15.  4.  0.][ 0.  0.  9. 12. 13.  3.  0.  0.]]Reconstruction Matrix of the First Data:[[-0.   0.2  5.2 11.1 12.1  7.   1.6  0.1][ 0.   2.1 11.2 10.7  9.7  9.6  2.3  0.2][ 0.   3.1 11.2  6.2  6.   9.2  2.5  0.1][ 0.   3.1 10.3  9.   9.6  9.6  2.9  0. ][ 0.   2.2  6.   5.3  8.  11.6  3.9  0. ][ 0.   1.2  4.2  1.9  4.9 11.7  5.1  0. ][ 0.   0.6  6.7  6.2  8.8 12.1  4.4  0.2][ 0.   0.2  5.4 12.1 13.4  8.2  1.8  0.3]]

2 手动计算PCA解码矩阵

按照PCA的原理公式，来分布计算PCA的解码矩阵，便于理解其流程。

输入原图并查看

# Then use step-by-step wat to calculate the PCA steps;
# Take the first data point for analysis
first_data = X[0]
print("Raw input data: \n", X[0])
print("Raw data shape: ", X[0].shape)
# Reshape the data point into a 2D array (image)
input_matrix = first_data.reshape(8, 8)print("Input matrix: ")
for row in input_matrix:print(" ".join(f"{val:4.0f}" for val in row))# Print the original matrix (image)
plt.imshow(input_matrix, cmap='gray')
plt.title("Input matrix (Image)")
plt.axis('off')
plt.show()

    Raw input data: [ 0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.  3.15.  2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.  0.0.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10. 12.0.  0.  0.  0.  6. 13. 10.  0.  0.  0.]Raw data shape:  (64,)Input matrix: 0    0    5   13    9    1    0    00    0   13   15   10   15    5    00    3   15    2    0   11    8    00    4   12    0    0    8    8    00    5    8    0    0    9    8    00    4   11    0    1   12    7    00    2   14    5   10   12    0    00    0    6   13   10    0    0    0

在这里插入图片描述

根据公式计算 $X^TX$ ，或输入数据的协方差矩阵Cov：

# Transpose X
X_transpose = input_matrix.T# Calculate X^T * X
XTX = np.multiply(X_transpose, input_matrix)
# Or use cov to cal:
# XTX = np.cov(X_transpose)# Print the result
print("Matrix of XTX:")
print(XTX)# Step 1: Calculate the covariance matrix
covariance_matrix = np.cov(X_transpose)print(covariance_matrix.shape)

    Matrix of XTX:[[  0.   0.   0.   0.   0.   0.   0.   0.][  0.   0.  39.  60.  50.  60.  10.   0.][  0.  39. 225.  24.   0. 121. 112.   0.][  0.  60.  24.   0.   0.   0.  40.   0.][  0.  50.   0.   0.   0.   9.  80.   0.][  0.  60. 121.   0.   9. 144.  84.   0.][  0.  10. 112.  40.  80.  84.   0.   0.][  0.   0.   0.   0.   0.   0.   0.   0.]](8, 8)

矩阵特征分解，打印出矩阵的特征值和特征向量：

# Step 2: Calculate the eigenvalues and eigenvectors of the covariance matrix
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)# Print the eigenvalues
print("\nStep 2: Eigenvalues")
print(eigenvalues)# Print the eigenvectors
print("\nStep 2: Eigenvectors")
print(eigenvectors)

 Step 2: Eigenvalues[8.92158455e+01 3.14545089e+01 7.61850164e+00 2.85144338e+002.01453633e-01 1.53898738e-02 0.00000000e+00 0.00000000e+00]Step 2: Eigenvectors[[ 0.          0.          0.          0.          0.          0.1.          0.        ][-0.20365153  0.09344175  0.07506402 -0.23052329 -0.41043409 -0.850037030.          0.        ][-0.22550077 -0.48188982  0.20855091  0.79993174 -0.1168451  -0.141048050.          0.        ][ 0.65318552 -0.28875672 -0.59464342  0.12374602  0.11324705 -0.328982470.          0.        ][ 0.48997693 -0.31860576  0.39448425 -0.20610464 -0.63307453  0.243993180.          0.        ][-0.33563583 -0.75773097 -0.0607778  -0.49775699  0.24837474  0.006811390.          0.        ][-0.35818338 -0.00212894 -0.66178497  0.03760326 -0.58531429  0.299556280.          0.        ][ 0.          0.          0.          0.          0.          0.0.          1.        ]]

使用一个主成分的情况下，选择最大的特征值所对应的特征向量构成解码矩阵：


# Find the index of the largest eigenvalue
largest_eigenvalue_index = np.argmax(eigenvalues)# Step 3: Use the eigenvector corresponding to the largest eigenvalue to form the decoding matrix
decoding_matrix = eigenvectors[:, largest_eigenvalue_index].reshape(-1, 1)# Print the decoding matrix
print("\nStep 3: Decoding Matrix")
print(decoding_matrix)```bashStep 3: Decoding Matrix[[ 0.        ][-0.20365153][-0.22550077][ 0.65318552][ 0.48997693][-0.33563583][-0.35818338][ 0.        ]]

查看重建效果：


# Step 4: Reconstruct the data point using the decoding matrix
reconstructed_data = np.dot(decoding_matrix, decoding_matrix.T.dot(input_matrix))# Reshape the reconstructed data into a 2D array (image)
reconstructed_matrix = reconstructed_data.reshape(8, 8)# Print the reconstructed matrix
print("\nStep 4: Reconstructed Matrix")
print(reconstructed_matrix)

Step 4: Reconstructed Matrix[[ 0.          0.          0.          0.          0.          0.0.          0.        ][ 0.         -0.47394076  0.6065763   1.07867928  1.21253812  0.86059781-0.80922666  0.        ][ 0.         -0.52478863  0.67165429  1.19440797  1.34262817  0.95292911-0.89604648  0.        ][ 0.          1.52010272 -1.9455138  -3.45972209 -3.88905673 -2.760254442.59548821  0.        ][ 0.          1.14028135 -1.45939683 -2.59525656 -2.91731524 -2.070561811.946965    0.        ][ 0.         -0.78109652  0.99969169  1.77775938  1.99837065  1.41834173-1.3336775   0.        ][ 0.         -0.83356951  1.0668496   1.89718681  2.13261844  1.51362398-1.42327212  0.        ][ 0.          0.          0.          0.          0.          0.0.          0.        ]]


# Plot the reconstructed matrix (image)
plt.imshow(reconstructed_matrix, cmap='gray')
plt.title("Reconstructed Matrix (Image)")
plt.axis('off')
plt.show()