【静态分析】软件分析课程实验A1-活跃变量分析和迭代求解器-编程知识

1 作业导览

为 Java 实现一个活跃变量分析（Live Variable Analysis）。
实现一个通用的迭代求解器（Iterative Solver），用于求解数据流分析问题，也就是本次作业中的活跃变量分析。

Live Variable Analysis 详见【静态分析】静态分析笔记03 - 数据流分析（应用）-CSDN博客。

我们已经在 Tai-e 的框架代码中提供了你需要的一切基础设施，包括但不限于：程序分析接口、常用数据结构（如数据流信息的表示）、必要的程序信息（如控制流图）等内容。由此，你就可以便利地在 Tai-e 上实现各类数据流分析了。例如在本次作业中，你要在框架代码中补全一些关键部分，从而实现要求的活跃变量分析与迭代求解器。

需要特别注意的是，所有作业文档都只会简要地介绍本次作业中必要的一些 API。因此，如果要搞清楚 API 的实现机制、真正理解框架代码，你必须留出时间阅读、理解相关类的源代码和相应的注释。这是你提升快速上手复杂代码能力的必经之路。

2 实现活跃变量分析

2.1 Tai-e 中你需要了解的类

为了在 Tai-e 中实现活跃变量分析，你需要了解的类有：

pascal.taie.analysis.dataflow.analysis.DataflowAnalysis

这是一个抽象的数据流分析类，是具体的数据流分析与求解器之间的接口。也就是说，一个具体的数据流分析（如活跃变量分析）需要实现它的接口，而求解器（如迭代求解器）需要通过它的接口来求解数据流。

需要注意的是，这里的API与课程中介绍的稍有区别：为了简单起见，这里的transfer函数处理的是单条语句而非程序块。
pascal.taie.ir.exp.Exp

这是 Tai-e 的 IR 中的一个关键接口，用于表示程序中的所有表达式。它含有很多子类，对应各类具体的表达式。下面是一个 Exp 类继承结构的简单图示：

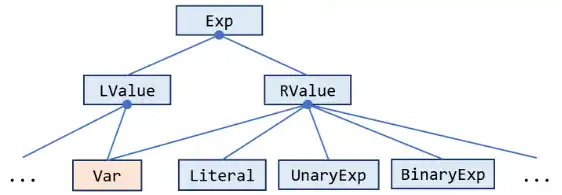
在 Tai-e 的 IR 中，我们把表达式分为两类：LValue 和 RValue。前者表示赋值语句左侧的表达式，如变量（x = … ）、字段访问（x.f = …）或数组访问（x[i] = …）；后者对应地表示赋值语句右侧的表达式，如数值字面量（… = 1;）或二元表达式（… = a + b;）。而有些表达式既可用于左值，也可用于右值，就比如变量（用Var类表示)。因为本次作业只进行活跃变量分析，所以你实际上只需要关注 Var 类就足够了。

pascal.taie.ir.stmt.Stmt

这是 Tai-e 的 IR 中的另一个关键接口，它用于表示程序中的所有语句。对于一个典型的程序设计语言来说，每个表达式都属于某条特定的语句。为了实现活跃变量分析，你需要获得某条语句中定义或使用的所有表达式中的变量。Stmt 类贴心地为这两种操作提供了对应的接口：

Optional<LValue> getDef()
List<RValue> getUses()

每条 Stmt 至多只可能定义一个变量、而可能使用零或多个变量，因此我们使用 Optional 和 List 包装了 getDef() 和 getUses() 的结果。

pascal.taie.analysis.dataflow.fact.SetFact<Var>

这个泛型类用于把 data fact 组织成一个集合。它提供了各种集合操作，如添加、删除元素，取交集、并集等。
pascal.taie.analysis.dataflow.analysis.LiveVariableAnalysis

这个类通过实现 DataflowAnalysis 的接口来定义具体的活跃变量分析。你需要按照第 2.2 节中的说明补全这个类。

需要注意：

本次作业的每个基本块仅含有一条指令
实验的结果最后存储在参数 DataflowResult<Node, Fact> result中
用到了Java的一些特性
- Optional特性：isPresent() 和 get()的使用
- 泛型特性

2.2 你的任务

你的第一个任务是实现 LiveVariableAnalysis 中的如下 API：

SetFact newBoundaryFact(CFG)
SetFact newInitialFact()
void meetInto(SetFact,SetFact)
boolean transferNode(Stmt,SetFact,SetFact)

此处 meetInto() 的设计可能与你设想的稍有差别：它接受 fact 和 target 两个参数并把 fact 集合并入 target 集合。这个函数有什么用呢？考虑一下上图中 meetInto() 附近的那行伪代码，它会取出 B 的所有后继，然后把它们 IN facts 的并集赋给 OUT[B]。如果这行代码用 meetInto() 来实现，那么我们就可以根据下图所示，用 meetInto(IN[S], OUT[B]) 把 B 的每个后继 S 的 IN fact 直接并入到 OUT[B] 中：

这种设计还有更多的优化空间：我们可以忽略一些不变的 IN fact 来提高效率。例如在某次迭代中，如果 IN[S2] 有改变而 IN[S3] 没有，我们就不必依照课堂上讲述的办法求出 IN[S2] 和 IN[S3] 的并，而大可以忽略 IN[S3]，只把 IN[S2] 并入 OUT[S1]。不过这个优化超出了本次作业的范畴，你不用考虑实现它。

当然，为了实现上面所说的 meet 策略，你需要在初始化阶段给每条语句的 OUT[S] 赋上和 IN[S] 一样的初值。

除了 meetInto() ，其他 API 的实现都直接依照了课上讲述的算法。需要注意的是，框架中LiveVariableAnalysis 的 API 都继承自 DataflowAnalysis，而该类为了支持各种数据流分析，接口中可能包含了一些你用不上的参数。因此，某些参数在作业中用不上是正常现象。

我们已经提供了四个 API 的框架代码，你的任务就是补全标有“TODO – finish me”的部分。

import pascal.taie.ir.exp.*;
import java.util.List;
import java.util.Optional;/*** Implementation of classic live variable analysis.*/
public class LiveVariableAnalysis extendsAbstractDataflowAnalysis<Stmt, SetFact<Var>> {/*** 负责创建和初始化虚拟结点的 Data Flow Fact** @return 初始化好的节点*/@Overridepublic SetFact<Var> newBoundaryFact(CFG<Stmt> cfg) {// TODO - finish mereturn new SetFact<>();}/*** 负责创建和初始化控制流图中除了 Entry 和 Exit 之外的结点的 Data Flow Fact* 控制流图中一个结点的 IN 和 OUT 分别对应一个 Data Flow Fact ，记录当前程序点时变量的状态** @return 初始化好的节点*/@Overridepublic SetFact<Var> newInitialFact() {// TODO - finish me// 节点初始化为空return new SetFact<>();}/*** 负责处理 transfer function 之前可能遇到多个 IN 时的合并处理*/@Overridepublic void meetInto(SetFact<Var> fact, SetFact<Var> target) {// TODO - finish metarget.union(fact);}/*** 负责实现控制流图中结点的 transfer function:* IN[B] = 本块中 use 出现在 define 之前的变量 U（OUT[B] 的 live 情况 - 本块中 define 的变量）。* 由于本次作业的每个基本块仅含有一条指令，所以可以不用考虑变量的 use 是否出现在 define 之前** @return 如果 IN 改变，返回 true；否则返回 false*/@Overridepublic boolean transferNode(Stmt stmt, SetFact<Var> in, SetFact<Var> out) {// TODO - finish meOptional<LValue> def = stmt.getDef();List<RValue> uses = stmt.getUses();SetFact<Var> newSetFact = new SetFact<>();newSetFact.union(out);if(def.isPresent()) {if(def.get() instanceof Var) {newSetFact.remove((Var) def.get());}}for (RValue use : uses) {if (use instanceof Var) {newSetFact.add((Var) use);}}if (!in.equals(newSetFact)) {in.set(newSetFact);return true;}return false;}
}

3 实现迭代求解器

3.1 Tai-e 中你需要了解的类

为了在 Tai-e 中实现迭代求解器，你需要了解的类有：

pascal.taie.analysis.dataflow.fact.DataflowResult

该类对象用于维护数据流分析的 CFG 中的 fact。你可以通过它的 API 获取、设置 CFG 节点的 IN facts 和 OUT facts。
pascal.taie.analysis.graph.cfg.CFG

这个类用于表示程序中方法的控制流图（control-flow graphs）。它是可迭代的，也就是说你可以通过一个 for 循环遍历其中的所有节点：

CFG<Node> cfg = ...;
for (Node node : cfg) {...
}

你可以通过 CFG.getPredsOf(Node) 和 CFG.getSuccsOf(Node) 这两个方法遍历 CFG 中节点的所有前驱和后继，比如你可以写：

for (Node succ : cfg.getSuccsOf(node)) {...
}

pascal.taie.analysis.dataflow.solver.Solver

这是数据流分析求解器的基类，包含了求解器的抽象功能。本次作业要实现的迭代求解器就是它的一个派生类（下次作业中的 worklist 求解器也是）。Tai-e 会构建待分析程序的 CFG 并传给 Solver.solve(CFG)，然后世界就开始运转了。你可能注意到了，这个类中有两组 initialize 和 doSolve 方法，分别用于处理前向和后向的数据流分析。虽然稍显冗余，但在这样的设计下代码结构会更干净、直接一些。这个类也是需要你补全实现的，这在第 3.2 节中进一步解释。
pascal.taie.analysis.dataflow.solver.IterativeSolver

这个类扩展了 Solver 的功能并实现了迭代求解算法。当然，它也有待你补全。

3.2 你的任务

你的第二个任务是实现上面提到的 Solver 类的两个方法：

Solver.initializeBackward(CFG,DataflowResult)
IterativeSolver.doSolveBackward(CFG,DataflowResult)

因为活跃变量分析是一个后向分析，所以你只需要关注后向分析相关的方法就足够了。在 initializeBackward() 中，你需要实现第 2.2 节中算法的前三行；在 doSolveBackward() 则要完成对应的 while 循环。

提示：

每个 Solver 对象都在字段 analysis 中保存了相应的数据流分析对象，在本次作业中就是一个 LiveVariableAnalysis 对象。你需要用它提供的相关接口来实现分析求解器。

/*** 实现算法前三行的初始化操作* 调用函数 newBoundaryFact 和 newInitialFact (DataflowAnalysis 中)*/protected void initializeBackward(CFG<Node> cfg, DataflowResult<Node, Fact> result) {// TODO - finish me// Init Exit noderesult.setInFact(cfg.getExit(), analysis.newBoundaryFact(cfg));// Init other nodesfor (Node node : cfg) {if (!cfg.isExit(node)) {result.setInFact(node, analysis.newInitialFact());result.setOutFact(node, analysis.newInitialFact());}}}

/*** 完成 while 循环*/@Overrideprotected void doSolveBackward(CFG<Node> cfg, DataflowResult<Node, Fact> result) {// TODO - finish meboolean flag = true;while (flag) {flag = false;for (Node node : cfg) {if (cfg.isExit(node)) continue;  // 出口节点不需要特殊处理// 获取当前节点的 OUT 和 INFact outFact = result.getOutFact(node);Fact inFact = result.getInFact(node);// 对于每个节点，调用函数 meetInto 和 transferNode (DataflowAnalysis 中)for (Node succs : cfg.getSuccsOf(node)) {Fact succsInFact = result.getInFact(succs);  // 获取 succs 节点的 IN 的 Fact 值analysis.meetInto(succsInFact, outFact);}if (analysis.transferNode(node, inFact, outFact)) {flag = true;}}}}

4 运行与测试

你可以按我们在 Tai-e 框架（教学版）配置指南中提到的方式来运行你的分析。

在本作业中，Tai-e 对输入类的每个方法进行活跃变量分析，并输出分析的结果，也就是每个语句的 OUT fact 所包含的数据流信息（活跃变量）：

--------------------<Assign: int assign(int,int,int)> (livevar)--------------------
[0@L4] d = a + b; null
[1@L5] b = d; null
[2@L6] c = a; null
[3@L7] return b; null

输出结果的每一行以该语句的位置信息开始，例如 [0@L4] 表示该语句在 IR 中的索引为 0，且在源码中处于第 4 行。输出结果的每一行末尾为该语句的 OUT fact，（当你未完成作业时结果为 null）。当你完成了所有的空缺代码后，分析的输出应当形如：

--------------------<Assign: int assign(int,int,int)> (livevar)--------------------
[0@L4] d = a + b; [a, d]
[1@L5] b = d; [a, b]
[2@L6] c = a; [b]
[3@L7] return b; []

注意：此处 return b; 这条语句也用到了 b 变量。

此外，Tai-e 将被分析方法的控制流图输出到 output/ 文件夹，它们被存储为 .dot 文件，你可以用可视化工具 Graphviz来查看这些控制流图。

我们为本次作业提供了测试驱动类 pascal.taie.analysis.dataflow.analysis.LiveVarTest，你可以按照 Tai-e 框架（教学版）配置指南中描述的方式来测试你的实现是否正确。