日升时奋斗,日落时自省
目录
1、二分法
2、二分法问题
2.1 、在排序数组中查找元素的第一个和最后一个位置
2.2、搜索插入位置
2.3、山脉数组的峰顶索引
2.4、0-n-1中缺失的数字
1、二分法
二分法是比较简单的一种查找算法,但是效率很高,很多友友们也会觉得二分法没有什么好说的,就是取中,对比,位置变化,其实大体上也就是这么三个
注:二分法适用条件 有二段性 ,其实就是有规律的分段,排序就是其中常见的一种
第一类普通二分法:

代码:
public static int search(int[] nums,int target){//二分范围就是 具有二段性的范围 这里是一个排序好的数组具有 二段性//left就是左边界 right 就是右边界int left = 0,right =nums.length-1;//判断条件 为什么会有等于//因为这里是为了可以找到 我们要的 并且存在的下标//等于的情况就是我们需要找的 while (left<=right){int mid = left + (right - left) /2;//如果目标值大于中间值 left给小了//target的存在位置一定大于mid left是当前区间最小位置 更新这里left的位置就是mid+1if(target>nums[mid]){left=mid+1;//如果目标值小于中间值 right给大了//target的存在位置一定小于mid right是当前区间最大位置 更新这里right的位置就是mid-1}else if(target<nums[mid]){right=mid-1;}else {return mid;}}return -1;}第二种就是找左边界值(二分法):
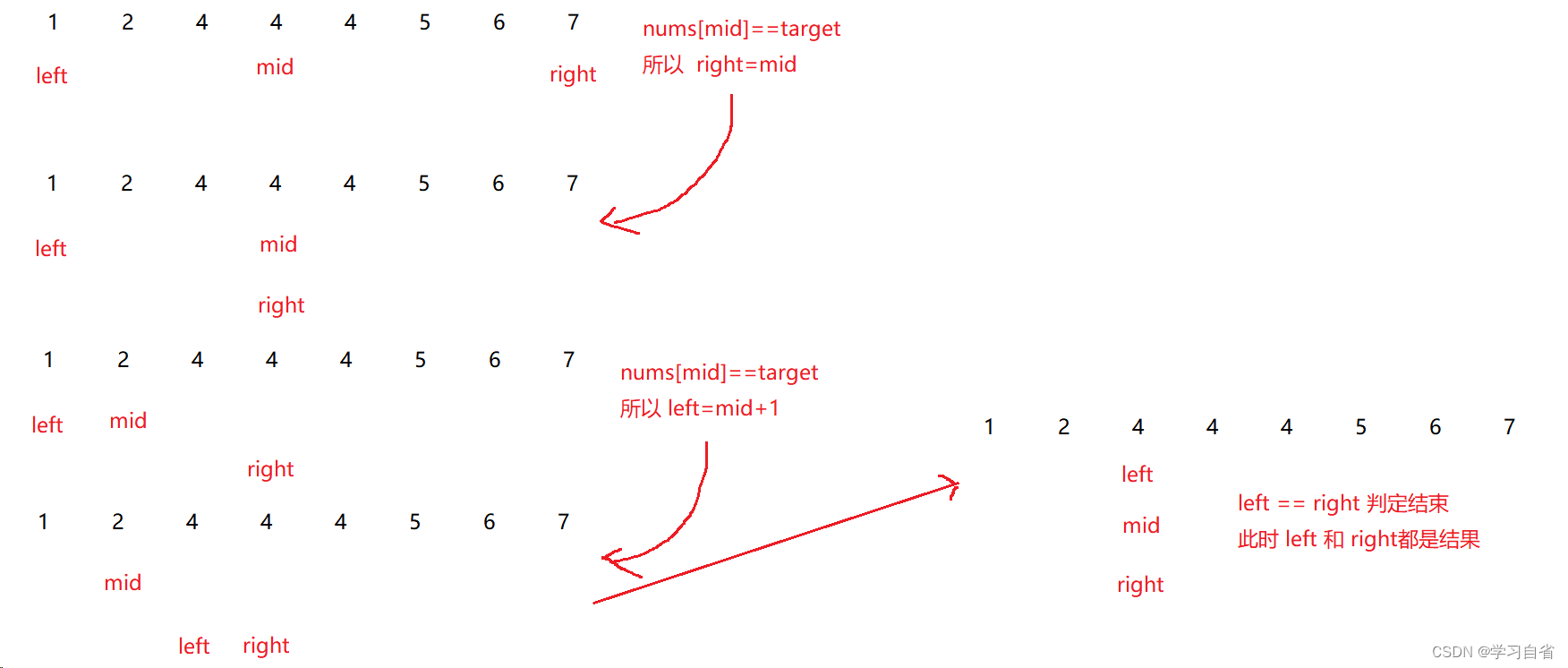
有没有见过1,2,3,4,4,4,4,5,7,8这种需要你找到当前元素中找到最左边4的位置
这就是特殊类型的二分法了
注:建议先看代码在看图
图示:
代码:
public static int search(int[] nums,int target){int left = 0, right = nums.length - 1;//不在是为了找到 对应的值 而是一个极端的下标 //所以没有等号while(left<right){//寻找左端点 (right-left)/2 是靠左的int mid = left + (right - left)/2;if(nums[mid]<target){//目标值大于 中间值 说明left偏小left=mid+1;}else {//right不同 如果target小等于 right边小到 mid 位置//为啥呢 因为 target==nums[mid] 那此时极端下标就是mid//right等于相等情况的下标 midright=mid;}}//left==right 此时 所以返回right也可以 return left;}第二种就是找右边界值(二分法):
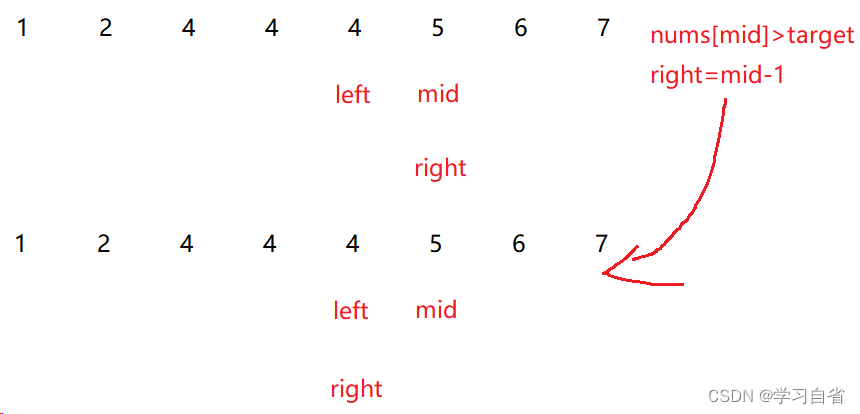
有没有见过1,2,3,4,4,4,4,5,7,8这种需要你找到当前元素中找到最右边4的位置
这就是特殊类型的二分法了
注:方法大体相同
mid = left + (right - left + 1)/2 表示取值靠右
剩下的就是条件了
图示:

代码:
public static int search(int[] nums,int target){int left = 0, right = nums.length - 1;//不在是为了找到 对应的值 而是一个极端的下标//所以没有等号while(left<right){//寻找左端点 (right-left+1)/2 是靠右的int mid = left + (right - left+1)/2;if(nums[mid]>target){//目标值小于 中间值 说明right偏大right=mid-1;}else {//right不同 如果target大等于 left边小 到mid 位置//为啥呢 因为 target==nums[mid] 那此时极端下标就是mid//left等于相等情况的下标 midleft=mid;}}//left==right 此时 所以返回right也可以return left;}2、二分法问题
2.1 、在排序数组中查找元素的第一个和最后一个位置
题目来源:. - 力扣(LeetCode)
其实就是把两种特殊二分进行使用 找左值 也 找右值
代码:
public int[] searchRange(int[] nums, int target) {//题目说了要两个 下标 咱们建立一个数组来放置int[] ret=new int[2];//例题已经给了 要求为空 数组返回 -1 -1if(nums.length==0){return new int[]{-1,-1};}//二分两边的位置 int left =0, right=nums.length-1;//寻找左端点while(left<right){//选择条件靠左int mid = left+(right-left)/2;if(nums[mid]<target){left=mid+1;}else if(nums[mid]>=target){right=mid;}}//此时进行一次判断 如果left没有找到也就是没有目标值if(nums[left]!=target){//不存在直接返回 -1 -1return new int[]{-1,-1};}//记录一下ret[0]=left;//其实这里 可以不用在初始化的 //为了方便友友们看懂left=0;right=nums.length-1;//寻找右端点while(left<right){//靠右条件int mid =left+(right-left+1)/2;if(nums[mid]>target){right=mid-1;}else if(nums[mid]<=target){left=mid;}}//记录右下标ret[1]=left;return ret;}注:不要害怕长,整个代码都是前面的代码构成的,算是套模板
2.2、搜索插入位置
题目来源:. - 力扣(LeetCode)
在一个数组中找目标元素,如果存在返回下标,如果不存在找到排序好的下标
代码:
public int searchInsert(int[] nums, int target) {int left=0,right=nums.length-1;while(left<right){//找右值int mid=left+ (right-left+1)/2;if(nums[mid]<=target){left=mid;}else{right=mid-1;}}//如果目标值大于left 说明没有找到 //此时left+1就是排序好的下标if(nums[left]<target){return left+1;}else {//相等就是找到了return left;}}2.3、山脉数组的峰顶索引
题目来源:. - 力扣(LeetCode)
图示:
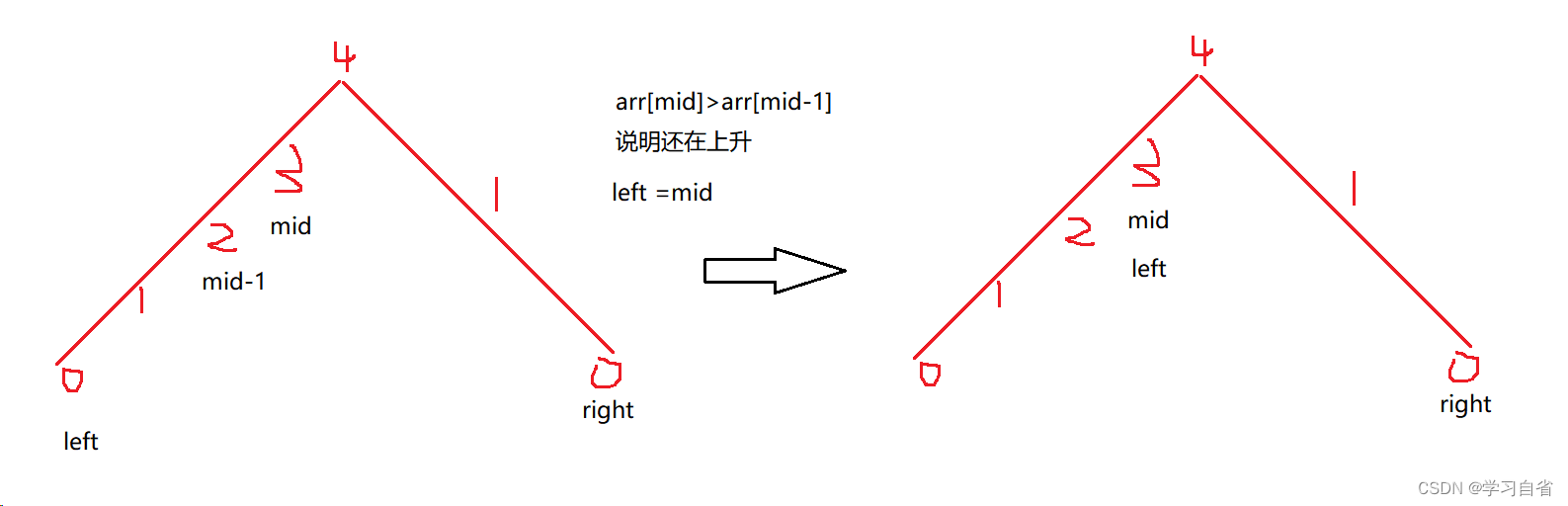
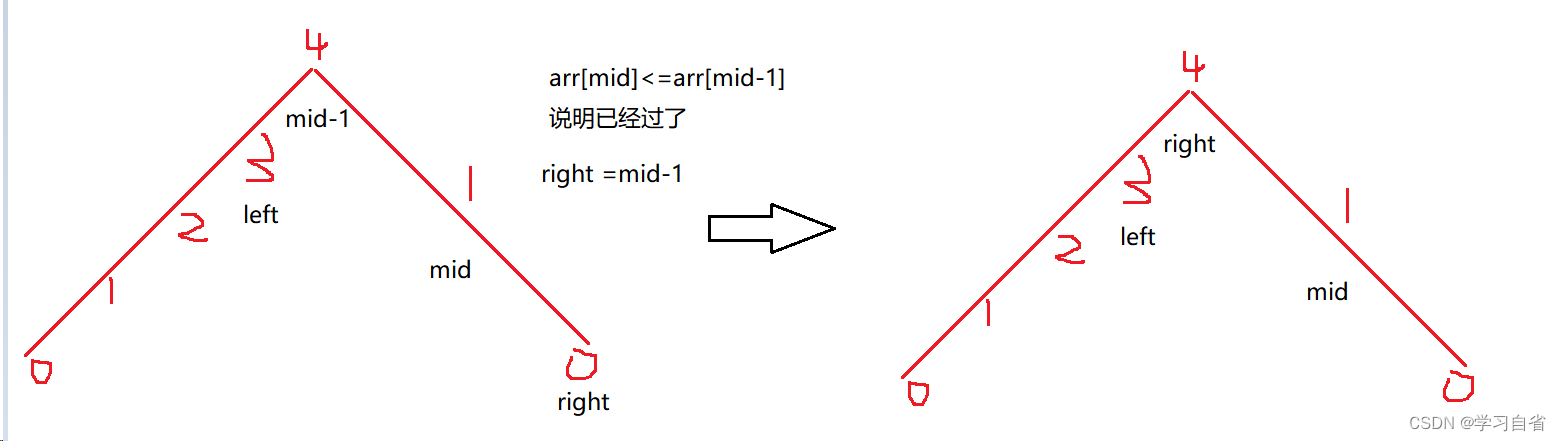
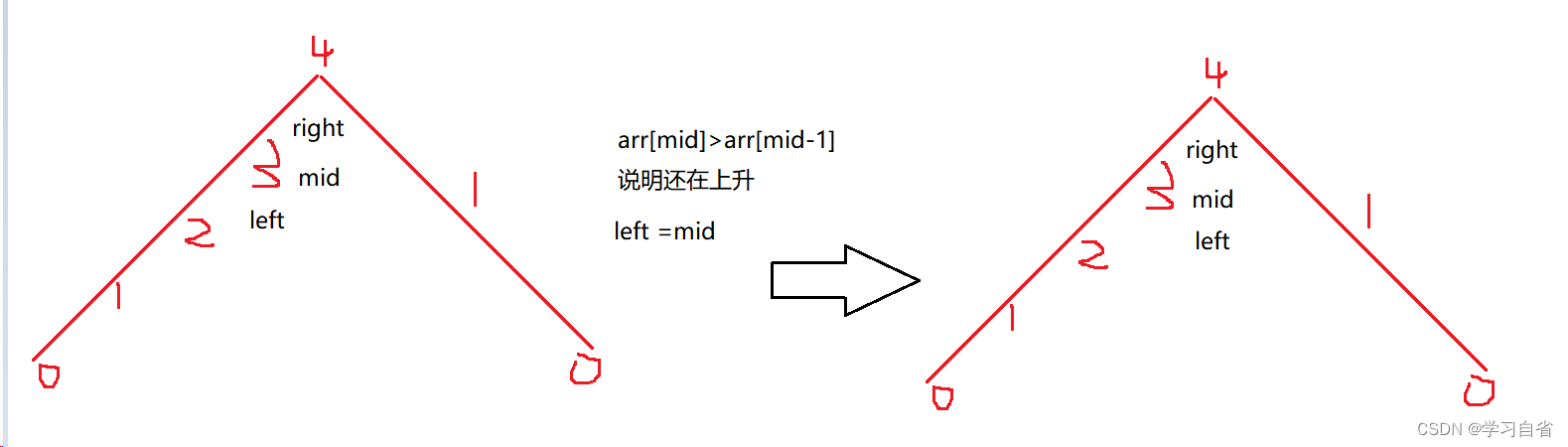
代码:
public int peakIndexInMountainArray(int[] arr) {int left=0,right=arr.length-2;while(left<right){//靠右取条件int mid=left+(right-left+1)/2;//数组遵循大体就是 /\// / \// / \ 在一定区间内有二段性 //所以每次目标值都是mid-1的位置if(arr[mid]>arr[mid-1])left=mid;//如果小于说明right 太大了else right=mid-1;}return left;}2.4、0-n-1中缺失的数字
这个暂时在leetcode上没有找到合适的,友友们作为练手,leetcode上有些题有些变动,原来是有的,现在可以能题目名字变了
1 2 3 4 5 6 8 9 10 少了个7
注:其实这里普通二分法也能解决问题,这里没有用普通二分,使用找左端点的二分法
代码:
public static void main(String[] args) {int[] nums={0,1,2,3,4,5,6,7,8,9,10};System.out.println(missingNumber(nums));}public static int missingNumber(int[] nums){int left = 0, right = nums.length-1;while(left<right){//靠左条件int mid = left + (right-left)/2;if(nums[mid]==mid){left=mid+1;}else {right=mid;}}//如果找到了 小的了 说明缺下一个位置 left+1 return nums[left]==left?left+1:left;}