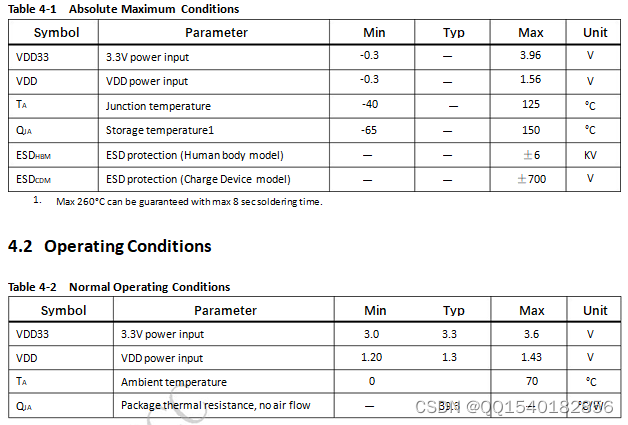
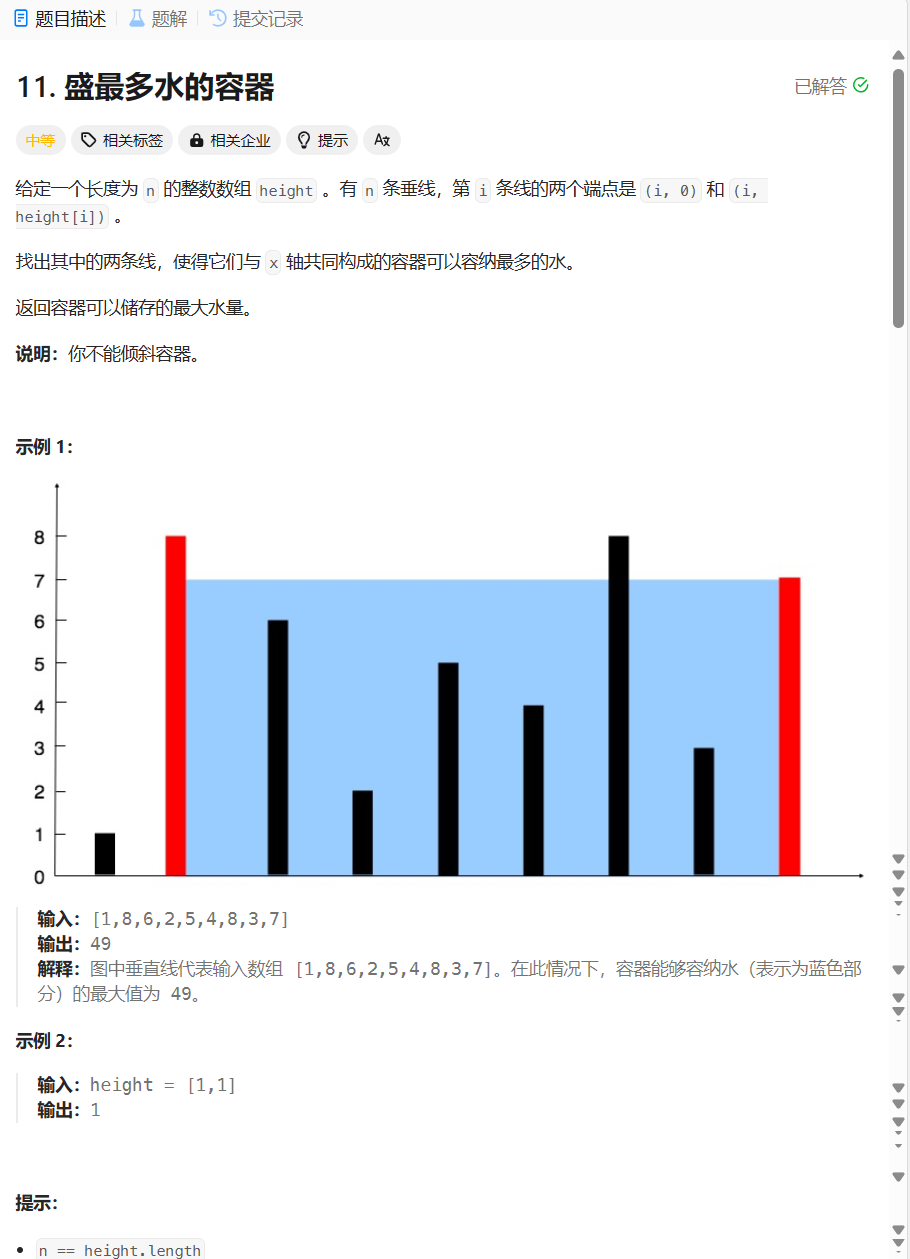
1.题目

2.算法思路

有两种方法：

第一种：

暴力穷举法，就是用两次循环将所有的可能性算出来，然后求出最大值。

这种方法最容易想到，但时间复杂度是O(n^2)，一定会超时的！

第二种：

仔细观察题目特点，任意两条线之间的体积=短的那条线*两条线之间的距离。

例如数组{2，3，8，1，7，6}。2和6之间的距离=2*5。根据体积的计算特点，对于2来说，它和其他数字之间的体积一定小于2和6之间的体积，所以这些情况就可以直接舍掉，最大体积一定在{3,8,1,7,6}中产生。同样的道理，3和6之间的体积为3*4。对于3来说，它和其他数之间的体积一定小于3和6之间的体积，然后这些情况可以舍掉，只用考虑{8,1,7,6}。这样循环往复，最后的最大值一定在计算出来的体积中产生。

3.提交结果和代码实现

代码：

class Solution {
public:int maxArea(vector<int>& height) {int right=height.size()-1,left=0,max_sum=0;while(right!=left){int sum=min(height[left],height[right])*(right-left);max_sum=max(max_sum,sum);if(height[right]>height[left]) left++;else right--;}return max_sum;}
};

时间复杂度分析：

只遍历了一次数组，所以时间复杂度：O（n）。

空间复杂度分析：

定义了四个变量，所以空间复杂度：O（1）。