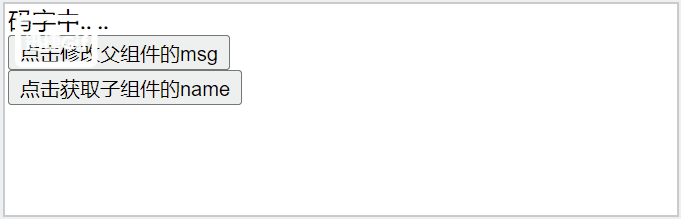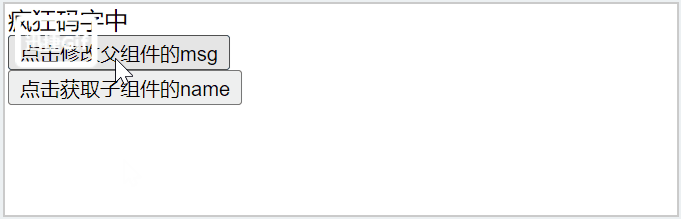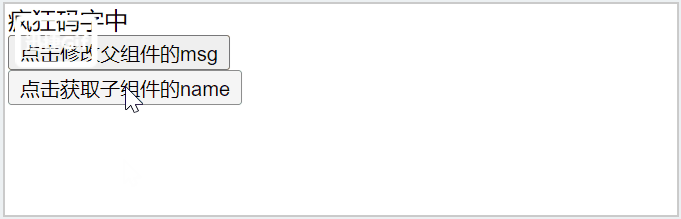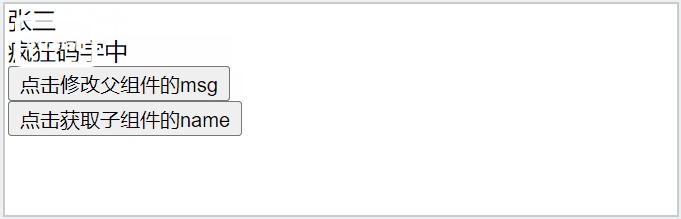
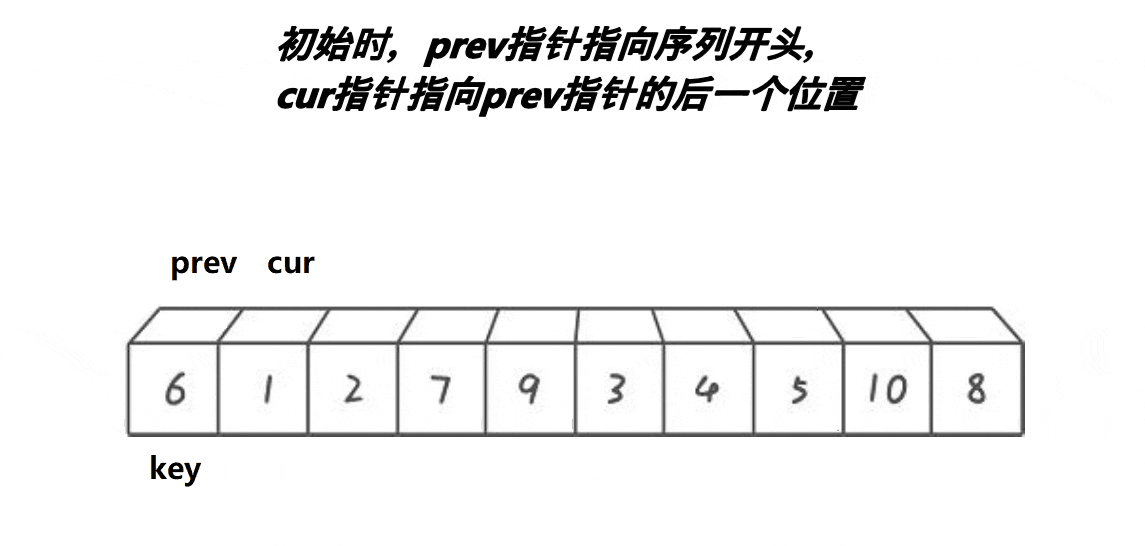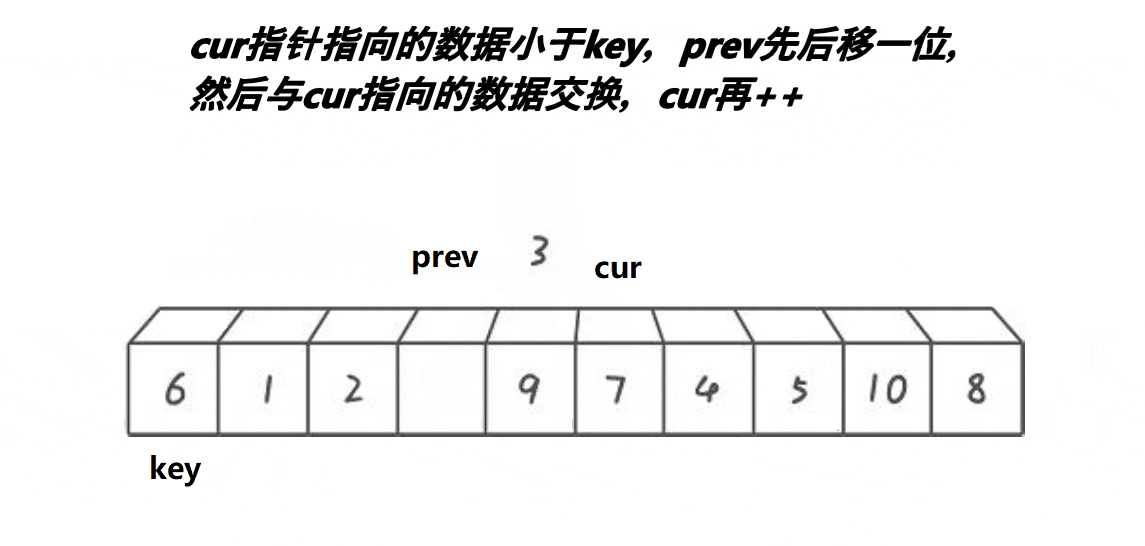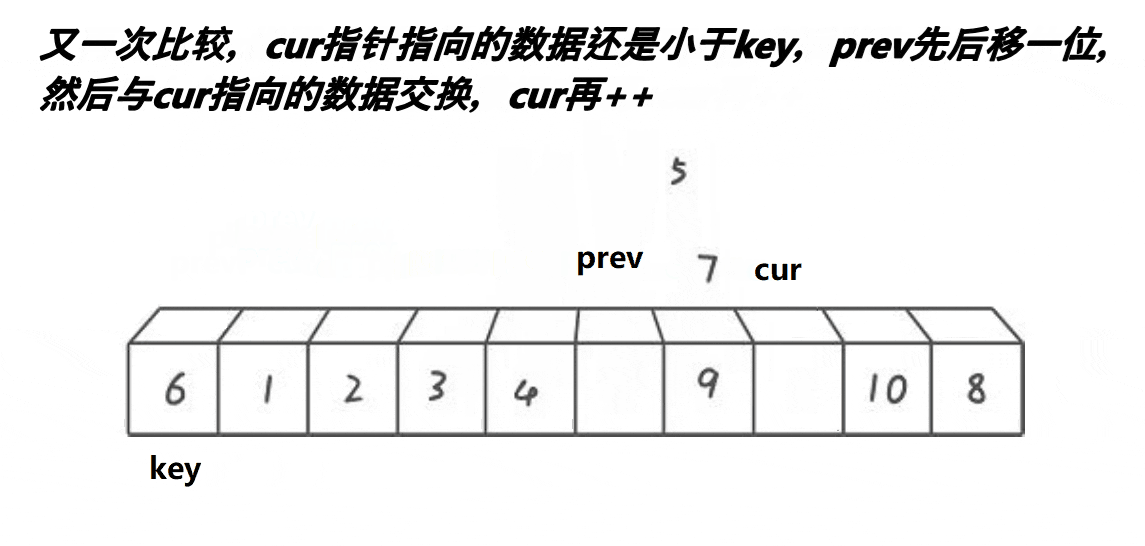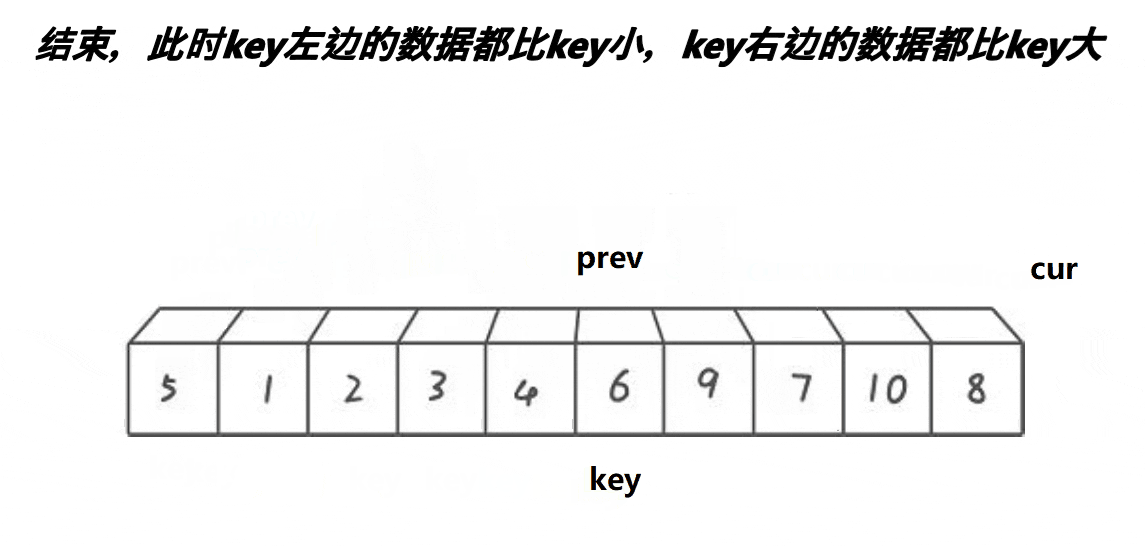
3.5 pillbox Cavity

从之前的知识我们可以知道，在空心的波导中，电磁场的模式是“离散”的，只有特定模式能够传播，并且与波导的几何形状和尺寸相关。

在RF高频腔设计（2）中，从传播常数k的图中可以看到传播常数k是连续的。

如果在波导的前后加上封闭的导体，则波导就变成了腔。此时传播常数也同样会变成离散的。

k对应着频率，因此腔中的频率也是离散的。

换句话说，在RF高频腔中只存在离散频率的稳定的电磁场。

这些离散的频率称为特征频率。

以矩形波导截断为“鞋盒”形状的腔为例：
离散的角频率满足如下等式：
$$\frac{{\omega }_{m,n,p}}{c}=\sqrt{{\left(\frac{m\pi }{a}\right)}^2+{\left(\frac{n\pi }{b}\right)}^2+{\left(\frac{p\pi }{\ell }\right)}^2}$$
圆形波导截断后就是pillbox腔，它的TM模式的角频率满足如下等式：
$$\frac{{\omega }_{m,n,p}}{c}=\sqrt{{\left(\frac{{\chi }_{m,n}}{a}\right)}^2+{\left(\frac{p\pi }{\ell }\right)}^2}$$
pillbox的名称可以看出它的轴向长度比较短。
当m=p=0，n=1则为TM010模式。

基模TM010的pillbox腔的轴向长度$l<2.03076R$

频率为：
$\frac{{\omega }_{0,\text{pillbox}}}{c}=\frac{{\chi }_{01}}{a}\approx \frac{2.40483}{a}$

TM010的pillbox电场和磁场为：
$$E_z=\frac{1}{j{\omega }_0{\epsilon }_0}\frac{{\chi }_{01}}{a}\sqrt{\frac{1}{\pi }}\frac{J_0\left({\chi }_{01}\frac{\rho }{a}\right)}{a{J}_1({\chi }_{01})},B_{\phi }={\mu }_0\sqrt{\frac{1}{\pi }}\frac{J_0\left({\chi }_{01}\frac{\rho }{a}\right)}{a{J}_1({\chi }_{01})}$$

TM010的截止频率也就是圆波导的TM01的截止频率。

下面是理想的pillbox腔怎么演变为实际的pillbox腔

理想的pillbox腔 --> 添加束流管道 --> 在束流管道和pillbox的腔交界处添加圆角（削弱交界处过大的场强）

当然大多数实际的腔并不像pillbox腔，但它们通常都是轴向对称的，并且有一个束流管道。

下面是一个re-entrant腔的四分之一的横截面图和它的基模。

pillbox腔的形状比较简单，因此我们可以通过计算得到pillbox腔的电磁场，但是通常情况下我们是很难计算高频腔电磁场的解析解，通常我们通过super fish、HFSS或者CST microwave studio等仿真工具计算它们的数值解。

3.6 加速电压

加速电压被定义：沿着粒子轨道的轴向电场的积分：
$$V_{\mathrm{acc}}=\int E_z{\mathrm{e}}^{-j\frac{\omega z}{\beta c}}\mathrm{d}z$$

其中$\beta c$为粒子的速度，c为光速。

上述的加速电压的公式考虑到了粒子的速度为有限速度，因此它在加速间隙中加速时，由于它的速度是有限的，而加速场也是随时间变化的，因此它在每个点看到加速电场是略有不同的，上面公式的指数项说明了这种变化。

那么假如有一个速度无限大的粒子，那么它穿过加速间隙时看到的加速场就是恒定的。
因此我们定义一个渡越时间因子（Transit Time）：
$$TT=\frac{\left|{\int }_{}^{}{E}_z{\mathrm{e}}^{-j\frac{\omega z}{\beta c}}\mathrm{d}z\right|}{{\int }_{}^{}\left|E_z\right|\mathrm{d}z}$$

其中分母部分是一个速度无限大的粒子穿过时获得的加速电压。

计算Pillbox的TT因子为：
$$T{T}_{\text{pillbox}}=\frac{\left|\sin \left(\frac{{\chi }_{01}\ell }{2a}\right)\right|}{\frac{{\chi }_{01}\ell }{2a}}$$
其中${\chi }_{01}$为0阶贝塞尔函数的第一个零点，对应TM010模式。

$l$是腔的加速间隙的长度。

从公式中我们可以看到，如果$l$趋于无穷小，则$\sin \left(\frac{{\chi }_{01}\ell }{2a}\right)\approx \frac{{\chi }_{01}\ell }{2a}$，因此$T{T}_{pillbox}=1$。也就是说粒子穿越时间无穷小，此时和速度无穷大的虚拟粒子获得的加速电压是一样的。
将上面的公式上下同时除以$\beta \lambda$则有
$$T{T}_{\text{pillbox}}=\frac{\left|\sin \left(\frac{{\chi }_{01}\ell }{2a\beta \lambda }\right)\right|}{\frac{{\chi }_{01}\ell }{2a\beta \lambda }}$$
$\beta \lambda$表示相对速度与波长的乘积
相对速度是粒子速度与光速即电磁波速度的比值。

可以这么理解，一个人在A列车上看另一个坐在光速的B列车上的另一个人的表演，表演的时长为加速场的波长，如果两列车都是光速，则他可以完整地看完表演，则粒子看到的波长为加速场本来的波长，如果A列车的速度小于光速，则他不能看完整个表演，也就是粒子看到的波长要比加速场原本的波长要短。

这个乘积的意义可以用来表征粒子看到加速场的相移。

因此我们可以绘制出TT时间因子相对于腔长与相移比的曲线。

从图中可以看到，当$\frac{l}{\beta \lambda }=1、2、\mathrm{3...}$时,表示粒子经历了加速场的整数倍的一个周期的相位变化，即粒子在腔中经历的加速时间和减速时间相等，此时渡越时间因子为0，即粒子获得的加速电压为0。

3.7 腔的储能

高频腔中的电场和磁场的相位相差90°，能量不断地在电能和磁能之间交换，因此就平均而言，电能和磁能是相等的。
下面是单个模式的能量表达式：
$$W=W_{\mathrm{E}}+W_{\mathrm{M}}=\iiint \frac{\epsilon }{2}|E{|}^2\mathrm{d}V+\iiint \frac{\mu }{2}|H{|}^2\mathrm{d}V$$

定义 R 比 Q (R upon Q)
$$\frac{R}{Q}=\frac{|V_{\mathrm{acc}}{|}^2}{2{\omega }_{0}W}$$

$\frac{R}{Q}$应该看作一个独立的属性变量，而不应该从它的名称意会为其它属性变量的派生变量。

这是因为$\frac{R}{Q}$仅仅与腔体的形状相关。

考虑最简单的情况，理想的pillbox腔的R/Q可以根据其电场和磁场的方程计算它的解析表达式，步骤如下：
pillbox的电磁场方程为
$$E_z=\frac{1}{j{\omega }_0{\epsilon }_0}\frac{{\chi }_{01}}{a}\sqrt{\frac{1}{\pi }}\frac{J_0\left({\chi }_{01}\frac{\rho }{a}\right)}{a{J}_1({\chi }_{01})},B_{\phi }={\mu }_0\sqrt{\frac{1}{\pi }}\frac{J_0\left({\chi }_{01}\frac{\rho }{a}\right)}{a{J}_1({\chi }_{01})}$$
代入能量表达式，再代入加速电压的表达式，最后将pillbox的能量表达式和加速电压表达式代入R/Q的表达式得到pillbox的R/Q的解析解如下：
$${\frac{R}{Q}}_{\text{pillbox}}=\frac{4\eta }{{\chi }_{01}^3\pi J_1^2({\chi }_{01})}\frac{{\sin }^2\left(\frac{{\chi }_{01}}{2}\frac{\ell }{a}\right)}{\frac{\ell }{a}}$$

其中$\eta =\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}=376.73\Omega$，定义为自由空间的波阻抗。