Leetcode 第394场周赛问题和解法-编程知识

题目

统计特殊字母的数量 I

给你一个字符串word。如果word中同时存在某个字母的小写形式和大写形式，则称这个字母为特殊字母。

返回word中特殊字母的数量。

示例 1:

输入：word = "aaAbcBC"输出：3解释：word 中的特殊字母是 'a'、'b' 和 'c'。

解题思路

创建两个数组，如果对应字母有出现过就置为1，然后再判断即可。

class Solution {public int numberOfSpecialChars(String word) {int[]count=new int[26];int[]bigCount=new int[26];int len=word.length();for(char mid:word.toCharArray()){if (mid>='a'&&mid<='z'){count[mid-'a']=1;}if (mid>='A'&&mid<='Z'){bigCount[mid-'A']=1;}}int res=0;for(int i=0;i<26;i++){if (count[i]==1&&bigCount[i]==1){res++;}}return res;}
}

统计特殊字母的数量 II

给你一个字符串word。如果word中同时出现某个字母c的小写形式和大写形式，并且每个小写形式的c都出现在第一个大写形式的c之前，则称字母c是一个特殊字母。

返回word中特殊字母的数量。

示例 1:

输入：word = "aaAbcBC"输出：3解释：特殊字母是 'a'、'b' 和 'c'。

解题思路

本题是第一题的变种，针对小写字母需要统计出现下标最大的值；针对大写字母需要统计出现下标最小的值，然后依次判断即可。

class Solution {public int numberOfSpecialChars(String word) {int[]count=new int[26];Arrays.fill(count,Integer.MIN_VALUE);int[]bigCount=new int[26];Arrays.fill(bigCount,Integer.MAX_VALUE);int len=word.length();char[]ca=word.toCharArray();for(int i=0;i<len;i++){if (ca[i]>='a'&&ca[i]<='z'){count[ca[i]-'a']=Math.max(i,count[ca[i]-'a']);}if (ca[i]>='A'&&ca[i]<='Z'){bigCount[ca[i]-'A']=Math.min(i,bigCount[ca[i]-'A']);}}int res=0;for(int i=0;i<26;i++){if (count[i]<bigCount[i]&&count[i]!=Integer.MIN_VALUE&&bigCount[i]!=Integer.MAX_VALUE){res++;}}return res;}
}

使矩阵满足条件的最少操作次数

给你一个大小为mxn的二维矩形grid。每次操作中，你可以将任一格子的值修改为任意非负整数。完成所有操作后，你需要确保每个格子grid[i][j]的值满足：

如果下面相邻格子存在的话，它们的值相等，也就是grid[i][j]==grid[i+1][j]（如果存在）。
如果右边相邻格子存在的话，它们的值不相等，也就是grid[i][j]!=grid[i][j+1]（如果存在）。

请你返回需要的最少操作数目。

示例 1：

输入：grid = [[1,0,2],[1,0,2]]输出：0解释：矩阵中所有格子已经满足要求。

在这里插入图片描述

解题思路

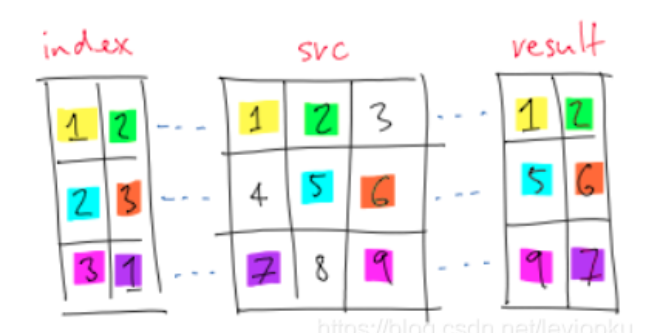
1.创建一个二维数组count. count[i][j]代表第i列有多少个数字j
2.遍历grid填充count数组
3.创建一个result数组, result[i][j]代表当第i列全部为数字j, 并且第0列当第i列所有数据都满足矩阵条件需要花费的最少操作次数
4.初始化第一列, result[0][i] = n - count[0][i];
5.每一列都只依赖前一列, 当前列可以为0-9的任意一个数字, 前一列的数字只要和当前列的数字不一样即可
那么result[i][x] = Math.min(result[i][x], (n - count[i][x]) + result[i - 1][y]);
6.最后我们只要查看最后一列为0-9需要花费的操作次数, 选择最小的即可

class Solution {public int minimumOperations(int[][] grid) {int n = grid.length;int m = grid[0].length;int[][] count = new int[m][10];for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){count[j][grid[i][j]] += 1;}}int[][] result = new int[m][10];for(int i = 0; i < m; i++){Arrays.fill(result[i], 0x3f3f3f3f);}for(int i = 0; i <= 9; i++){result[0][i] = n - count[0][i];}for(int i = 1; i < m; i++){for(int x = 0; x <= 9; x++){for(int y = 0; y <= 9; y++){if(x == y){continue;}result[i][x] = Math.min(result[i][x], (n - count[i][x]) + result[i - 1][y]);}}}int finalResult = 0x3f3f3f3f;for(int i = 0; i <= 9; i++){finalResult = Math.min(finalResult, result[m - 1][i]);}return finalResult;}}

最短路径中的边

给你一个n个节点的无向带权图，节点编号为0到n-1。图中总共有m条边，用二维数组edges表示，其中edges[i]=[ai,bi,wi]表示节点ai和bi之间有一条边权为wi的边。

对于节点0为出发点，节点n-1为结束点的所有最短路，你需要返回一个长度为m的boolean数组answer，如果edges[i]至少在其中一条最短路上，那么answer[i]为true，否则answer[i]为false。

请你返回数组answer。

注意，图可能不连通。

示例 1：

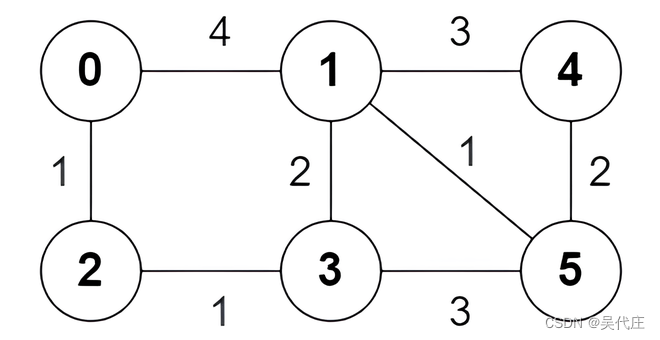
输入：n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]输出：[true,true,true,false,true,true,true,false]解释：以下为节点 0 出发到达节点 5 的 所有 最短路：路径 0 -> 1 -> 5 ：边权和为 4 + 1 = 5 。
路径 0 -> 2 -> 3 -> 5 ：边权和为 1 + 1 + 3 = 5 。
路径 0 -> 2 -> 3 -> 1 -> 5 ：边权和为 1 + 1 + 2 + 1 = 5 。

在这里插入图片描述

解题思路

首先用 Dijkstra 算法(堆优化版本)计算出起点0到所有节点的最短路长度dis.
如果 dis[n -1] = ∞，说明无法从起点0到终点n-1，答案全为false。
否则，我们可以从终点n-1出发，倒着 DFS 或 BFS，设当前在点y，邻居为x，边权为 w，如果满足dis[x] + w = dis[y]则说明 x-y 这条边在从0到n-1的最短路上。

class Solution {public boolean[] findAnswer(int n, int[][] edges) {List<int[]>[] g = new ArrayList[n];Arrays.setAll(g, i -> new ArrayList<>());for (int i = 0; i < edges.length; i++) {int[] e = edges[i];int x = e[0], y = e[1], w = e[2];g[x].add(new int[]{y, w, i});g[y].add(new int[]{x, w, i});}long[] dis = new long[n];Arrays.fill(dis, Long.MAX_VALUE);dis[0] = 0;PriorityQueue<long[]> pq = new PriorityQueue<>((a, b) -> Long.compare(a[0], b[0]));pq.offer(new long[]{0, 0});while (!pq.isEmpty()) {long[] dxPair = pq.poll();long dx = dxPair[0];int x = (int) dxPair[1];if (dx > dis[x]) {continue;}for (int[] t : g[x]) {int y = t[0];int w = t[1];long newDis = dx + w;if (newDis < dis[y]) {dis[y] = newDis;pq.offer(new long[]{newDis, y});}}}boolean[] ans = new boolean[edges.length];// 图不连通if (dis[n - 1] == Long.MAX_VALUE) {return ans;}// 从终点出发 BFSboolean[] vis = new boolean[n];dfs(n - 1, g, dis, ans, vis);return ans;}private void dfs(int y, List<int[]>[] g, long[] dis, boolean[] ans, boolean[] vis) {vis[y] = true;for (int[] t : g[y]) {int x = t[0];int w = t[1];int i = t[2];if (dis[x] + w != dis[y]) {continue;}ans[i] = true;if (!vis[x]) {dfs(x, g, dis, ans, vis);}}}
}