---

1.在排序数组中查找元素的第一个和最后一个位置

1.题目链接

• 在排序数组中查找元素的第一个和最后一个位置

---

2.算法原理详解

1.查找区间左端点

• 令中间值为x，目标值为t
• 如何迭代？
  • x < t -> left = mid + 1 -> [left, right]
  • x >= t -> right = mid -> [left, right]
• 细节处理：
  • 循环条件：left < right
  • 求中点方式：left + (right - left) / 2 -> 向下取整
• 循环条件为什么不能包含left == right？
  • left == right的时候，就是最终结果，无需判断
  • 如果判断，就会陷入死循环
    • 如果最后一次判断条件为x < t -> left = mid + 1 -> [left, right]
      • 则没问题，正常结束
    • 如果最后一次判断条件为x >= t -> right = mid -> [left, right]
      • 则会一直right = mid，陷入死循环
• 求中点方式为什么是left + (right - left) / 2？
  • 偶数时：求的是左端点
  • 如果最后一次判断条件为x < t -> left = mid + 1 -> [left, right]
    • 则没问题，正常结束
  • 如果最后一次判断条件为x >= t -> right = mid -> [left, right]
    • 则会一直right = mid，陷入死循环
      ![[Pasted image 20240327221405.png]]

2.查找区间右端点

• 令中间值为x，目标值为t
• 如何迭代？
  • x <= t -> left = mid -> [left, right]
  • x > t -> right = mid - 1 -> [left, right]
• 细节处理：
  • 循环条件：left < right
  • 求中点方式：left + (right - left + 1) / 2 -> 向上取整
• 循环条件为什么不能包含left == right？
  • left == right的时候，就是最终结果，无需判断
  • 如果判断，就会陷入死循环
    • 如果最后一次判断条件为x > t -> right = mid - 1 -> [left, right]
      • 则没问题，正常结束
    • 如果最后一次判断条件为x <= t -> left = mid -> [left, right]
      • 则会一直left = mid，陷入死循环
• 求中点方式为什么是left + (right - left + 1) / 2？
  • 偶数时：求的是右端点
  • 如果最后一次判断条件为x > t -> right = mid - 1 -> [left, right]
    • 则没问题，正常结束
  • 如果最后一次判断条件为x <= t -> left = mid -> [left, right]
    • 则会一直left = mid，陷入死循环
      

---

3.代码实现

vector<int> searchRange(vector<int>& nums, int target) 
{// 处理边界情况if(nums.size() == 0){return {-1, -1};}// 二分左端点int left = 0, right = nums.size() - 1;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] < target){left = mid + 1;}else{right = mid;}}int begin = 0;if(nums[left] == target){begin = left; // 标记左端点}else{return {-1, -1};}// 二分右端点// 这里其实left可以不做处理，算一个小优化left = 0, right = nums.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(nums[mid] <= target){left = mid;}else{right = mid - 1;;}}return {begin, right};
}

---

2.x 的平方根

1.题目链接

• x 的平方根

---

2.算法原理详解

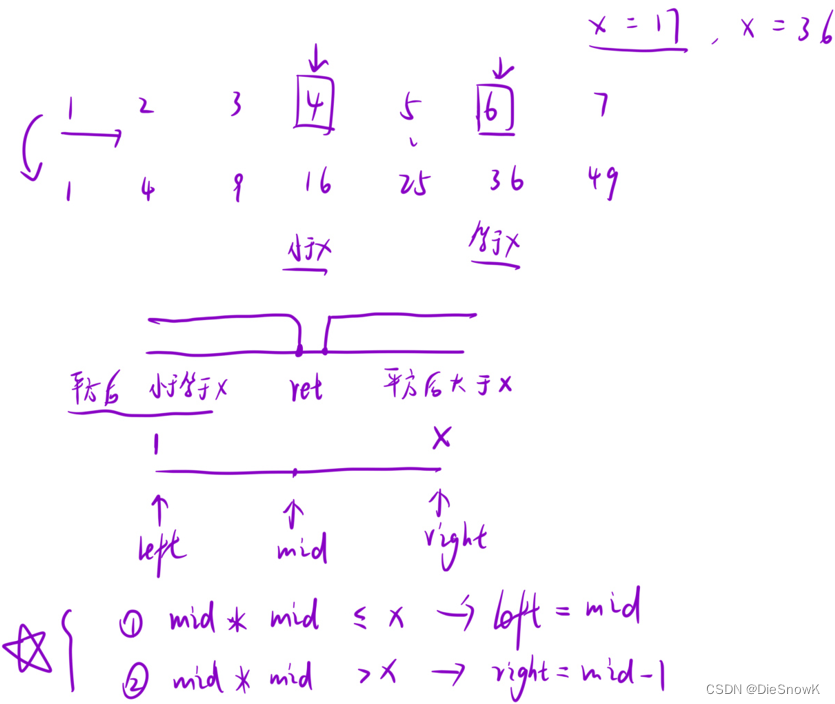
• 本题虽然可以直接遍历求值，但是时间复杂度为O(N)，显然效率不高
• 可以把问题抽象成，在数组$[1,x]$内，找x的平方根
  • 此时，数组具有二段性，可以用二分查找
    

---

3.代码实现

int MySqrt(int x) 
{// 处理边界情况if(x < 1){return 0;}int left = 1, right = x;while(left < right){long long mid = left + (right - left + 1) / 2;if(mid * mid <= x){left = mid;}else{right = mid - 1;}}return left;
}