XYK欺诈检测简介-编程知识

1. 背景

用30w左右的信用卡欺诈数据集测试下IF，看看每个参数的选择对最后结果的影响。信用卡欺诈是指故意使用伪造、作废的信用卡，冒用他人的信用卡骗取财物，或用本人信用卡进行恶意透支的行为，信用卡欺诈形式分为3种：

1. 伪造信用卡，占比60%+，其特点是团伙性质，从盗取卡资料、制造假卡、贩卖假卡，到用假卡作案，牟取暴利；

2. 失卡冒用；

3. 假冒申请。

1.1 数据介绍

数据来自于kaggle上的一个信用卡欺诈检测比赛，数据质量高，正负样本比例非常悬殊，很典型的异常检测数据集，在这个数据集上来测试一下各种异常检测手段的效果。

异常检测模型的评估，由于黑白样本极度不平衡，不适合使用准确率。

该数据集包含欧洲持卡人于 2013年9月通过信用卡进行的交易信息。此数据集显示的是两天内发生的交易，在284807笔交易中，存在492起欺诈，数据集高度不平衡，正类(欺诈)仅占所有交易的 0.172%。原数据集已做脱敏处理和PCA处理，匿名变量 V1,V2,..., V28 是 PCA 获得的主成分，唯一未经过 PCA 处理的变量是 Time 和 Amount。项目要求根据现有数据集建立分类模型，对信用卡欺诈行为进行检测。

1. Time: 每笔交易与数据集中第一笔交易之间的间隔，单位为秒；

2. Amount 是交易金额。

3. Class 是分类变量，在发生欺诈时为1，否则为0。

4. PCA(Principal Component Analysis) 用于提取数据集的"主成分"特征，即对数据集进行降维处理。

数据下载：https://www.kaggle.com/mlg-ulb/creditcardfraud

2. IF最佳参数选择

IF最重要的三个参数：

1. n_estimators：iTree的个数，默认为100个；
2. max_samples：用来训练随机树的样本数量，即子采样的大小，默认每次采样 256个；
3. max_features : 构建每个子树的特征数，指定从总样本中抽取来训练每棵iTree树的属性的数量，默认只使用 1个特征；

2.1 使用默认参数

from sklearn.ensemble import IsolationForest
data = pd.read_csv('data.csv')
data['Hour'] = data["Time"].apply(lambda x: divmod(x, 3600)[0])
X = data.drop(['Time', 'Class'], axis=1)
Y = data.Classiforest = IsolationForest()
data['label'] = iforest.fit_predict(X)
data['scores'] = iforest.decision_function(X)
# TopN准确率评估
n = 1000
df = data.sort_values(by='scores', ascending=True)
rate = df[df['Class'] == 1].shape[0]/n
print('Top{}的准确率为:{}'.format(n, rate))
# Top1000的准确率为:0.187

默认参数：

iforest.get_params()
{'n_estimators': 100,  'bootstrap': False,'max_samples': 'auto',  'max_features': 1.0,'contamination': 'auto', 'n_jobs': None,'random_state': None, 'verbose': 0, 'warm_start': False}

2.2 调整 max_features

每次构建树时候，抽取的特征个数，从1开始，本数据集有30个特征，做30次评估。这里把max_samples 设为1200，因为如果每次抽取的样本数过少，可能会出现“特征最多的时候，准确率最高”的情况；而实际上对于IF，当特征最大时，模型的相关性很高，融合准确率反而低。

可以看到：max_features在7左右能取到一个较好的值。其他两个参数也可以如此筛选。

2.3 最佳模型与可视化

1. 最佳模型

iforest = IsolationForest(n_estimators=250, max_samples=125000,contamination=0.05, max_features=5, random_state=1)

2. 模型可视化

from sklearn import tree
from dtreeviz.trees import dtreeviz
import graphviz n = 2 # 第n颗树可视化 dir(clf)
clf = iforest.estimators_[n]
names = [X.columns[i] for i in iforest.estimators_features_[n]]
dot_data = tree.export_graphviz(clf, out_file=None, feature_names=names, filled=True, rounded=True, special_characters=True)  
graph = graphviz.Source(dot_data)  
print(graph)

3. 用AE进行异常检测

基于深度学习AutoEncoder的欺诈异常检测，效果非常牛逼。

信用卡欺诈数据集，在IF上能做到26%的top1000准确率，而在AE上，达到了33.6%，但是这个数据很不稳定，有时候只有25%左右，至少说明这个模型潜力巨大，需要更多的试验，找到更稳定的网络结构。

3.1 AE简介

自编码器是一类在半监督和非监督学习中使用的人工NN，其功能是通过将输入信息作为学习目标，对输入信息进行表征学习(representation learning)，自编码器包含encoder和decoder两部分。

NN 通过大量数据集，进行end-to-end的训练，不断提高其准确率，而AE通过设计encoder和decoder 过程使输入和输出越来越接近，是一种无监督学习过程，可以被应用于降维和异常值检测，包含卷积层构筑的自编码器可被应用于CV问题，包括图像降噪、神经风格迁移等。

1. 用AE进行降噪: 通过卷积自编码器，降噪效果还是非常好的，最终生成的图片看起来非常顺滑，噪声也几乎看不到了。

2. 用AE进行降维:

3.2 AE 结构简介

AE使用一个NN来产生一个高维输入的低维表，与PCA类似，但AE在使用非线性激活函数时克服了PCA线性的限制。其中encoder的作用是用来对给定数据进行压缩表示，decoder是用来重建原始输入。在训练时，decoder 强迫AE选择最有信息量的特征，保存在压缩表示中。以下图为例，原始数据是10维，encoder和decoder分别有两层，中间的code有3个节点，即原始数据被降到了3维。Decoder根据降维后的数据再重建原始数据，重新得到10维的输出。从Input到Ouptut的这个过程中，AE实际上也起到了降噪的作用。

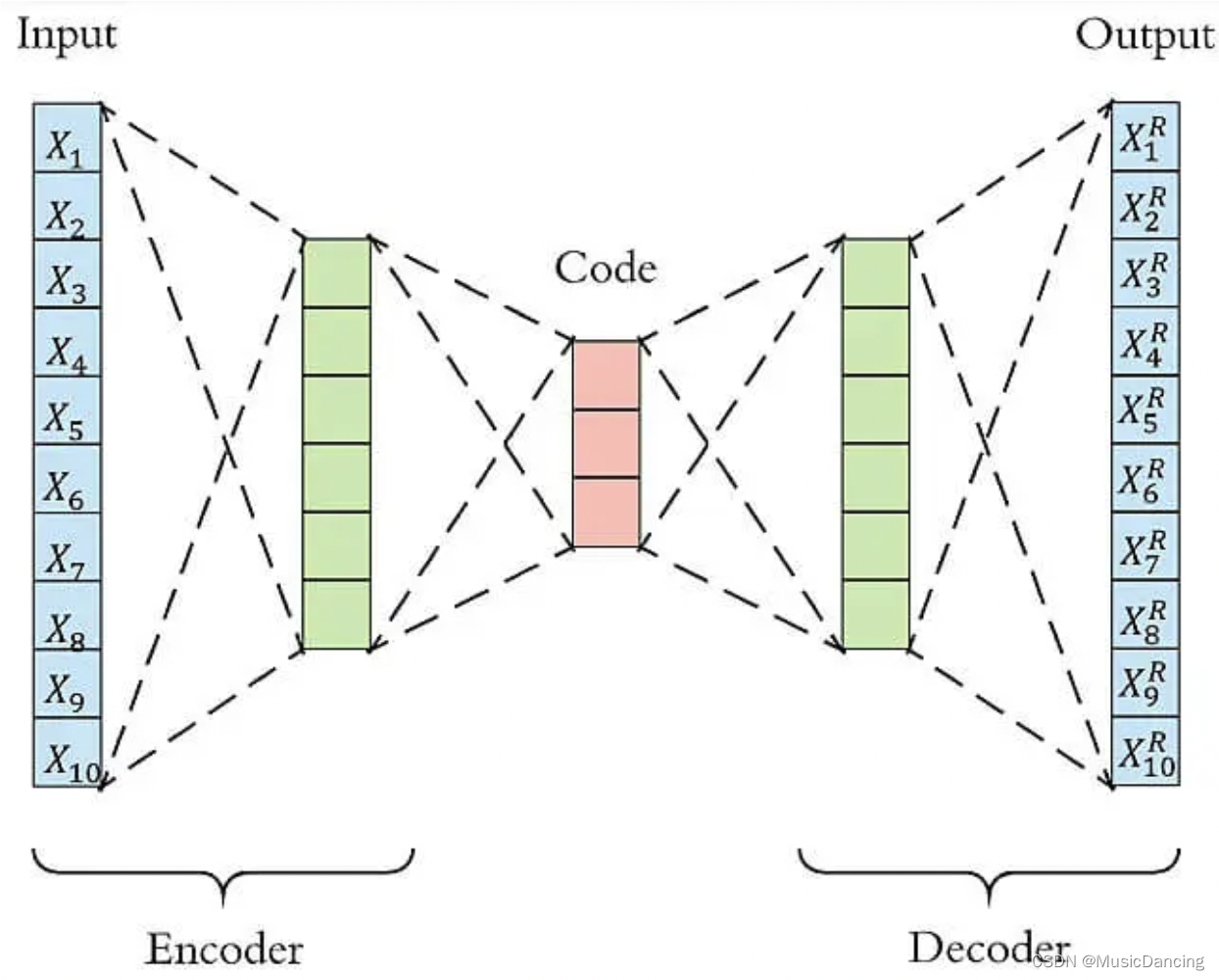
3.3 AE 异常检测流程

anomaly detection 通常分为有监督和无监督两种情形。在无监督的情况下，没有异常样本用来学习，算法假设是异常点服从不同的分布。根据正常数据训练出来的AE，能够将正常样本重建还原，但是却无法将异于正常分布的数据点较好地还原，导致还原误差较大。

如果样本的特征都是数值变量，可以用MSE或MAE作为还原误差。如上图，如果输入样本为

$X=(X_{1},X_{2},...,X_{10})$ ，经过AE重建后的结果为 $X^{R}=(X_{1}^{R},X_{2}^{R},...,X_{10}^{R})$ 。

其还原误差MSE为 $\frac{1}{10}\sum_{i=1}^{10}(X_{i}-X_{i}^{R})^{2}$ ，还原误差MAE为 $\frac{1}{10}\sum_{i=1}^{10}\left |X_{i}-X_{i}^{R} \right |$

3.4 模型算法过程

1. 数据加载

import tensorflow as tf
import seaborn as sns
from sklearn.model_selection import train_test_split
from keras.models import Model, load_model
from keras.layers import Input, Dense,LeakyReLU,BatchNormalization
from keras.callbacks import ModelCheckpoint
from keras import regularizers
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_curve, auc, precision_recall_curvedata = pd.read_csv('data.csv')
data = data.drop(['Time'], axis=1)
data['Amount'] = StandardScaler().fit_transform(data[['Amount']])  # 对Amount进行标准化
X = data.drop(['Class'], axis=1)
Y = data.Class

2. 模型搭建&模型训练

# 设置 AE 的参数
input_dim = X.shape[1]
encoding_dim = 128
num_epoch = 30
batch_size = 256
input_layer = Input(shape=(input_dim, ))# encoder
encoder = Dense(encoding_dim, activation="tanh",activity_regularizer=regularizers.l1(10e-5))(input_layer)
encoder = BatchNormalization()(encoder)
encoder = LeakyReLU(alpha=0.2)(encoder)
encoder = Dense(int(encoding_dim/2), activation="relu")(encoder)
encoder = BatchNormalization()(encoder)
encoder = LeakyReLU(alpha=0.1)(encoder)
encoder = Dense(int(encoding_dim/4), activation="relu")(encoder)
encoder = BatchNormalization()(encoder)
# decoder
decoder = LeakyReLU(alpha=0.1)(encoder)
decoder = Dense(int(encoding_dim/4), activation='tanh')(decoder)
decoder = BatchNormalization()(decoder)
decoder = LeakyReLU(alpha=0.1)(decoder)
decoder = Dense(int(encoding_dim/2), activation='tanh')(decoder)
decoder = BatchNormalization()(decoder)
decoder = LeakyReLU(alpha=0.1)(decoder)
decoder = Dense(input_dim,)(decoder)  # activation='relu'autoencoder = Model(inputs = input_layer, outputs = decoder)
autoencoder.compile(optimizer='adam', loss='mean_squared_error', metrics=['mae','mse'])
# 模型保存路径
checkpointer = ModelCheckpoint(filepath="ae_model.h5", verbose=0, save_best_only=True)
history = autoencoder.fit(X, X, epochs=num_epoch, batch_size=batch_size, shuffle=True,# validation_data=(X_test, X_test),verbose=1, callbacks=[checkpointer]).history

3. 模型结果可视化

画出损失函数曲线，mae、mse 亦是(替换loss即可)。

plt.figure(figsize=(14, 5))
plt.subplot(121)
plt.plot(history['loss'], c='dodgerblue', lw=3)
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper right')

4. 模型结果预测

autoencoder = load_model('ae_model.h5')
# 利用训练好的autoencoder重建测试集
pred_X = autoencoder.predict(X)
# 计算还原误差MSE和MAE
mse_X = np.mean(np.power(X-pred_X, 2), axis=1)
mae_X = np.mean(np.abs(X-pred_X), axis=1)
data['mse_X'] = mse_X
data['mae_X'] = mae_X
# TopN准确率评估
n = 1000
df = data.sort_values(by='mae_X', ascending=False)
rate = df[df['Class'] == 1].shape[0]/n
print('Top{}的准确率为:{}'.format(n, rate))
# Top1000的准确率为: 0.336

3.5 探索正负样本分布差异

1. 样本处理

X_train, X_test = train_test_split(X, test_size=0.3, random_state=520)
mask = (data['Class'] == 0)  # 提取负样本，0为正常样本，1为欺诈
X_fraud = X[~mask]  # 提取所有正样本，作为测试集的一部分

2. 利用训练好的AE重建测试集

pred_test = autoencoder.predict(X_test)
pred_fraud = autoencoder.predict(X_fraud)
# 计算还原误差MSE和MAE
mse_test = np.mean(np.power(X_test - pred_test, 2), axis=1)
mse_fraud = np.mean(np.power(X_fraud - pred_fraud, 2), axis=1)
mae_test = np.mean(np.abs(X_test - pred_test), axis=1)
mae_fraud = np.mean(np.abs(X_fraud - pred_fraud), axis=1)
mse_df = pd.DataFrame()
mse_df['Class'] = [0] * len(mse_test) + [1] * len(mse_fraud)
mse_df['MSE'] = np.hstack([mse_test, mse_fraud])
mse_df['MAE'] = np.hstack([mae_test, mae_fraud])
mse_df = mse_df.sample(frac=1).reset_index(drop=True)

3. 分别画出测试集中正样本和负样本的还原误差MAE和MSE

markers = ['o', '^']
colors = ['dodgerblue', 'coral']
labels = ['Non-fraud', 'Fraud']plt.figure(figsize=(14, 5))
plt.subplot(121)
for flag in [1, 0]:temp = mse_df[mse_df['Class'] == flag]plt.scatter(temp.index, temp['MAE'], alpha=0.7, marker=markers[flag], c=colors[flag], label=labels[flag])
plt.title('Reconstruction MAE')
plt.ylabel('Reconstruction MAE')
plt.xlabel('Index')plt.subplot(122)
for flag in [1, 0]:temp = mse_df[mse_df['Class'] == flag]plt.scatter(temp.index, temp['MSE'], alpha=0.7, marker=markers[flag], c=colors[flag], label=labels[flag])
plt.legend(loc=[1, 0], fontsize=12)
plt.title('Reconstruction MSE')
plt.ylabel('Reconstruction MSE')
plt.xlabel('Index')
plt.show()