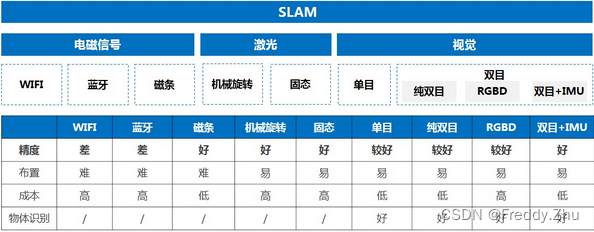
⭐️ 卡尔曼滤波

卡尔曼滤波（Kalman Filtering）是一种用于状态估计的强大技术，常用于处理具有随机噪声的系统的状态估计问题。在目标跟踪等应用中，卡尔曼滤波常被用来预测目标的位置和速度等状态变量，并根据观测数据进行状态更新，从而实现对目标轨迹的跟踪。

在目标跟踪中，可能会出现假点（False Positives）的情况，即目标跟踪算法错误地将背景中的噪声或其他物体错误地识别为目标。为了减少假阳性的影响，可以使用卡尔曼滤波器进行假点过滤。下面是卡尔曼滤波的基本原理：

状态模型： 假设目标的状态变量为 ${\mathbf{x}}_k$，包括位置、速度等信息。卡尔曼滤波器会根据系统的动力学模型来预测目标的下一个状态 ${\hat{\mathbf{x}}}_k^{-}$。通常采用线性动力学模型，形式为 ${\mathbf{x}}_k={\mathbf{F}}_k{\mathbf{x}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k+{\mathbf{w}}_k$，其中 ${\mathbf{F}}_k$ 是状态转移矩阵，${\mathbf{B}}_k$ 是控制输入矩阵，${\mathbf{u}}_k$ 是外部控制输入，${\mathbf{w}}_k$ 是过程噪声（高斯分布）。

观测模型： 卡尔曼滤波器会根据观测数据来更新状态估计值。假设观测数据为 ${\mathbf{z}}_k$，卡尔曼滤波器会根据观测模型 ${\mathbf{z}}_k={\mathbf{H}}_k{\mathbf{x}}_k+{\mathbf{v}}_k$ 来估计目标的位置。其中 ${\mathbf{H}}_k$ 是观测矩阵，${\mathbf{v}}_k$ 是观测噪声（高斯分布）。

卡尔曼滤波器更新： 卡尔曼滤波器利用预测值和观测值的差异，结合系统的动力学模型和观测模型，计算出最优的状态估计值。具体来说，卡尔曼滤波器包括两个主要步骤：

预测步骤（Predict）： 根据系统的动力学模型，预测目标的状态变量，并计算预测的状态协方差矩阵 ${\mathbf{P}}_k^{-}$。

更新步骤（Update）： 根据观测模型，计算卡尔曼增益 ${\mathbf{K}}_k$，并利用观测数据对预测值进行修正，得到最终的状态估计值 ${\hat{\mathbf{x}}}_k$ 和状态协方差矩阵 ${\mathbf{P}}_k$。

整体过程如下图所示：

卡尔曼的相关资料很多，更详细的知识，读者可以自行搜索，嘻嘻！！！

小编推荐一部著作《Kalman_and_Bayesian_Filters_in_Python》和一位大神的博客 【滤波】设计卡尔曼滤波器，这位大神对前面的著作做了整体的翻译，很牛！！！

⭐️ 设计个卡尔曼滤波器，估计机器人的位置

本文参考《Kalman_and_Bayesian_Filters_in_Python》中的案例，利用函数模拟机器人的位置，然后通过简单卡尔曼滤波器利用测量数据对机器人位置进行估计。

滤波器各个参数设计如下

状态：

状态转移方程：

状态转移矩阵：

观测矩阵：

初始测量误差协方差矩阵：

初始状态及其协方差矩阵：

过程误差协方差矩阵利用白噪声获取。

整体代码如下

from numpy.random import randn
import matplotlib.pyplot as plt
import numpy as np
from filterpy.kalman import KalmanFilter
from scipy.linalg import block_diag
from filterpy.common import Q_discrete_white_noise
from filterpy.stats import plot_covariance_ellipse# 模拟传感器，返回robot的位置信息
class PosSensor(object):def __init__(self, pos=(0, 0), vel=(0, 0), noise_std=1.):self.vel = velself.noise_std = noise_stdself.pos = [pos[0], pos[1]]def read(self):self.pos[0] += self.vel[0]self.pos[1] += self.vel[1]return [self.pos[0] + randn() * self.noise_std,self.pos[1] + randn() * self.noise_std]# 绘制过滤器输出数据
def plot_filter(xs, ys=None, dt=None, c='C0', label='Filter', var=None, **kwargs):if ys is None and dt is not None:ys = xsxs = np.arange(0, len(ys) * dt, dt)if ys is None:ys = xsxs = range(len(ys))lines = plt.plot(xs, ys, color=c, label=label, **kwargs)if var is None:return linesvar = np.asarray(var)std = np.sqrt(var)std_top = ys+stdstd_btm = ys-stdplt.plot(xs, ys+std, linestyle=':', color='k', lw=2)plt.plot(xs, ys-std, linestyle=':', color='k', lw=2)plt.fill_between(xs, std_btm, std_top, facecolor='yellow', alpha=0.2)return lines# 测量误差方差
R_std = 0.35
# 过程误差方差
Q_std = 0.04def tracker():# 创建卡尔曼滤波器tracker = KalmanFilter(dim_x=4, dim_z=2)# 时间步伐dt = 1.0# 状态转移矩阵tracker.F = np.array([[1, dt, 0,  0],[0,  1, 0,  0],[0,  0, 1, dt],[0,  0, 0,  1]])# 过程输入值tracker.u = 0.# 观测矩阵tracker.H = np.array([[1/0.3048, 0, 0, 0],[0, 0, 1/0.3048, 0]])# 测量误差协方差矩阵tracker.R = np.eye(2) * R_std**2# 白噪声q = Q_discrete_white_noise(dim=2, dt=dt, var=Q_std**2)# 过程噪声协方差矩阵tracker.Q = block_diag(q, q)# 初始状态tracker.x = np.array([[0, 0, 0, 0]]).T# 初始状态协方差矩阵tracker.P = np.eye(4) * 500.return tracker# 模拟机器人移动
N = 30
sensor = PosSensor((0, 0), (2, .5), noise_std=R_std)
# 测量数据，位置信息
zs = np.array([sensor.read() for _ in range(N)])# 运行过滤器
robot_tracker = tracker()
# 卡尔曼滤波结果
mu, cov, _, _ = robot_tracker.batch_filter(zs)for x, P in zip(mu, cov):# x 和 y 的协方差cov = np.array([[P[0, 0], P[2, 0]], [P[0, 2], P[2, 2]]])mean = (x[0, 0], x[2, 0])# 绘制卡尔曼滤波器输出的位置信息，包括位置和方差plot_covariance_ellipse(mean, cov=cov, fc='g', std=3, alpha=0.5)# 坐标位置转换为单位米
zs *= .3048
# 绘制测量数据和过滤器输出
plot_filter(mu[:, 0], mu[:, 2])
plt.scatter(zs[:, 0], zs[:, 1], color='k', facecolor='none', lw=2, label='Measurements'),
plt.legend(loc=2)
plt.xlim(0, 20)
plt.show()

运行结果如下

笔者水平有限，若有不对的地方欢迎评论指正！