作者:翟天保Steven
版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处
需求说明
一般用到FFT,就涉及到复数的计算,为了便于调用,我自行封装了一个简单的复数矩阵点乘函数。复数乘法公式:
下面展示代码。
功能函数
// 复数矩阵点乘
cv::Mat ComplexMatrixDotMultiplication(const cv::Mat& A, const cv::Mat& B)
{// 确保A和B都是双通道的矩阵CV_Assert(A.channels() == 2 && B.channels() == 2);// 提取A和B的实部和虚部std::vector<cv::Mat> A_channels, B_channels;cv::split(A, A_channels);cv::split(B, B_channels);cv::Mat A_real = A_channels[0];cv::Mat A_imag = A_channels[1];cv::Mat B_real = B_channels[0];cv::Mat B_imag = B_channels[1];// 计算相乘cv::Mat C_real = A_real.mul(B_real) - A_imag.mul(B_imag);cv::Mat C_imag = A_real.mul(B_imag) + A_imag.mul(B_real);// 合并结果std::vector<cv::Mat> C_channels{ C_real, C_imag };cv::Mat C;cv::merge(C_channels, C);return C;
}C++&Matlab测试代码
#include <iostream>
#include <time.h>
#include <opencv2/opencv.hpp>using namespace std;
using namespace cv;// 复数矩阵点乘
cv::Mat ComplexMatrixDotMultiplication(const cv::Mat& A, const cv::Mat& B)
{// 确保A和B都是双通道的矩阵CV_Assert(A.channels() == 2 && B.channels() == 2);// 提取A和B的实部和虚部std::vector<cv::Mat> A_channels, B_channels;cv::split(A, A_channels);cv::split(B, B_channels);cv::Mat A_real = A_channels[0];cv::Mat A_imag = A_channels[1];cv::Mat B_real = B_channels[0];cv::Mat B_imag = B_channels[1];// 计算相乘cv::Mat C_real = A_real.mul(B_real) - A_imag.mul(B_imag);cv::Mat C_imag = A_real.mul(B_imag) + A_imag.mul(B_real);// 合并结果std::vector<cv::Mat> C_channels{ C_real, C_imag };cv::Mat C;cv::merge(C_channels, C);return C;
}int main()
{// 定义实际数据的双通道矩阵 A 和 Bcv::Mat A = (cv::Mat_<std::complex<float>>)cv::Mat::zeros(4, 4, CV_32FC2);cv::Mat B = (cv::Mat_<std::complex<float>>)cv::Mat::zeros(4, 4, CV_32FC2);// 自定义 A 和 B 的数据for (int i = 0; i < A.rows; ++i) {for (int j = 0; j < A.cols; ++j) {A.at<std::complex<float>>(i, j) = std::complex<float>(i + 1, j + 1);B.at<std::complex<float>>(i, j) = std::complex<float>(i + 2, j + 2);}}// 调用复数矩阵乘法函数cv::Mat C = GlobalFunc::complexMatrixMultiplication(A, B);// 打印结果std::cout << "Result Matrix C:\n" << C << std::endl;return 0;
}
% 定义 A 和 B 的大小
rows = 4;
cols = 4;% 创建实际数据的双通道矩阵 A 和 B,初始值为零
A = zeros(rows, cols) + 1i * zeros(rows, cols);
B = zeros(rows, cols) + 1i * zeros(rows, cols);% 自定义 A 和 B 的数据
for i = 1:rowsfor j = 1:colsA(i, j) = complex(i, j);B(i, j) = complex(i + 1, j + 1);end
end% 复数矩阵点乘
C = A .* B;% 显示结果
disp('Result Matrix C:');
disp(C);测试效果
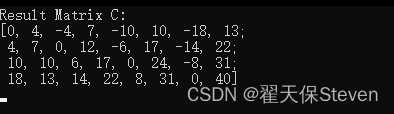

如果函数有什么可以改进完善的地方,非常欢迎大家指出,一同进步何乐而不为呢~
如果文章帮助到你了,可以点个赞让我知道,我会很快乐~加油!