目录
一、原理
1. 初始化Init
2. 查询 find
3. 合并 union
二、代码模板
三、练习
1、 990.等式方程的可满足性🟢
2、 1061. 按字典序排列最小的等效字符串🟢
3、721.账户合并 🟡
4、 839.相似字符串组🟡
5、 2812.找出最安全路径 🔴
一、原理
并查集主要运用与求一些不相交且有关联的集合的合并,这一点我们从后面的例题中进一步理解,我们首先掌握并查集的原理和运用
并查集的主要操作有:
1. 初始化Init
我们将每个数据看作一个树的节点,初始化每个节点指针指向自己
我们用一个数组fa[]的下标index表示节点, 用fa[index]表示该节点的根节点;
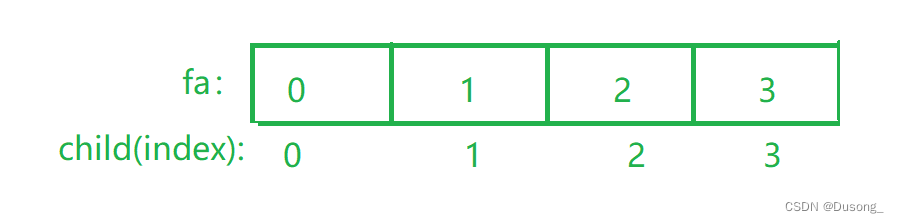
2. 查询 find
查询一个节点的根节点,以用于其他操作;
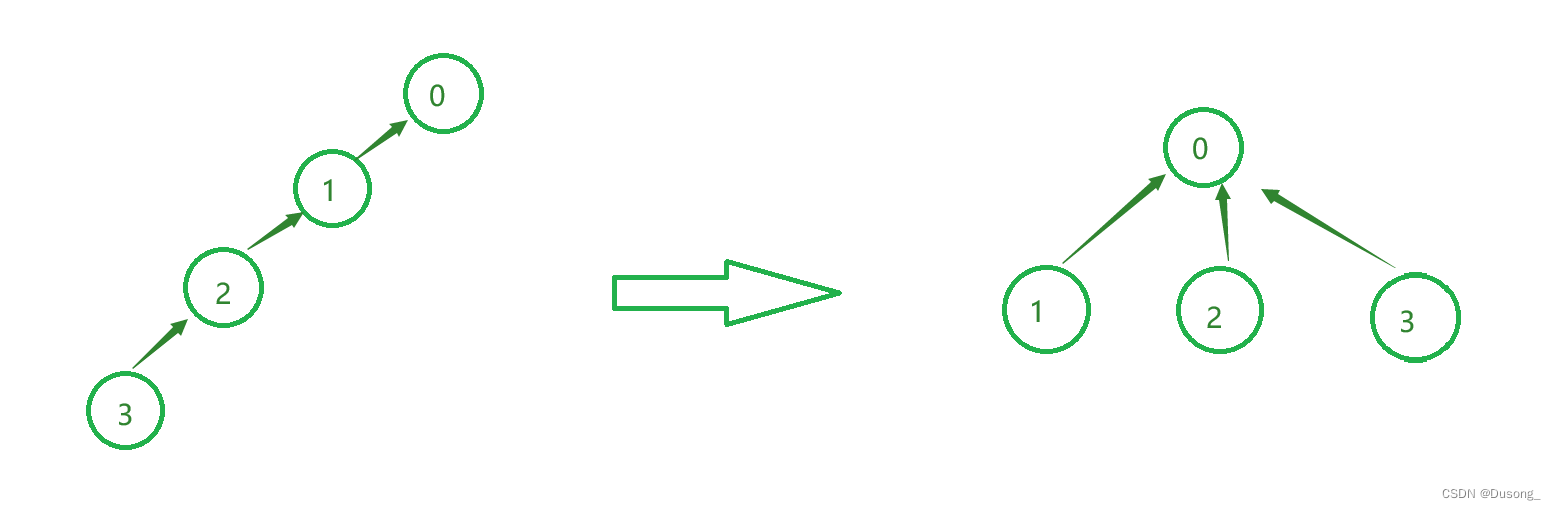
如上图, 若要查询数据3所在的集合的根节点,想做图这样的链接方式每次查询需要O(n)的时间,我们需要在查询时将树的结构转换成右图所示,这样之后的每次查询时间复杂度为O(logn)
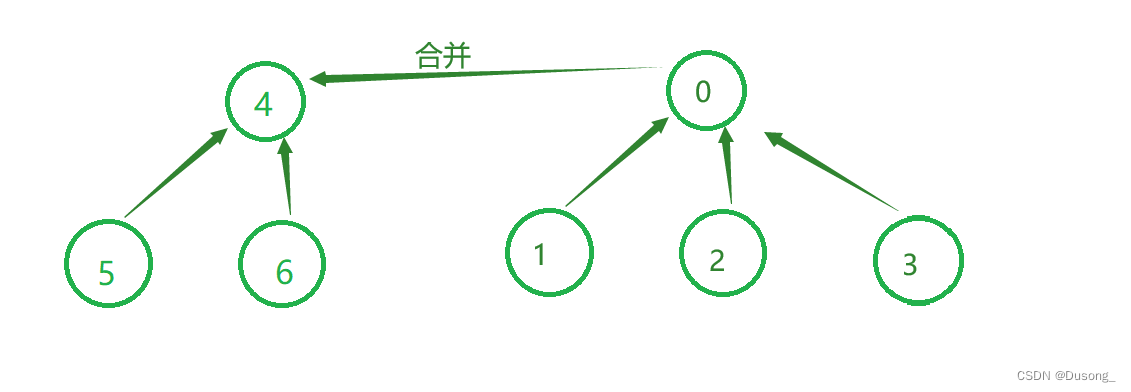
3. 合并 union
实现两个集合的合并,可以抽象成两颗树的合并,即将两颗树的根节点相连;
二、代码模板
//初始化
vector<int> fa(n* n);
iota(fa.begin(), fa.end(), 0);//查询
function<int(int)> find = [&](int x) -> int { return x == fa[x] ? x : fa[x] = find(fa[x]); }; //合并
fa[find(x)] = find(y); 三、练习
1、 990.等式方程的可满足性🟢
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程
equations[i]的长度为4,并采用两种不同的形式之一:"a==b"或"a!=b"。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回
true,否则返回false。
解题思路:合并等式方程两侧字母,运用并查集管理相等字母集合
class Solution {
public:bool equationsPossible(vector<string>& equations) {//初始化vector<int> fa(26);iota(fa.begin(), fa.end(), 0);//查询function<int(int)> find = [&](int x) -> int { return fa[x] == x ? x : fa[x] = find(fa[x]); };for (auto s : equations) {if (s[1] == '=') {int x = s[0] - 97, y = s[3] - 97;fa[find(x)] = find(y); //相等则合并}}for (auto s : equations) {int x = s[0] - 97, y = s[3] - 97;if (s[1] == '!' && find(x) == find(y)) return false; //矛盾,返回false}return true;}
};2、 1061. 按字典序排列最小的等效字符串🟢
给出长度相同的两个字符串
s1和s2,还有一个字符串baseStr。其中
s1[i]和s2[i]是一组等价字符。
- 举个例子,如果
s1 = "abc"且s2 = "cde",那么就有'a' == 'c', 'b' == 'd', 'c' == 'e'。等价字符遵循任何等价关系的一般规则:
- 自反性 :
'a' == 'a'- 对称性 :
'a' == 'b'则必定有'b' == 'a'- 传递性 :
'a' == 'b'且'b' == 'c'就表明'a' == 'c'例如,
s1 = "abc"和s2 = "cde"的等价信息和之前的例子一样,那么baseStr = "eed","acd"或"aab",这三个字符串都是等价的,而"aab"是baseStr的按字典序最小的等价字符串利用
s1和s2的等价信息,找出并返回baseStr的按字典序排列最小的等价字符串。
解题思路:由等价关系可以一眼看出这道题使用并查集,s1与s2对应字母放入一个集合(即将其合并),最终找到baseStr每个字母对应的集合中的最小字典序字母
class Solution {
public:string smallestEquivalentString(string s1, string s2, string baseStr) {//初始化vector<int> fa(26);iota(fa.begin(), fa.end(), 0);//查询function<int(int)> find = [&](int x) -> int { return fa[x] == x ? x : fa[x] = find(fa[x]); };for (int i = 0; i < s1.size(); i++) {int x = s1[i] - 97, y = s2[i] - 97;fa[find(y)] = find(x); //合并}unordered_map<int, set<char>> g; //统计以根节点代表的一个集合中的所有节点for (int i = 0; i < 26; i++) {g[find(i)].insert(i + 97);}for (int i = 0; i < baseStr.size(); i++) {//利用set默认排升序的特点,找到baseStr[i]的根节点的集合中的最小字母baseStr[i] = *(g[find(baseStr[i] - 97)].begin()); }return baseStr;}
};3、721.账户合并 🟡
给定一个列表
accounts,每个元素accounts[i]是一个字符串列表,其中第一个元素accounts[i][0]是 名称 (name),其余元素是 emails 表示该账户的邮箱地址。现在,我们想合并这些账户。如果两个账户都有一些共同的邮箱地址,则两个账户必定属于同一个人。请注意,即使两个账户具有相同的名称,它们也可能属于不同的人,因为人们可能具有相同的名称。一个人最初可以拥有任意数量的账户,但其所有账户都具有相同的名称。
合并账户后,按以下格式返回账户:每个账户的第一个元素是名称,其余元素是 按字符 ASCII 顺序排列 的邮箱地址。账户本身可以以 任意顺序 返回。
解题思路:根据题意,拥有相同邮箱的账户为同一人,最终需要将相同用户的邮箱合并到一起,同样也是一眼并查集,但是代码实现起来可能有些复杂;首先需要遍历所有邮箱,判断是否有重复,将拥有同一邮箱的用户合并,需要特别注意的是,用户名相同不代表是同一人,最终将属于同一集合的用户邮箱用set去重,返回结果;
class Solution {
public:vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {int n = accounts.size();//以accounts的下标[0, n)作为用户名字,方便以下标寻找父亲vector<int> fa(n);iota(fa.begin(), fa.end(), 0); //初始化function<int(int)> find = [&](int i) -> int { return fa[i] == i ? i : fa[i] = find(fa[i]); };//key:邮箱 val:名字unordered_map<string, vector<int>> email_name;for (int i = 0; i < n; i++) {for (int j = 1; j < accounts[i].size(); j++) { //遍历每个账户的所有邮箱email_name[accounts[i][j]].push_back(i);//如果同一个邮箱出现多个名字,那么认为为同一个人,此时连接if (email_name[accounts[i][j]].size() > 1) {fa[find(email_name[accounts[i][j]][0])] = find(i); //合并}}}//之前尝试用map,但是同一个名字可能不是同一人,所以map行不通//用set去重vector<set<string>> g(n);for (int i = 0; i < n; i++) {int f = find(i); //找到根节点,将邮箱插入到根节点的数组中for (int j = 1; j < accounts[i].size(); j++) {g[f].insert(accounts[i][j]); }}vector<vector<string>> ans;for (int i = 0; i < n; i++) {if (g[i].size() != 0) { vector<string> tmp = {g[i].begin(), g[i].end()}; //将set转vectortmp.insert(tmp.begin(), accounts[i][0]); //头插名字ans.push_back(tmp);}}return ans;}
};4、 839.相似字符串组🟡
如果交换字符串
X中的两个不同位置的字母,使得它和字符串Y相等,那么称X和Y两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。例如,
"tars"和"rats"是相似的 (交换0与2的位置);"rats"和"arts"也是相似的,但是"star"不与"tars","rats",或"arts"相似。总之,它们通过相似性形成了两个关联组:
{"tars", "rats", "arts"}和{"star"}。注意,"tars"和"arts"是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。给你一个字符串列表
strs。列表中的每个字符串都是strs中其它所有字符串的一个字母异位词。请问strs中有多少个相似字符串组?
解题思路:暴力遍历+dfs查询相似字符串,将相似字符串合并,最终返回集合个数
class Solution {
public:int numSimilarGroups(vector<string>& strs) {int n = strs.size();//初始化vector<int> fa(n);iota(fa.begin(), fa.end(), 0);//查询function<int(int)> find = [&](int x) -> int { return x == fa[x] ? x : fa[x] = find(fa[x]); }; int vis[n];memset(vis, 0, sizeof(vis));//dfsfunction<void(int)> is_same = [&](int i) -> void {vis[i] = true;string& s1 = strs[i];for (int j = 0; j < n; j++) {if (!vis[j]) {string& s2 = strs[j];if (s1 == s2) { //相同字符串相似,直接合并fa[find(j)] = fa[i];is_same(j);} else {int dif = 0;for (int k = 0; k < s1.size(); k++) {if (s1[k] != s2[k]) dif++;if (dif > 2) break;}if (dif == 2) { //恰有两个位置字符不同则相似,合并fa[find(j)] = fa[i];is_same(j);}}}}};//dfs入口for (int i = 0; i < n; i++) {if(!vis[i]) is_same(i);}//用set去重,返回集合个数set<int> ans;for (int i = 0; i < n; i++) ans.insert(find(i)); //将根节点插入set中return ans.size();}
};5、 2812.找出最安全路径 🔴
给你一个下标从 0 开始、大小为
n x n的二维矩阵grid,其中(r, c)表示:
- 如果
grid[r][c] = 1,则表示一个存在小偷的单元格- 如果
grid[r][c] = 0,则表示一个空单元格你最开始位于单元格
(0, 0)。在一步移动中,你可以移动到矩阵中的任一相邻单元格,包括存在小偷的单元格。矩阵中路径的 安全系数 定义为:从路径中任一单元格到矩阵中任一小偷所在单元格的 最小 曼哈顿距离。
返回所有通向单元格
(n - 1, n - 1)的路径中的 最大安全系数 。单元格
(r, c)的某个 相邻 单元格,是指在矩阵中存在的(r, c + 1)、(r, c - 1)、(r + 1, c)和(r - 1, c)之一。两个单元格
(a, b)和(x, y)之间的 曼哈顿距离 等于| a - x | + | b - y |,其中|val|表示val的绝对值。
解题思路:由题,求从左上角到右下角路径中的最小安全系数的最大值:倒序枚举答案(安全系数), 将>=当前安全系数的坐标用并查集相连(合并),一次循环结束判断左上角与右下角是否相连
class Solution {
public:static constexpr int dirs[5] = {1, 0, -1, 0, 1};int maximumSafenessFactor(vector<vector<int>>& grid) {int n = grid.size();vector<pair<int, int>> q;vector<vector<int>> dis(n, vector<int>(n, -1));for (int i = 0; i < n; i++) {for (int j = 0;j < n; j++) {if(grid[i][j] == 1) {q.push_back({i, j});dis[i][j] = 0;}}}//bfs求每个点安全系数,及不同安全系数的值的下标(用于后续并查集的合并)vector<vector<pair<int, int>>> groups = {q};while (!q.empty()) {int safe = groups.size();vector<pair<int, int>> tmp;for (auto &[i, j] : q) {for (int k = 0; k < 4; k++) {int x = i + dirs[k], y = j + dirs[k + 1];if (x >= 0 && x < n && y >= 0 && y < n && dis[x][y] < 0) {dis[x][y] = safe;tmp.push_back({x, y});}}}if (tmp.size() > 0)groups.push_back(tmp);q = move(tmp);}//初始化vector<int> fa(n*n);for (int i = 0; i < n * n; i++) fa[i] = i;//查询function<int(int)> find = [&](int x) -> int { return x == fa[x] ? x : fa[x] = find(fa[x]); };for (int ans = groups.size() - 1; ans > 0; ans--) {for (auto& [i, j] : groups[ans]) {for (int k = 0; k < 4; k++) {int x = i + dirs[k], y = j + dirs[k + 1];if (x >= 0 && x < n && y >= 0 && y < n && dis[x][y] >= dis[i][j]) fa[find(x * n + y)] = find(i * n + j); //合并}}if (find(0) == find((n - 1) * n + n - 1)) return ans; //相通则返回答案}return 0;}
};





![[Leetcode] [Tutorial] 多维动态规划](https://img-blog.csdnimg.cn/4e9a390120534b0286f50e517ad0aad8.png#pic_center)