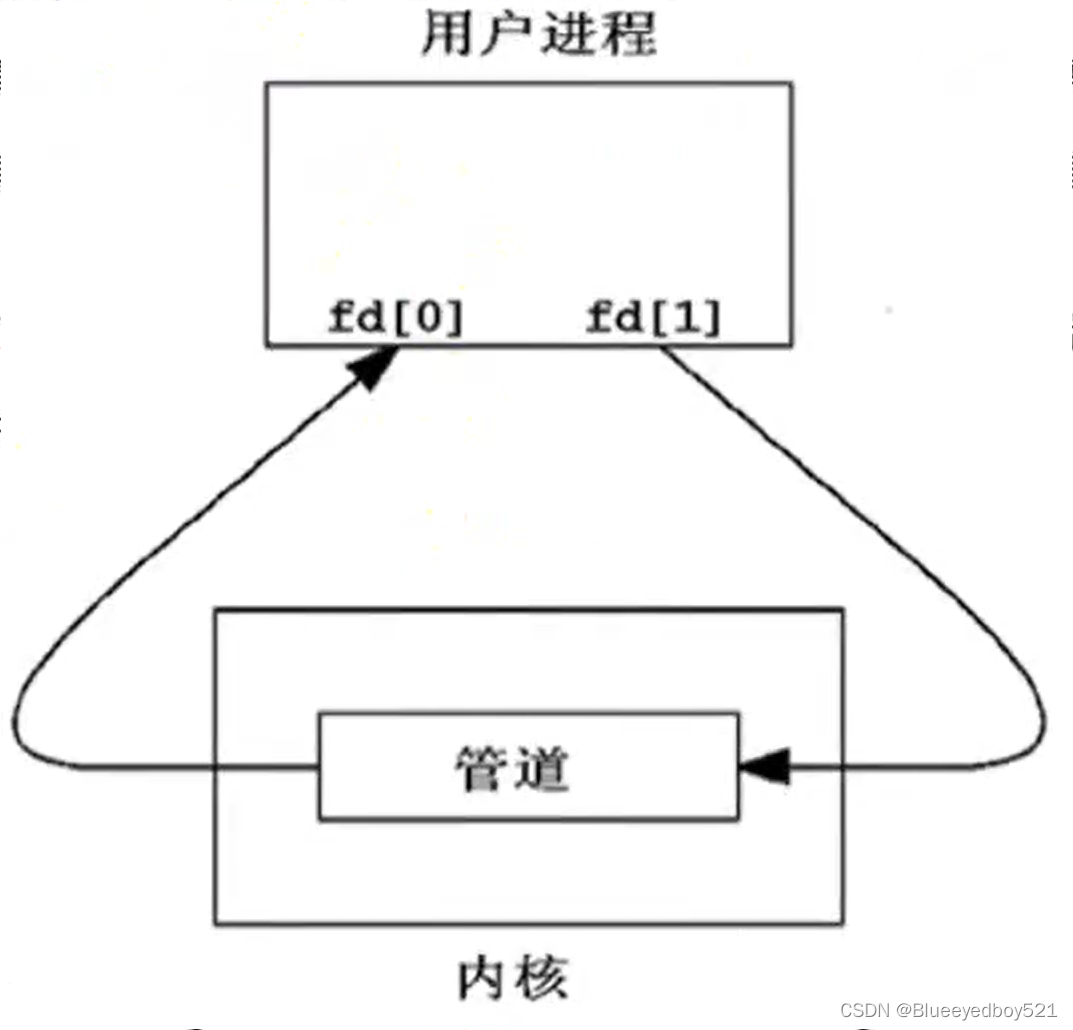
为了在最小功率损耗的情况下得到最大的加速电压，我们需要最大化分路阻抗（shunt impedance）。
由公式
$$R=\left(\frac{R}{Q}\right)Q$$
可知道，如果增加分路阻抗的大小，可以通过提高Q，或者提高R/Q来实现。

这里的Q指的是$Q_0$。
通常在超导腔的优化中，希望最大化$Q_0$。

这是因为由于超导腔材料的特性，在低温下的电阻通常非常小接近于0，超导腔能够在几乎不损耗能量的情况下实现很高品质的谐振。因此超导腔的阻抗并不是它的性能瓶颈，因此超导的优化目标通常是最大化$Q_0$。

为了得到特定加速电压下最小的储能，可以优化腔的形状来优化R/Q。

下面的腔型就是典型的优化了R/Q的例子：

鼻锥形状减少了加速间隙，提高了渡越因子，并且将电场集中到了束流的路径。

此外将磁场能量集中的趋于优化成了几乎为球形，已减少表面电流，缩短表面电路的路径。

对于上面的形状的腔和优化的pillbox腔的参数如下：

	re-entrant cavity	pillbox cavity
R/Q	111 Ω	107.5 Ω
Q	44270	41630
R	4.9 MΩ	4.47 MΩ

注：Pillbox腔的$R/Q$和$Q_0$的公式如下：
${\frac{R}{Q}}_{\text{pillbox}}=\frac{4\eta }{{\chi }_{01}^3\pi J_1^2({\chi }_{01})}\frac{{\sin }^2\left(\frac{{\chi }_{01}}{2}\frac{\ell }{a}\right)}{\frac{\ell }{a}}$
$Q_{0,\mathrm{pillbox}}=\frac{\sqrt{2a\eta \sigma {\chi }_{01}}}{2\left(1+\frac{a}{\ell }\right)}$

优化R/Q，通常出现在需要平衡储能和能量损耗的情况，即在合理的损耗之内获得最大的储能。

3.10 束流负载

从前面的等效电路可知道，束流吸收的功率为：
− 1 2 ℜ { V a c c I B ∗ } -\frac12\Re\{V_{\mathrm{acc}}I_{\mathrm{B}}^*\} −21​ℜ{Vacc​IB∗​}
之所以会出现负号，是因为按照惯例我们将从束流获取的感应电流对应的能量定义为正号。

束流负载会造成一些负面的影响：当优化的分路阻抗很高时，会因为束流负载效应而导致很高的束流感应电压。

从等效电路可以知道，束流看到的电阻是功率源内阻和分路阻抗的并联电阻：
$$R/(1+\beta )$$

当点电荷q，在0时刻经过一个初始状态的腔时（腔的能量为0），这个过程可以等效为给等效电路中的电容C充电的过程。
感应出的电压为q/C。
粒子的能量损失为：
$$\Delta W=\frac{q^2}{2C}$$
代入$C=\frac{Q_0}{R{\omega }_0}$，将粒子损失的能量与腔体的特性联系起来，有：
$$\Delta W=\frac{{\omega }_0}{2}\frac{R}{Q}{q}^2$$
令$k_{loss}=\frac{{\omega }_0}{2}\frac{R}{Q}$，可以得到：
$\Delta W\equiv k_{\text{loss}}{q}^2$
该式子表示将粒子经过腔时损失能量定义为一个常数$k_{loss}$与粒子电荷q的平方的乘积。

根据谐振电路的微分方程，可以得到带电粒子经过时，腔的电压变化的方程：
$$V(t)=\{\begin{array}{ll}0& \text{if}t<0\\ 2k_{\text{loss}}q{\text{e}}^{-\frac{{\omega }_0}{2Q_{\mathrm{L}}}t}\cos \left({\omega }_0\sqrt{1-\frac{1}{4Q_{\mathrm{L}}^2}}t\right)\text{if}t>0& \end{array}$$

这里的$Q_L=\frac{Q_0}{1+\beta }$。

其中$\frac{V_{\mathrm{acc}}}{2k_{\mathrm{loss}}q}$为归一化的振幅。

由$\frac{R}{Q}=\frac{|V_{\mathrm{acc}}{|}^2}{2{\omega }_{0}W}$和$k_{loss}=\frac{{\omega }_0}{2}\frac{R}{Q}$可以得到：

$k_{\mathrm{loss}}=\frac{|V_{\mathrm{acc}}{|}^2}{4W}=\frac{{\omega }_0}{2}\frac{R}{Q}$

看起来可能令人惊讶的是，损耗因子包含了$\frac{R}{Q}$，而没有分路阻抗。

换句话说：腔体中单个电荷损失的能量不取决于Q，而只取决于腔体的几何形状，这可以解释如下：一个经过的点电荷的能量损失在振荡的时间尺度上发生得很快——当腔体的Q开始起作用时，电荷已经不在了。当然这个推论仅仅限制为第一个粒子经过的能量为0的腔的情况。

下面我们来讨论瞬态束流负载的情况。

假如是同步储存环的情况，高频腔看到的束流是脉冲形式的，即高频腔可以看到暂态变换的束流感应电流$I_B$。由加速器纵向束流动力学可知道，粒子是在RF射频电压的过零点进入（自动稳相原理）。

也就是说感应的电流与RF加速电压的相位相差90°。

即等效电路中的$I_B$与$V_{acc}$相位相差90°。
因此位于过零点即同步相位的粒子的束流负载可以看作是纯感性的。

如果粒子的动量过大或者过小，则它会延时或者超前到达加速间隙，因此这些动量过大的粒子造成的束流感应电流的相位与加速电压相比将不再等于90°，而是大于或者小于90°。

因此束流造成的束流负载不再是一个纯电感，而是一个感抗。

因此为了补偿束流负载效应，应该让腔工作在略微容性的状态。
根据等效电路，如果功率源的频率小于谐振频率，则电路的等效阻抗为容性。
也就是说腔应该工作在比谐振频率略小的频率上。

量化的计算这个频率差为：
$-\Delta \equiv \frac{{\omega }_0-\omega }{{\omega }_0}=-\frac{1}{2}\left(\frac{R}{Q}\right)\frac{|I_{\mathrm{B}}|}{V_{\mathrm{acc}}}$

但是工作在较低的频率上又会造成加速效率的降低。

由上面的公式可以看出，在束流负载一定的情况下，比较小的R/Q值，会缓解这个问题。

可以通过优化算法优化设计腔的调谐频率和工作频率，以及通过快速束流负载反馈和前馈控制等方式解决束流负载问题。

说一下尾场效应：
根据之前的带电粒子经过时的腔压变化图，可知道前一个粒子经过后，会留下一个场，而这个场会对后面经过一段时间后到达的粒子产生作用，我们用尾场电势来表示这种作用。
之前的这个公式：
$V(t)=\{\begin{array}{cc}0& \text{if}t<0\\ 2k_{\text{loss}}q{\text{e}}^{-\frac{{\omega }_0}{2Q_{\text{L}}}t}\cos \left({\omega }_0\sqrt{1-\frac{1}{4Q_{\text{L}}^2}}t\right)\text{if}t>0& \end{array}$
也称为尾场方程。

然而，这只是其中的一种模式，而在实际的情况中，束流会激发很多的模式，而尾场方程也是各种模式下的尾场方程的叠加。

传递给束流的功率定义为：
P b e a m = − 1 2 ℜ { V a c c I B ∗ } P_{\mathrm{beam}}=-\frac{1}{2}\Re\{V_{\mathrm{acc}}I_{\mathrm{B}}^{*}\} Pbeam​=−21​ℜ{Vacc​IB∗​}
腔的功率损耗为：
$P=\frac{|V_{\mathrm{acc}}{|}^2}{2R}$

定义$\eta =\frac{P_{\mathrm{beam}}}{P+P_{\mathrm{beam}}}$为RF到束流的效率。

因此从上面的公式可以看出，在保证加速电压的情况下，为了提高RF到束流的效率唯一的办法就是增加分路阻抗，由$R=R/Q\ast Q$，因为R/Q有一个物理极限，因此只能通过进一步增加Q实现（例如采用超导腔，或使用多加速间隙的加速结构）。