前言

相信通过本模块的第一篇博客，大家已经能够对二分有一个清晰的认知了，最好画画图来加深理解，以下是一些新的注意事项：

1. 请⼤家⼀定不要觉得背下模板就能解决所有⼆分问题。⼆分问题最重要的就是要分析题意，然后确定要搜索的区间，根据分析问题来写出⼆分查找算法的代码。要分析题意，确定搜索区间，不要死记模板，不要看左闭右开什么乱七⼋糟的题解。要分析题意，确定搜索区间，不要死记模板，不要看左闭右开什么乱七⼋糟的题解。要分析题意，确定搜索区间，不要死记模板，不要看左闭右开什么乱七⼋糟的题解。重要的事情说三遍。
2. 模板记忆技巧：关于什么时候⽤三段式，还是⼆段式中的某⼀个，⼀定不要强⾏去⽤，⽽是通过具体的问题分析情况，根据查找区间的变化确定指针的转移过程，从⽽选择⼀个模板。
3. 当选择两段式的模板时：在求 mid 的时候，只有 right = mid - 1 的情况下，才会向上取整（也就是 +1 取中间数）。

题目描述

题目链接：34.在排序数组中查找元素的第一个和最后一个位置

非递减顺序说明是递增或者不变的，根据这个特性说明这道题具有二段性，且题目已经要求是O(log n)的时间复杂度，那就可以确定是二分了。

算法原理

接下来我将用x表示一个数，resLeft表示结果左边界，resRight表示结果右边界：

1. 左区间[left,resLeft - 1]都是小于x的，右区间[resLeft,right]都是大于等于x的；
2. 因此关于mid的落点，我们可以分两种情况讨论：
   
   
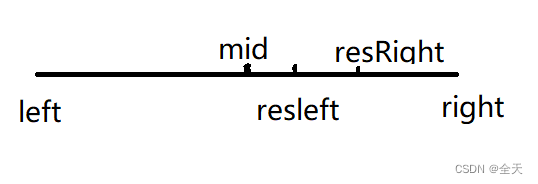
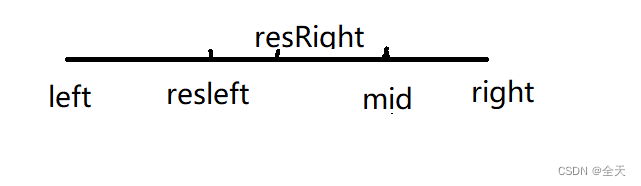
   情况一：nums[mid] < target，舍去左区间，left更新到mid + 1；
   情况二：nums[mid] >= target，舍去右区间，right更新到mid。（中点向下取整）
3. 上述分析为寻找左边界的过程，其实就是使用了我们寻找左边界的模板，接着再根据题意使用寻找右边界的模板即可，忘了的同学可以再去看看，还是牢记一件事：分析题意，确定搜索区间，不要死记模板。
4. 左区间[left,resRight]都是小于等于x，右区间[resRight + 1,right]都是大于x；
5. 分析mid：情况一：mid在左区间，left = mid；情况二：mid在右区间，right = mid - 1。（中点向上取整）

细节问题

结束条件应该为left < right，left = right的时候就是结果，判断就会死循环。
寻找右边界后续移动左右指针的时候：
左指针：left = mid ，可能会原地踏步（⽐如：如果向下取整的话，如果剩下 1，2 两个元素，left == 1，right == 2，mid == 1。更新区间之后， left，right，mid的值没有改变，就会陷⼊死循环）；
右指针： right = mid - 1 ，是会向前移动的，因此区间是会缩⼩的；

因此⼀定要注意，当 right = mid - 1的时候，要向上取整，寻找左边界同理可分析。

代码实现

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {//根据二段性可以使用二分int left = 0,right = nums.size() - 1;//记录结果int begin = 0,end = 0;//单独处理空数组if(nums.empty())return {-1,-1};//查找左端点while(left < right){int mid = left + (right - left) / 2;if(nums[mid] >= target){right = mid;}else if(nums[mid] < target){left = mid + 1;}}begin = (nums[left] == target) ? left : -1;left = 0,right = nums.size() - 1;//查找右端点while(left < right){int mid = left + (right - left + 1) / 2;if(nums[mid] <= target){left = mid;}else if(nums[mid] > target){right = mid - 1;}}end = (nums[left] == target) ? left : -1;return {begin,end};}
};