E. Rudolf and k Bridges
题意不讲了,不如去题干看图。
传统dp,每个点有两个选择,那么建桥要么不建。需要注意的是在状态转移的时候,桥是有长度的,如果不建需要前d格中建桥花费最少的位置作为状态转移的初态。
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <unordered_set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 2e5+5;struct contianer {private:int step;int pos = 0;ll loop[maxn];multiset<ll> store;public:contianer(int step):step(step) {}void add(ll x) {int now = pos % step;// need to removeif (pos >= step) {store.erase(store.find(loop[now]));}loop[now] = x;store.insert(x);pos ++;}/*** get min number*/ll get() {return *store.begin();}void setStep(int s);void clear();
};void contianer::setStep(int s) {step = s;
}void contianer::clear() {store.clear();pos = 0;
}ll sum[128];
int store[maxn];
ll dp[maxn][2];
int main() {IOSint t;cin>>t;while(t--) {int n,m,k,d;cin>>n>>m>>k>>d;contianer heap(d);sum[0] = 0LL;// input and dprep(_,0,n) {// inputrep(i,0,m) cin>>store[i];// initheap.clear();heap.add(store[0] + 1);dp[0][0] = dp[0][1] = store[0] + 1;// dprep(i,1,m-1) {ll min_cost = heap.get();dp[i][0] = min_cost;dp[i][1] = min(dp[i-1][0], min_cost) + store[i] + 1;
// cout<<"dp["<<i<<"][0]:"<<dp[i][0]<<" dp["<<i<<"][1]:"<<dp[i][1]<<endl;heap.add(dp[i][1]);}// costsum[_ + 1] = min(dp[m-2][1], dp[m-2][0]) + 1LL;
// cout<<sum[_+1]<<endl;}// pre sumrep(i,1,n+1) sum[i] += sum[i-1];// the k minll ans = sum[k] - sum[0];rep(i,k+1,n+1) {ans = min(ans, sum[i] - sum[i-k]);}// coutcout<<ans<<endl;}return 0;
}
F. Rudolf and Imbalance
求两数和的plus版本。给出数组a,现在要分别从d和f挑选一个数相加后放入a,使得所有 a i + 1 − a i a_{i+1} - a_i ai+1−ai中最大值尽可能小。
显然,我们只要找到在没有挑选插入前 a i + 1 − a i a_{i+1} - a_i ai+1−ai的最大值以及 i i i的值,然后构造 a i + 1 > d + f > a i a_{i+1} > d+f > a_i ai+1>d+f>ai,就可以破坏最大值。且 d + f = a i + 1 + a i 2 d+f = \frac {a_{i+1} + a_i}{2} d+f=2ai+1+ai时,能将最大值分割的尽可能小。
其中,如果最大值和第二大值一样,那么无论怎么分割都改变不了最大值,可以直接输出。
至于怎么让 d + f d+f d+f尽可能靠近中点就不细说了,固定d然后二分搜索f。这里我脑干缺失写了个int target = abs(aim - commonA);我是真的睿智
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 2e5+5;struct record{int val;int ind;
};int store[maxn/2];
record dif[maxn/2];
int d[maxn], f[maxn];
bool cmp(const record& a, const record& b) {return a.val < b.val;
}
int abs(int a) {if (a<0) return -a;else return a;
}
int main() {IOSint t;cin>>t;while(t--) {int n,m,k;cin>>n>>m>>k;int pos = 0;cin>>store[0];rep(i,1,n) {cin>>store[i];dif[pos].ind = i;dif[pos ++].val = store[i] - store[i-1];}sort(dif, dif+pos,cmp);
// rep(i,0,pos) cout<<dif[i].val<<endl;int len_d , len_f;if (m < k) {rep(i,0,m) cin>>d[i];sort(d, d+m);len_d = m;rep(i,0,k) cin>>f[i];sort(f, f+k);len_f = k;} else {rep(i,0,m) cin>>f[i];sort(f,f+m);len_f = m;rep(i,0,k) cin>>d[i];sort(d,d+k);len_d = k;}if (pos > 2 && dif[pos-1].val == dif[pos-2].val) {cout<<dif[pos-1].val<<endl;continue;}int sup = store[dif[pos-1].ind];int inf = store[dif[pos-1].ind - 1];int aim = inf + (sup - inf)/2;int minn = dif[pos-1].val;rep(i,0,len_d) {int commonA = d[i];if (commonA >= sup) break;int target = aim - commonA;
// cout<<"d[i]:"<<d[i]<<" target:"<<target<<endl;auto it = upper_bound(f, f+len_f-1, target);
// cout<<"it:"<<it<<endl;int commonB = *it;
// cout<<"find:"<<commonB<<endl;int num = commonA + commonB;if (inf<num && num<sup)minn = min(minn, max(sup - num ,num - inf));if (it != f) {commonB = *(it-1);num = commonA + commonB;if (inf<num && num<sup)minn = min(minn, max(sup - num ,num - inf));}}/*if (d[0] + f[0] < store[0]) {aim = store[0];rep(i,0,len_d) {int commonA = d[i];if (commonA >= aim) break;int target = abs(aim - commonA);auto it = lower_bound(f, f+len_f-1, target-1);int commonB = *it;cout<<"commonA:"<<commonA<<" commonB:"<<commonB<<" target:"<<target<<endl;int num = commonA + commonB;if (num < store[0])minn = min(minn, store[0] - num);if (it != f) {commonB = *(it-1);num = commonA + commonB;if (num < store[0])minn = min(minn, store[0] - num);}}}aim = store[n-1];if (d[len_d-1] + f[len_f-1] > aim)rep(i,0,len_d) {int commonA = d[i];int target = abs(aim - commonA);auto it = upper_bound(f, f+len_f-1, target+1);int commonB = *it;int num = commonA + commonB;if (num > aim) {minn = min(minn, num - aim);}if(it == f) break;}*/cout<<max(minn, pos>=2? dif[pos-2].val : 0)<<endl;}return 0;
}
G. Rudolf and Subway
很好的图论使我小脑萎缩
边染色,求A->B最少经过几种颜色。其中相同颜色的边一定构成连通图。
机智如我并没有按照题解中加边的思路,而是采用合并点的方式,从颜色的维度处理。将相同颜色的边视为从同一个点出发(因为相同颜色内移动不会影响结果,只有移动到新的颜色上才会影响结果),从而将问题转化为最短路。采用bfs那么首先经过的颜色一定是最短路,从而可以作为优化的条件。
此外由于是边染色,所有可能一个点会被多个颜色所合并。如果在颜色A的合并点里走到了点v,同时v又连接B、C等颜色的边,虽然后续B、C颜色的合并也会重新遍历v的边,但是由于bfs的特性此时的遍历不会影响已经过的颜色A,也不会加入新的颜色(因为v涉及的所有颜色都在颜色A的合并点中加入到了队列),所以图中的每个点只需要访问一次,不需要重复访问。
没有这个优化会T 嘤嘤嘤
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 2e5+5;struct node{int to;int color;
};queue<int> Q;
bool vis[maxn],visNode[maxn];
int dis[maxn];
set<int> colors;
set<int> colorSet[maxn];
vector<node> adj[maxn];
int main() {IOScout.tie(0);int t;cin>>t;while(t--) {for(auto it=colors.begin();it!=colors.end();it++){vis[*it] = false;colorSet[*it].clear();}colors.clear();int n,m;cin>>n>>m;rep(i,0,n+1) {adj[i].clear();visNode[i] = false;}rep(i,0,m) {int commonA,commonB,color;cin>>commonA>>commonB>>color;adj[commonA].push_back({commonB, color});adj[commonB].push_back({commonA, color});colorSet[color].insert(commonA);colorSet[color].insert(commonB);colors.insert(color);}int commonA,commonB;cin>>commonA>>commonB;if (commonA==commonB) {cout<<0<<endl;continue;}for(auto it=colors.begin();it!=colors.end();it++)dis[*it] = INT_MAX;visNode[commonA] = true;rep(i,0,adj[commonA].size()) {node edge = adj[commonA][i];if (!vis[edge.color]) {Q.push(edge.color);
// cout<<"push color:"<<edge.color<<endl;dis[edge.color] = 1;vis[edge.color] = true;}}while(!Q.empty()) {int now = Q.front();
// cout<<"color:"<<now<<" dis:"<<dis[now]<<endl;Q.pop();for(int v : colorSet[now]) {if (visNode[v]) continue;visNode[v] = true;int len = adj[v].size();rep(i,0,len) {node next = adj[v][i];int next_color = next.color;if (vis[next_color] || visNode[next.to]) continue;dis[next_color] = dis[now]+1;Q.push(next_color);vis[next_color] = true;}}}int ans = INT_MAX;rep(i,0,adj[commonB].size()) {node edge =adj[commonB][i];int des_color = edge.color;ans = min(ans, dis[des_color]);}cout<<ans<<endl;}return 0;
}
官方题解则是通过加边的方法传送门
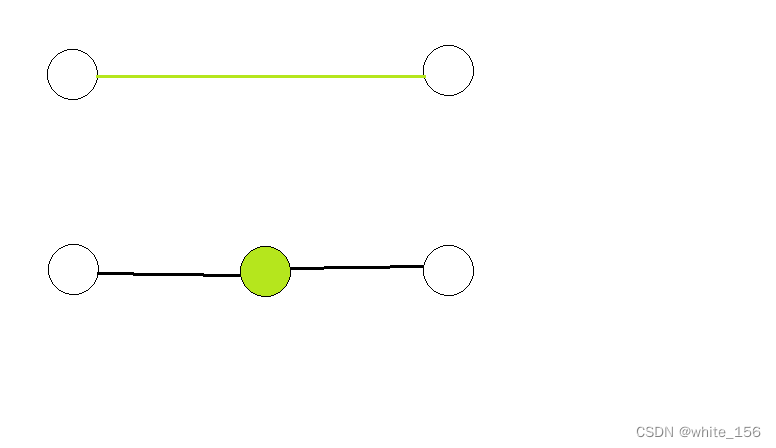 将染色边转化为一个新的染色节点连接到原有边的端点。可能这样画体现不出这个方法精妙之处。
将染色边转化为一个新的染色节点连接到原有边的端点。可能这样画体现不出这个方法精妙之处。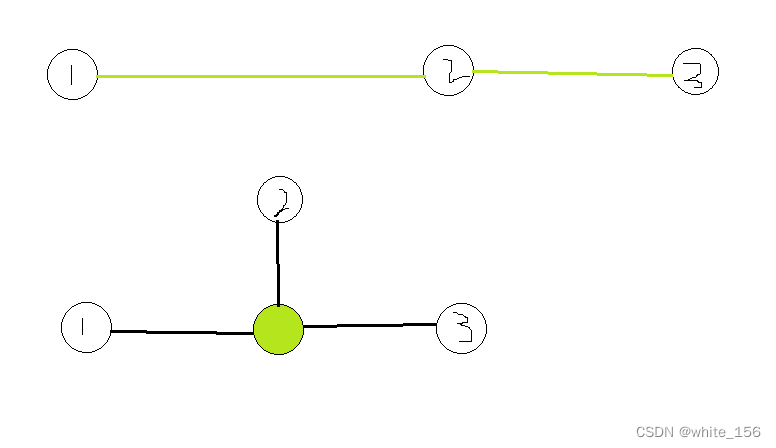 点多了就能看出来,这样形成一个星形的连接,相同颜色的点之间移动都只需要经过两条边。仍然还是bfs,只不过由于边多加了,所以需要最终结果/2
点多了就能看出来,这样形成一个星形的连接,相同颜色的点之间移动都只需要经过两条边。仍然还是bfs,只不过由于边多加了,所以需要最终结果/2