【数据结构】二叉树（定义、性质、存储、遍历、构造）解析+完整代码-编程知识

文章目录

- 1.树的基本概念
- 2.二叉树的概念
- - 2.1 二叉树定义和特性
  - 2.2 二叉树性质
  - 2.3 二叉树的存储
  - - 2.3.1 顺序存储
    - 2.3.2 链式存储
- 3.二叉树的遍历
- - 3.1 先序遍历
  - 3.2 中序遍历
  - 3.3 后序遍历
  - 3.4 层序遍历
  - 3.5 由遍历序列构造二叉树
  - - A.前序+中序遍历序列
    - B.后序+中序遍历序列
    - C.层序+中序遍历序列
- *完整代码二叉树

1.树的基本概念

定义
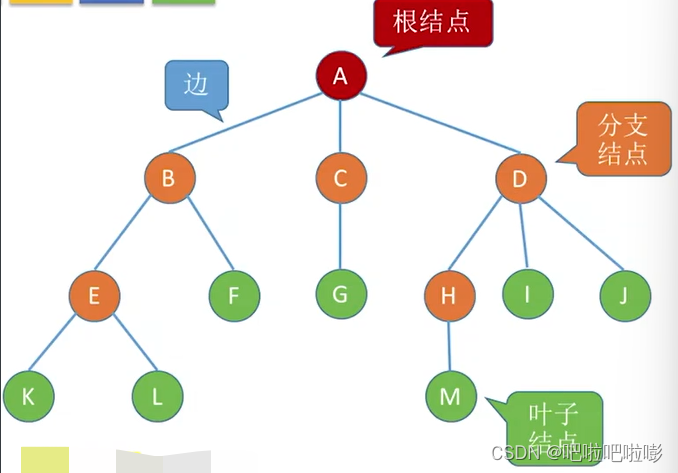
- 空树：结点数为0的树
- 非空树：有且仅有一个根结点
- 叶子结点：没有后继的结点（终端结点）
- 分支节点：有后继的结点（非终端结点）
- 根节点没有前驱，其他任何一个结点都有且仅有一个前驱
基本术语
- 1.度
  
  结点的度：树中一个结点的孩子个数。
  
  树的度：树中结点的最大度数。
- 2.结点的深度（层次）
  
  从上往下数，在第几层。
- 3.结点的高度
  
  从下往上数，在第几层。
- 4.树的高度（深度）
  
  总共多少层。
- 5.有序树和无序树
  
  有序树：树中各子树从左至右是有次序的，不能互换。
  
  无序树：子树无次序，可以互换。
- 6.森林
  
  森林是m棵互不相交的树的集合
树的性质
- 1.结点数=总度数+1
  
  度数即孩子的个数，加一的那个为根结点
- 2.度为m的树、m叉树的区别
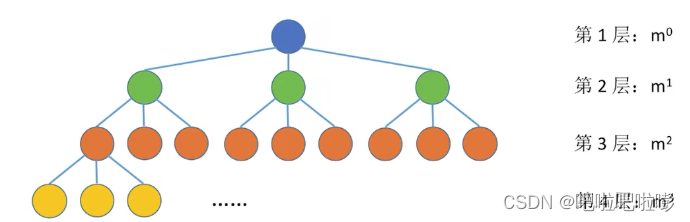
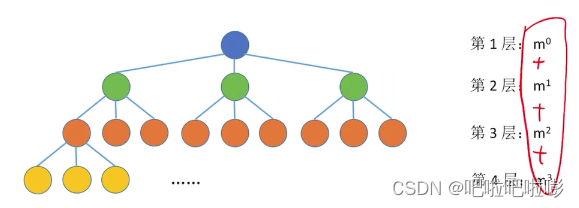
- 3.度为m的树第i层至多有 $m^{i-1}$ 个结点
  
  m叉树第i层至多有 $m^{i-1}$ 个结点
- 4.高度为h的m叉树至多有 $\frac{m^h-1}{m-1}$ 个结点
- 5.高度为h的m叉树至少有h个结点
  
  高度为h、度为m的树至少有h+m-1个结点
- 6.具有n个结点的m叉树的最小高度为 $\lceil log_m(n(m-1)+1) \rceil$
  
  根据不等式求解：

2.二叉树的概念

2.1 二叉树定义和特性

定义

1.每个结点至多有两棵子树；

2.左右子树不能颠倒（二叉树是有序树）。
特殊二叉树
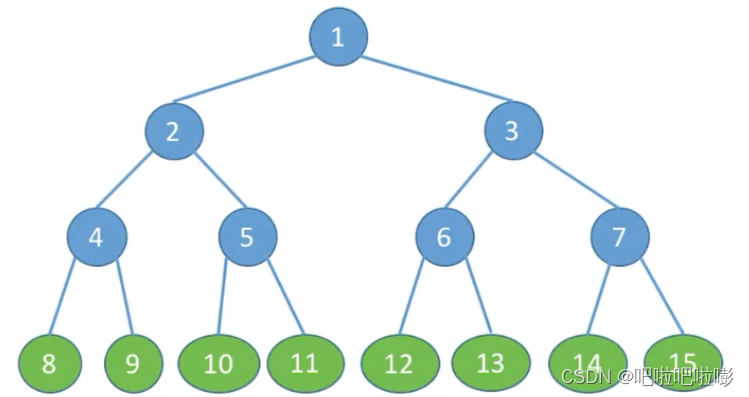
- 1.满二叉树
  
  一棵高度为h，且含有 $2^h-1$ 个结点的二叉树。
  
  特点：
  
  （1）只有最后一层有叶子结点；
  
  （2）不存在度为1的结点；
  
  （3）按层序从1开始编号，结点i的左孩子为 $2 i$ ，右孩子为 $2 i + 1$ ；结点i的父节点为 $\lfloor i/2 \rfloor$ 。
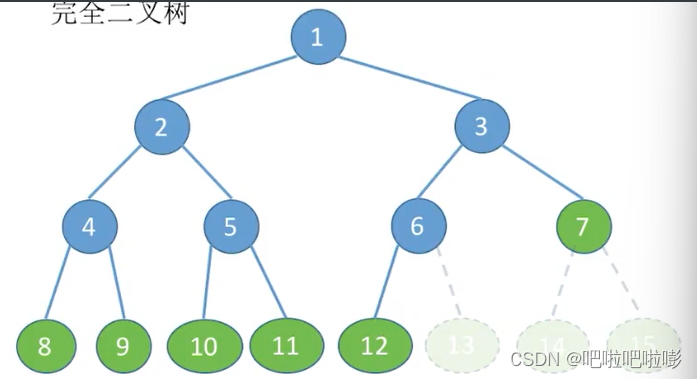
- 2.完全二叉树
  
  当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时，称为完全二叉树。
  
  即在满二叉树的基础上，最后一层可以不满。
  
  特点：
  
  （1）只有最后两层可能有叶子结点；
  
  （2）最多只有一个度为1的结点；
  
  （3）和满二叉树相同：按层序从1开始编号，结点i的左孩子为 $2 i$ ，右孩子为 $2 i + 1$ ；结点i的父节点为 $\lfloor i/2 \rfloor$ 。
  
  （4） $i<\lfloor n/2 \rfloor$ 为分支结点， $i>\lfloor n/2 \rfloor$ 为叶子结点。
  
  （5）如果一个结点只有一个孩子，那一定是左孩子不是右孩子。
- 3.二叉排列树
  
  若一棵二叉树满足：左子树的元素<根节点<右子树
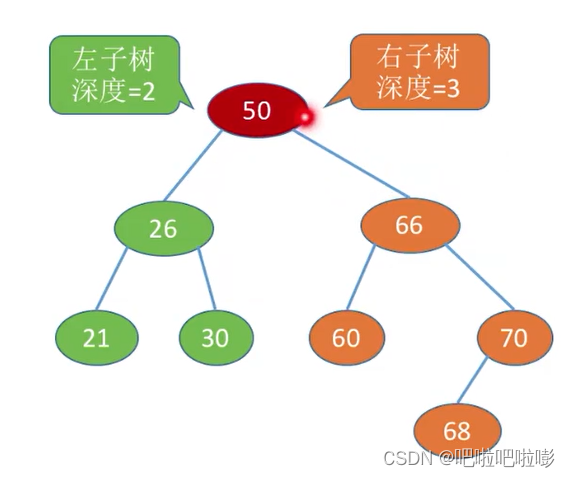
- 4.平衡二叉树
  
  树上任一结点的左子树和右子树的深度之差不超过1。

2.2 二叉树性质

1.设非空二叉树中度为0，1，2的结点个数分别为 $n_0、n_1、n_2$ ，则 $n_0=n_2+1$ 。（叶子结点比二分支结点多一个）

推导：
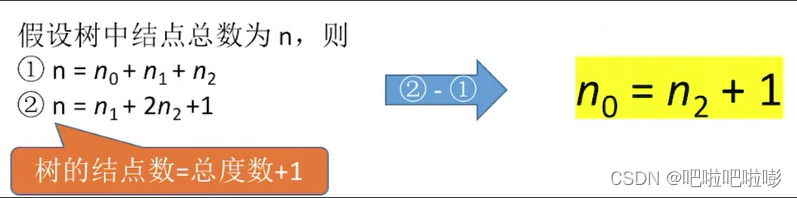
2.二叉树第i层至多有 $2^{i-1}$ 个结点

（m叉树第i层至多有 $m^{i-1}$ 个结点）
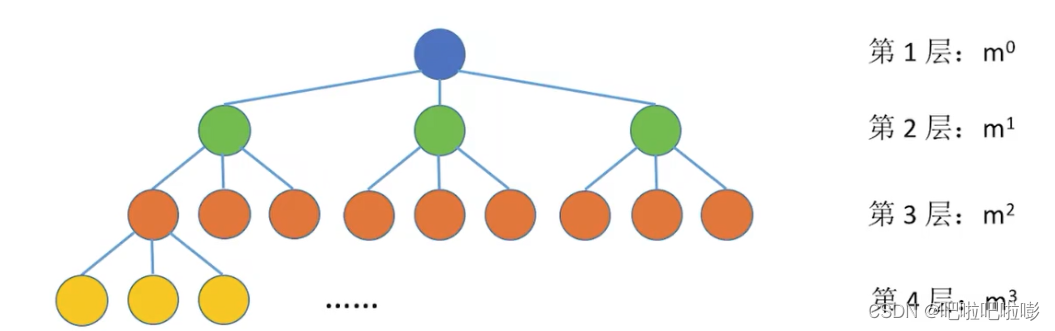
3.高度为h的二叉树至多有 $2^h-1$ 个结点（满二叉树）
4.对于完全二叉树，具有n个结点的完全二叉树的高度h为 $\lceil log_2(n+1) \rceil$ 或 $\lfloor log_2n \rfloor+1$

推导：
5.对于完全二叉树，可以由结点数n推出度为0，1，2的结点个数为 $n_0、n_1、n_2$ ，完全二叉树最多只有一个度为1的结点，即

$n_1=0或1$

$n_0=n_2+1$ —> $n_0+n_2$ 一定是奇数

====》

若完全二叉树有2k个（偶数）个结点，则必有 $n_1=1,n_0=k,n_2=k-1$

若完全二叉树有2k-1个（奇数）个结点，则必有 $n_1=0,n_0=k,n_2=k-1$

2.3 二叉树的存储

2.3.1 顺序存储

结构体

struct TreeNode{ElemType value; //结点中的数据元素bool isEmpty; //结点是否为空
};

用数组定义，按从上至下（一层层）、从左至右的顺序依次存储完全二叉树中各个结点
```
TreeNode t[MaxSize];
```

初始化时标记所有结点为空

for(int i=0;i<MaxSize;i++){t[i].isEmpty=true;
}

完全二叉树顺序存储后的几个基本操作
- i的左孩子 —— $2 i$
- i的右孩子 —— $2 i + 1$
- i的父节点 —— $\lfloor i/2 \rfloor$
- i所在层次 —— $\lceil log_2(n+1) \rceil$ 或 $\lfloor log_2n \rfloor+1$
若完全二叉树中共有n个结点，则
- 判断i是否有左孩子？
  
  $2 i <= n$
- 判断i是否有右孩子？
  
  $2 i + 1 <= n$
- 判断i是否是叶子/分支结点？
  
  $\lfloor n/2 \rfloor$
非完全二叉树中，，把二叉树的结点编号与完全二叉树的对应起来：
- 这种存储方式会浪费很多空间。
- 最坏情况：高度为h且只有h个结点的单支树（所有结点只有右孩子），也至少需要 $2^h-1$ 个存储单元。
∴ 二叉树的顺序存储只适合存储完全二叉树。

2.3.2 链式存储

结构体

typedef struct BiTNode{ElemType data;struct BiTNode *lchild,*rchild; //每个结点都有左右两个孩子的指针struct BiTNode *parent; //可不加父指针
}BiTNode,*BiTree;

注：n个结点的二叉链表共有n+1个空链域：

3.二叉树的遍历

遍历：按照某种次序把所有结点都访问一次。
分类

先序遍历：根左右（NLR）

中序遍历：左根右（LNR）

后序遍历：左右根（LRN）
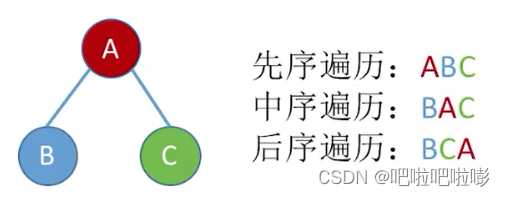
手算方法：分支节点逐层展开法
复杂度
- 时间复杂度：
  
  ∵ 每个结点都访问一次且只访问一次，
  
  ∴ 时间复杂度 $O (n)$ 。
- 空间复杂度：
  
  ∵ 最坏情况下，二叉树是有n个结点且深度为n的单支树，计算机中递归实现用栈存储，
  
  ∴ 空间复杂度为 $O (n)$ 。

3.1 先序遍历

先序遍历过程：根左右（NLR）

1.若二叉树为空，什么都不做；

2.若二叉树非空：

（1）访问根结点；

（2）先序遍历左子树；

（3）先序遍历右子树。

typedef struct BiTNode{ElemType data;struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;void PreOrder(BiTree T){if(T!=NULL){visit(T); //访问根结点PreOder(T->lchild); //递归遍历左子树PreOrder(T->rchild); //递归遍历右子树}
}

3.2 中序遍历

中序遍历过程：左根右（LNR）

1.若二叉树为空，什么都不做；

2.若二叉树非空：

（1）先序遍历左子树；

（2）访问根结点；

（3）先序遍历右子树。

typedef struct BiTNode{ElemType data;struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;void InOrder(BiTree T){if(T!=NULL){PreOder(T->lchild); //递归遍历左子树visit(T); //访问根结点PreOrder(T->rchild); //递归遍历右子树}
}

3.3 后序遍历

后序遍历过程：左右根（LRN）

1.若二叉树为空，什么都不做；

2.若二叉树非空：

（1）先序遍历左子树；

（2）先序遍历右子树。

（3）访问根结点。

typedef struct BiTNode{ElemType data;struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;void PostOrder(BiTree T){if(T!=NULL){PreOder(T->lchild); //递归遍历左子树PreOrder(T->rchild); //递归遍历右子树visit(T); //访问根结点}
}

3.4 层序遍历

算法思想
- 层序遍历就是从上往下一层一层访问
1.初始化一个辅助队列；

2.根结点入队；

3.若队列非空，则队头结点出队，访问该节点，并将其左右孩子插入队尾；

4.重复第三次直到队列空。

void LevelOrder(BiTree T){LinkQueue Q;InitQueue(Q);BiTree p;EnQueue(Q,T); //将根结点入队while(!IsEmpty(Q)){ //队列不空则循环DeQueue(Q,p); //队头结点出队visit(p); //访问出队结点if(p->lchild!=NULL)EnQueue(Q,p->lchild); //左孩子入队if(p->rchild!=NULL)EnQueue(Q,p->rchild); //右孩子入队}
}

补充代码：链式队列结点

typedef struct LinkNode{BiTNode *data;struct LinkNode *next;
}LinkNode;typedef struct{LinkNode *front,*rear; //队头队尾指针
}LinkQueue;

3.5 由遍历序列构造二叉树

若只给出一棵二叉树的前中后层序遍历中的一种，不能唯一确定一棵二叉树。
- 构造的三种方法：
  1. 前序+中序
  2. 后序＋中序
  3. 层序+中序

A.前序+中序遍历序列

步骤

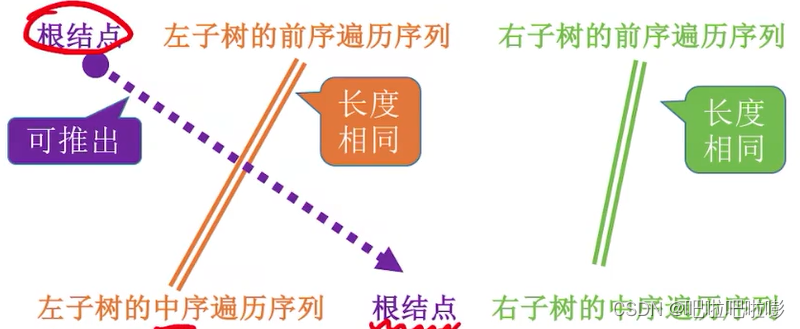
1.找到根结点：先序序列第一个结点==根节点；

2.在中序序列中找到根结点，根据根结点把序列分成：左子树+根结点+右子树；

3.左右子树分别重复第1、2步。
方法：根据根结点推，前序遍历序列的第一个就是根节点。

B.后序+中序遍历序列

方法：根据根结点推，后序遍历序列的最后一个一个就是根结点。

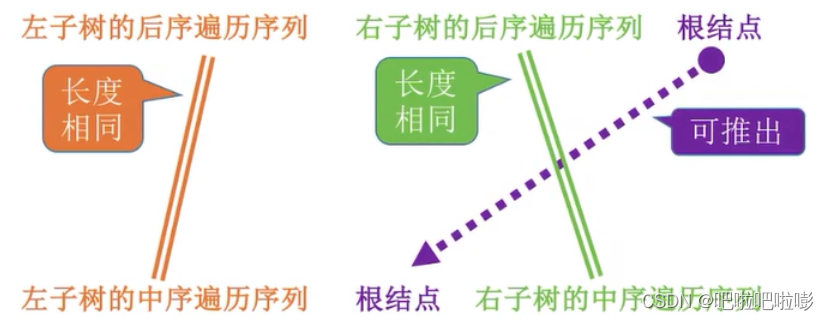
C.层序+中序遍历序列

方法：

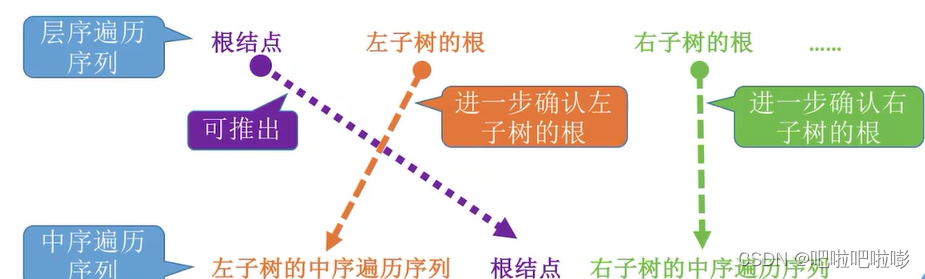
*完整代码二叉树

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>#define ElemType int// 二叉树链式存储结构
typedef struct BiTNode {ElemType data; // 数据域struct BiTNode *lchild, *rchild; // 左右孩子指针
} BiTNode, *BiTree;// 访问结点
void visit(BiTNode *Node) {printf("%d ", Node->data);
}// 先序遍历：根左右
void PreOrder(BiTree T) {if (T != NULL) {visit(T); // 访问根结点PreOrder(T->lchild);PreOrder(T->rchild);}
}// 中序遍历：左根右
void InOrder(BiTree T) {if (T != NULL) {InOrder(T->lchild);visit(T);InOrder(T->rchild);}
}// 后序遍历：左右根
void PostOrder(BiTree T) {if (T != NULL) {PostOrder(T->lchild);PostOrder(T->rchild);visit(T);}
}// 层序遍历：借助队列
// 链式队列结点
typedef struct LinkNode {BiTNode *data;struct LinkNode *next;
} LinkNode;typedef struct {LinkNode *front, *rear;
} LinkQueue;void InitQueue(LinkQueue *Q) {Q->front = Q->rear = (LinkNode *)malloc(sizeof(LinkNode));Q->front->next = NULL; // 将头节点的 next 指针初始化为 NULL
}void Push(LinkQueue *Q, BiTNode *x) {LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));p->data = x;p->next = NULL;Q->rear->next = p;Q->rear = p;
}void Pop(LinkQueue *Q, BiTNode **x) {LinkNode *p = Q->front->next;*x = p->data;Q->front->next = p->next;if (Q->rear == p) Q->rear = Q->front;free(p);
}bool Empty(LinkQueue *Q) { // 修改函数参数if (Q->rear == Q->front)return true;elsereturn false;
}void LevelOrder(BiTree T) {LinkQueue Q;InitQueue(&Q);BiTree p;Push(&Q, T); // 根结点入队while (!Empty(&Q)) {Pop(&Q, &p); // 队头结点出队visit(p);// 若左孩子不为空，则入队if (p->lchild != NULL) {Push(&Q, p->lchild);}// 若右孩子不为空，则入队if (p->rchild != NULL) {Push(&Q, p->rchild);}}
}// 中序加先序遍历构造二叉树
BiTree InPreCreateBiTree(ElemType in[], ElemType pre[], int inStart, int inEnd, int preStart, int preEnd) {if (inStart > inEnd || preStart > preEnd) return NULL;BiTree root = (BiTNode *)malloc(sizeof(BiTNode));root->data = pre[preStart]; // 根节点为先序遍历的第一个节点int rootIndex;for (rootIndex = inStart; rootIndex <= inEnd; rootIndex++) {if (in[rootIndex] == pre[preStart]) // 在中序遍历中找到根节点位置break;}int leftLength = rootIndex - inStart; // 左子树长度root->lchild = InPreCreateBiTree(in, pre, inStart, rootIndex - 1, preStart + 1, preStart + leftLength); // 递归构造左子树root->rchild = InPreCreateBiTree(in, pre, rootIndex + 1, inEnd, preStart + leftLength + 1, preEnd); // 递归构造右子树return root;
}// 中序加后序遍历构造二叉树
BiTree InPostCreateBiTree(ElemType in[], ElemType post[], int inStart, int inEnd, int postStart, int postEnd) {if (inStart > inEnd || postStart > postEnd) return NULL;BiTree root = (BiTNode *)malloc(sizeof(BiTNode));root->data = post[postEnd]; // 根节点为后序遍历的最后一个节点int rootIndex;for (rootIndex = inStart; rootIndex <= inEnd; rootIndex++) {if (in[rootIndex] == post[postEnd]) // 在中序遍历中找到根节点位置break;}int leftLength = rootIndex - inStart; // 左子树长度root->lchild = InPostCreateBiTree(in, post, inStart, rootIndex - 1, postStart, postStart + leftLength - 1); // 递归构造左子树root->rchild = InPostCreateBiTree(in, post, rootIndex + 1, inEnd, postStart + leftLength, postEnd - 1); // 递归构造右子树return root;
}int main() {ElemType in[] = {4, 7, 2, 1, 5, 3, 8, 6}; // 中序序列ElemType pre[] = {1, 2, 4, 7, 3, 5, 6, 8}; // 先序序列ElemType post[] = {7, 4, 2, 5, 8, 6, 3, 1}; // 后序序列ElemType level[] = {1, 2, 3, 4, 5, 6, 7, 8}; // 层序序列BiTree rootInPre = InPreCreateBiTree(in, pre, 0, 7, 0, 7);BiTree rootInPost = InPostCreateBiTree(in, post, 0, 7, 0, 7);// 中序加层序构造二叉树需要给定中序和层序序列，由于层序序列不是标准的输入序列，无法直接用现有函数构造，暂不实现printf("InPreOrder: ");PreOrder(rootInPre);printf("\n");printf("InOrder: ");InOrder(rootInPre);printf("\n");printf("InPostOrder: ");PostOrder(rootInPost);printf("\n");printf("LevelOrder: ");LevelOrder(rootInPre);printf("\n");return 0;
}