目录
- 向量链式法则
- 标量链式法则
- 拓展到向量
- 例题1
- 例题2
- 符号求导
- 数值求导
- 自动求导
- 计算图
- 自动求导的两种模式
- 链式法则
- 正向累积(从x出发)
- 反向累积(反向传递--先计算最终的函数即y)
- 反向累积总结
- 自动求导
- 计算y关于x的梯度,使用requires_grad(True)
- 计算y
- 通过调用反向传播函数来自动计算y关于x每个分量的梯度
- PyTorch会累积梯度,使用zero_()函数清除梯度
- 批量中每个样本单独计算的偏导数之和
- 将某些计算移动到记录的计算图之外
- 即使构建函数的计算图通过Python控制流仍可以计算变量的梯度
- 问题
- 多个loss(损失函数)分别反向的时候是不是需要累积梯度?
- 需要正向和反向都要算一遍吗?
- 为什么Pytorch会默认累积梯度?
- 为什么获取.grad前需要backward?
向量链式法则
标量链式法则
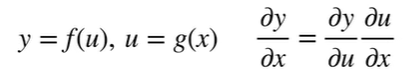
拓展到向量
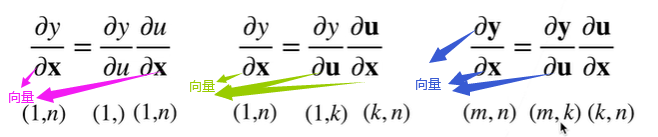
例题1
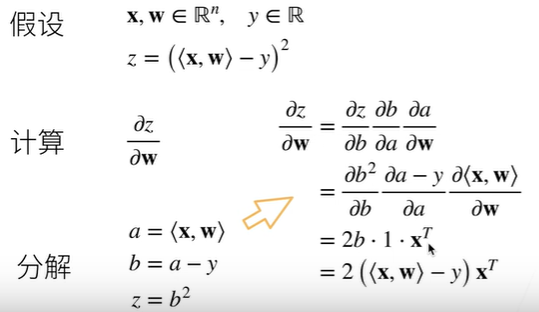
过程:
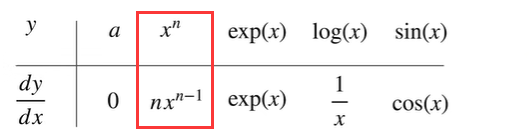
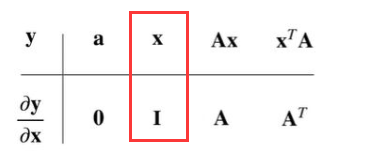
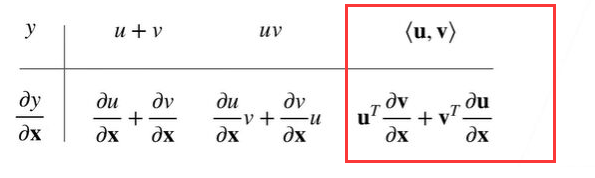
例题2
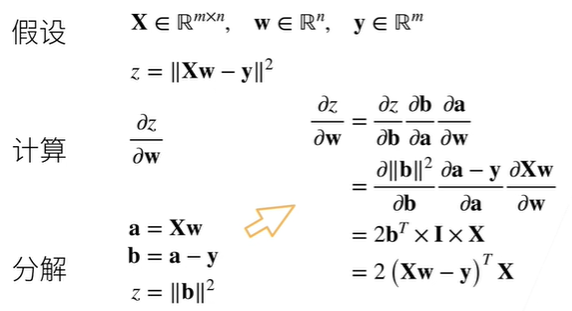
过程:
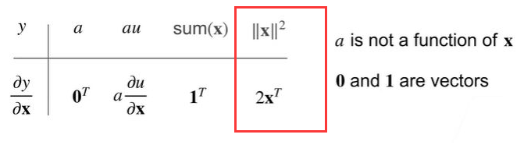
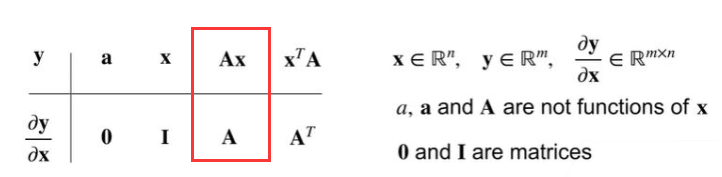
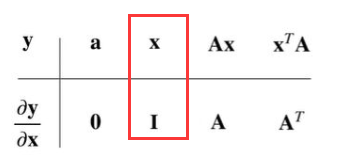
然后将分解的回代
符号求导
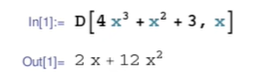
数值求导
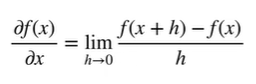
自动求导
自动求导计算一个函数在指定值上的导数
计算图
将代码分解为操作子
将计算表示成一个无环图
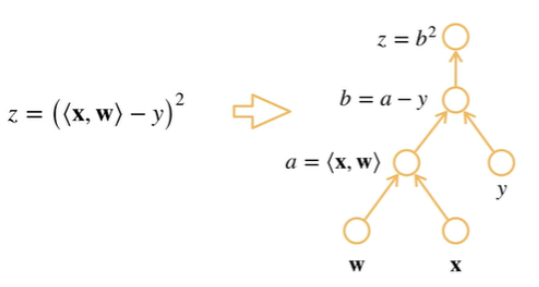
显示构造

隐式构造
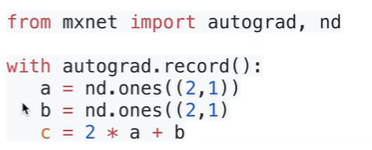
自动求导的两种模式
链式法则
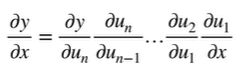
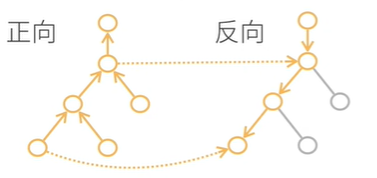
正向累积(从x出发)
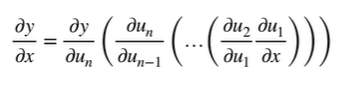
反向累积(反向传递–先计算最终的函数即y)
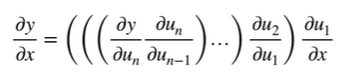
这里的反向先计算z的函数
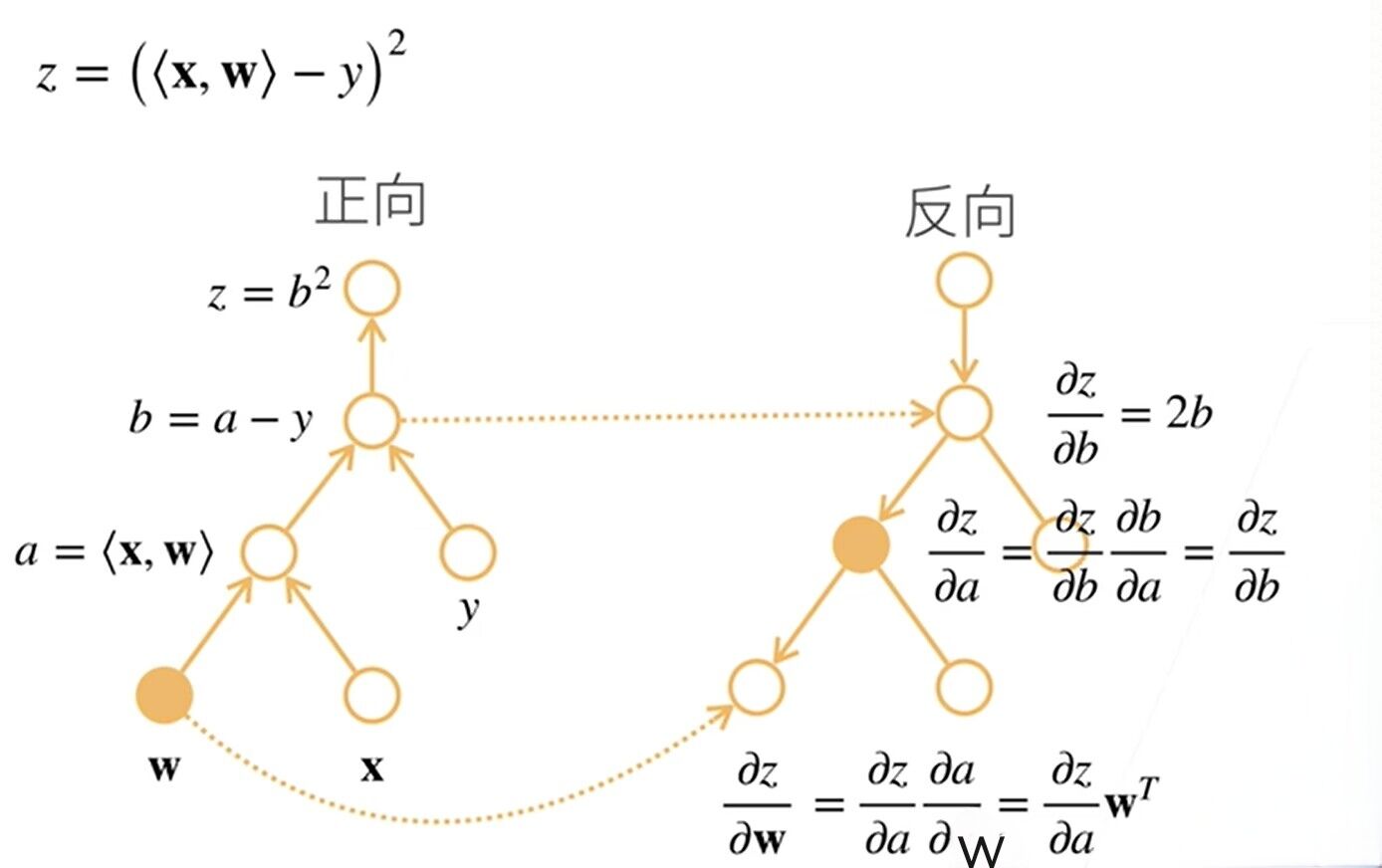
反向累积总结
构造计算图
前向:执行图,存储中间结果
反向:从相反方向执行图
去除不需要的枝
计算复杂度:O(n),n是操作子个数
通常正向和方向的代价类似
内存复杂度:O(n),因为需要存储正向的所有中间结果
正向累积:
它的内存复杂度是O(1),即不管多深我不需要存储它的结果,而反向累积则需要存储。
反向从根节点向下扫,可以保证每个节点只扫一次;
正向从叶节点向上扫,会导致上层节点可能需要被重复扫多次。
(正向中 子节点比父节点先计算,因此也无法像反向那样把本节点的计算结果传给每个子节点。)
自动求导
假设我们对函数 y=2 x T x^T xTx 求导
import torch
x = torch.arange(4.0)
print(x)
结果:
计算y关于x的梯度,使用requires_grad(True)
import torch
x = torch.arange(4.0, requires_grad=True)
print(x.grad)
结果: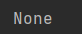
计算y
import torch
x = torch.arange(4.0, requires_grad=True)
y = 2 * torch.dot(x, x)
print(y)
结果:
通过调用反向传播函数来自动计算y关于x每个分量的梯度
import torch
x = torch.arange(4.0, requires_grad=True)
print(x)
y = 2 * torch.dot(x, x)
y.backward() #求导
print(x.grad) #x.grad访问导数
结果:
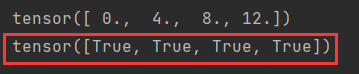
y=2 x 2 x^2 x2然后使用求导函数backward()实质是y导=4x(下面验证)。
import torch
x = torch.arange(4.0, requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward() #求导
print(x.grad == 4*x)
结果:
PyTorch会累积梯度,使用zero_()函数清除梯度
import torch
x = torch.arange(4.0, dtype=torch.float32, requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward()
print(x.grad)x.grad.zero_() #梯度清零
y = x.sum()
y.backward() #求导
print(x.grad)
因为求向量的sum()所以梯度是全1
y是标量
y是对x的的求和:y= x 1 x_1 x1+ x 2 x_2 x2+ x 3 x_3 x3+ x 4 x_4 x4。
对y进行x的偏导:dy/ d x 1 dx_1 dx1,dy/ d x 2 dx_2 dx2,dy/ d x 3 dx_3 dx3,dy/ d x 4 dx_4 dx4
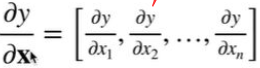
批量中每个样本单独计算的偏导数之和
import torch
x = torch.arange(4.0, dtype=torch.float32, requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward()
print(x.grad)x.grad.zero_() #梯度清零,如果不清零执行y=x*x然后对y求和再求导可以通过x.grad查看得[0.,1.,4.,*.]
y = x*x #x是向量,y即向量
print(y) #输出查看
y.sum().backward() #求导
print(x.grad)
梯度(求导)清零:必须先存在梯度,如果没有y.backward()则x.grad.zero_()会报错。
结果:
将某些计算移动到记录的计算图之外
import torch
x = torch.arange(4.0, dtype=torch.float32, requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward()
print(x.grad)x.grad.zero_() #梯度清零,如果不清零执行y=x*x然后对y求和再求导可以通过x.grad查看得[0.,1.,4.,*.]
y = x * x #x是向量,y即向量
print(y) #输出查看
u = y.detach()#把y当作一个常数,而不是关于x的函数,把它做成u
z = u * x #相当于z=常数*x
z.sum().backward()
print(x.grad == u)
结果:这里的z就是为了后续求导检查是否与detach()后一致。

import torch
x = torch.arange(4.0, dtype=torch.float32, requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward()
print(x.grad)x.grad.zero_() #梯度清零,如果不清零执行y=x*x然后对y求和再求导可以通过x.grad查看得[0.,1.,4.,*.]
y = x * x #x是向量,y即向量
y.sum().backward()
print(x.grad == 2 * x)
结果:
即使构建函数的计算图通过Python控制流仍可以计算变量的梯度
import torchdef f(a):b = a * 2while b.norm() < 1000:#norm()计算张量的范数, 计算了张量 b 的L2范数b = b * 2if b.sum(): #检查 b 所有元素的总和是否非零c = b #非0的时候的操作else:c = 100 * breturn ca = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
print(a.grad == d / a) #梯度验证
结果: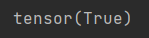
问题
多个loss(损失函数)分别反向的时候是不是需要累积梯度?
是的
需要正向和反向都要算一遍吗?
是的
为什么Pytorch会默认累积梯度?
设计上的理念,通常一个大的批量无法一次计算出,所以分为多次,然后累加起来。
为什么获取.grad前需要backward?
不进行backward时不会计算梯度,因为计算梯度是一个很“贵”的事情