容斥原理
背景:两个集合相交
高中的韦恩图,我们知道两个集合相交时我们可以通过简单的计算来认识相关的性质
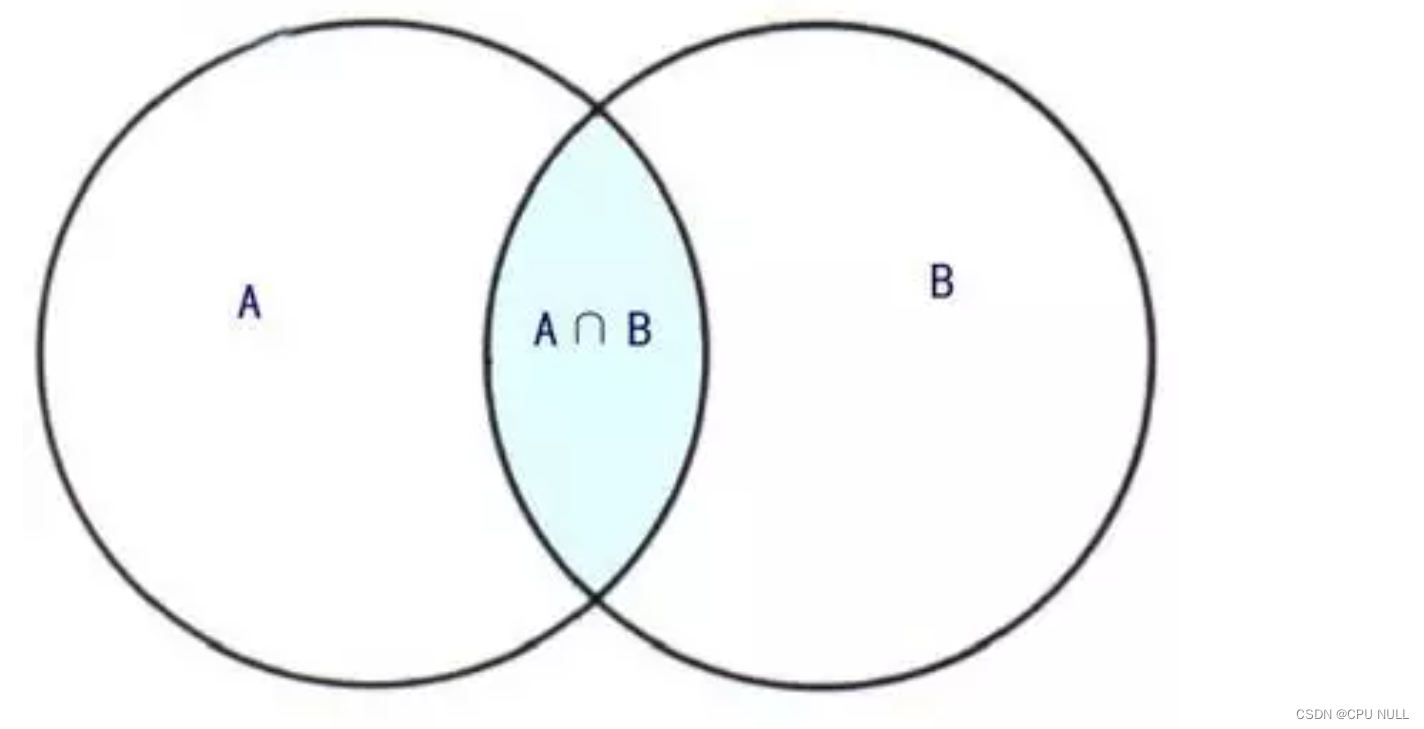
集合相交的区域是 A ∩ B A\cap B A∩B ,集合的并集是 A ∪ B A\cup B A∪B ,那怎么用集合表示 A ∪ B A\cup B A∪B
我们可以看作是A集合和B集合相加,但明显中间的 A ∩ B A\cap B A∩B 加了两次,因此要减去
所以 A ∪ B A\cup B A∪B= A + B − A ∩ B A+B-A\cap B A+B−A∩B
容斥原理:如果是三个或多个集合相交我们该怎么做
这时候就要用到容斥原理这个知识了
三个集合相交:

多个集合相交:
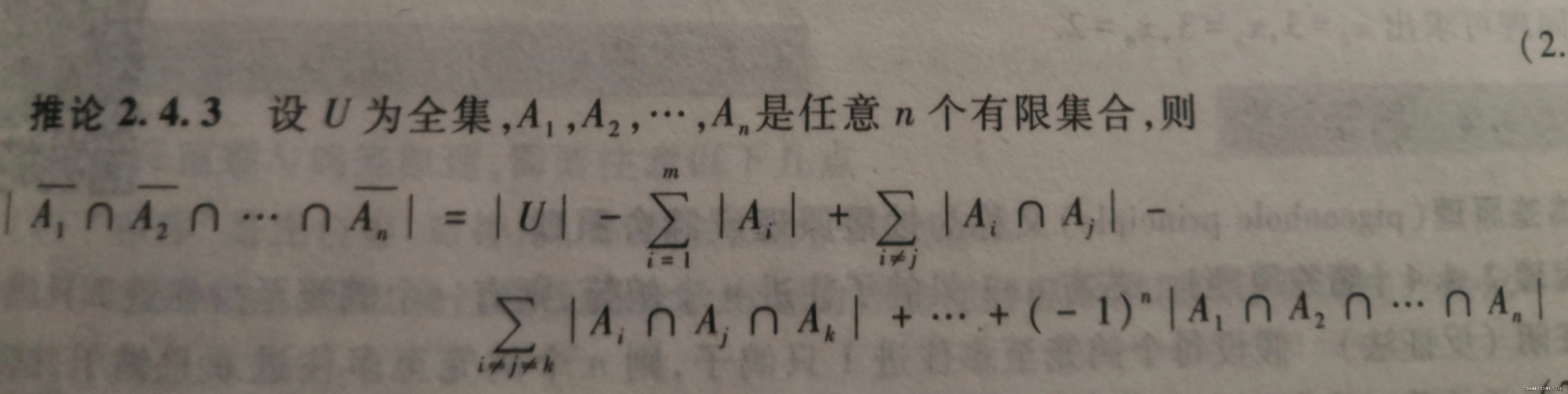
我们接下来重点探讨三个集合相交的情况

先让 S 1 , S 2 , S 3 S_1,S_2,S_3 S1,S2,S3相加,但是红绿区域多加了一次,红紫区域和绿紫区域都是多加了一次,所以我们就要减去
S 1 ∩ S 2 , S 2 ∩ S 3 , S 1 ∩ S 3 S_1\cap S_2,S_2\cap S_3,S_1\cap S_3 S1∩S2,S2∩S3,S1∩S3 ,原先最中间的红绿紫区域多加了两次,但减去时减了三次,相当于最中间区域多减了一次,那么我们要加回来,即加上 S 1 ∩ S 2 ∩ S 3 S_1\cap S_2 \cap S_3 S1∩S2∩S3,最终结果如上图所示。
相关题目
幸运数
如果一个整数能够被 6 或 8整除,就称该整数为一个幸运数。
给定整数 n,请你计算 1到n范围内的幸运数的数量。
输入格式
一个整数 n。
输出格式
一个整数,表示 1到n范围内的幸运数的数量。
数据范围
前 3 个测试点满足 1≤n≤10。
所有测试点满足 1≤n≤100。
输入样例:
10
输出样例:
2
题解:
这道题看数据量很小,思路简单,直接遍历方便且怎么写都不会超时
于是暴力代码:
#include<bits/stdc++.h>
using namespace std;
int ans;
int main()
{ int n;cin>>n;for(int i=1;i<=n;i++){if(i%6==0||i%8==0)ans++;}cout<<ans;return 0;
}
容斥原理法
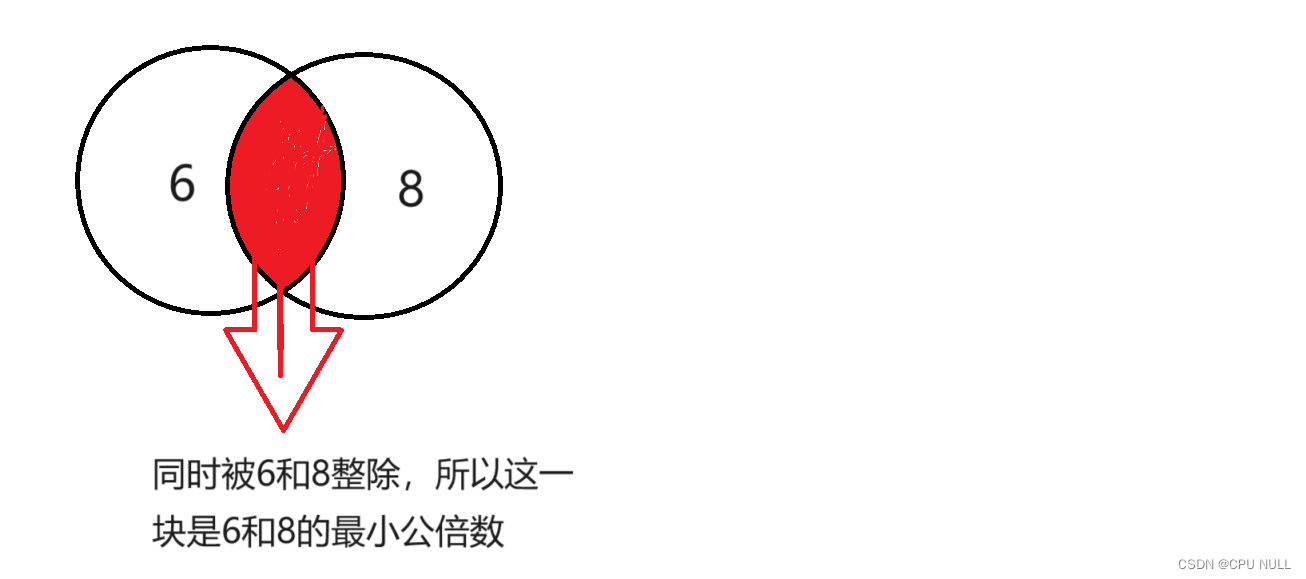
n个数里面有多少个被8整除:n/8个(计算机int 向下取整,n/8所得结果就是答案)
为什么这样算:从1到n,每8个数为一循环是8的倍数,8,16,24, 。。。等,不足8的不能计入
所以可以用==总的个数 − - − n / 8 n/8 n/8- n / 6 − n / 24 ( 24 为 6 和 8 的最小公倍数 ) n/6-n/24(24为6和8的最小公倍数) n/6−n/24(24为6和8的最小公倍数)
#include<bits/stdc++.h>
using namespace std;
int ans;
int main()
{ //容斥原理:int n;cin>>n;cout<<n/6+n/8-n/24<<endl;return 0;
}
三个集合下容斥原理的应用
那如果是三个集合呢,下一题是三个集合时对于我们的容斥原理的应用
不想被排除
题目描述
给出一个数 n 以及 x , y , z ,求 1 到 n 中,有多少个数不是 x, y, z 中任意一个数的倍数。
输入格式
第一行输入一个整数 T,表示测试组数( 1 ≤ T ≤ 1 0 5 1≤T≤10^5 1≤T≤105 ).
接下来会有 T 行输入,每行 4 个整数 n, x*, y*, z*( 1 ≤ n ≤ 1 0 18 , 1 ≤ x , y , z ≤ 1 0 6 1≤n≤10^{18}, 1≤x,y,z≤10^{6 } 1≤n≤1018,1≤x,y,z≤106).
输出格式
共 𝑇T 行,每行输出一个整数,表示 1 到 n 中,不是 x, y*, z* 中任意一个数倍数的整数个数。
测试样例
输入数据 1
2
10 3 4 5
100 2 4 6
输出数据 1
3
50

题目分析:
S 1 看作被 x 整除, S 2 看作被 y 整除 , S 3 看作被 z 整除,那么 S 1 ∩ S 2 则看作被 x 和 y 整除 S_1看作被x整除,S_2看作被y整除,S_3看作被z整除,那么S_1\cap S_2则看作被x和y整除 S1看作被x整除,S2看作被y整除,S3看作被z整除,那么S1∩S2则看作被x和y整除
S 1 ∩ S 3 看作被 x 和 z 整除, S 2 ∩ S 3 看作被 y 和 z 整除, S 1 ∩ S 2 ∩ S 3 看作同时被 x , y , z 整除 S_1\cap S_3看作被x和z整除,S_2\cap S_3看作被y和z整除,S_1\cap S_2\cap S_3看作同时被x,y,z整除 S1∩S3看作被x和z整除,S2∩S3看作被y和z整除,S1∩S2∩S3看作同时被x,y,z整除
所以问题就简化为用总个数减去 ①被x和y整除,②被x和z整除,③被y和z整除,④同时被x,y,z整除的数的个数
这里的点是如何求 S 1 ∩ S 2 ∩ S 3 S_1\cap S_2\cap S_3 S1∩S2∩S3 ,即x,y,z三个数的最小公倍数
这里直接借用CSDN大佬的解决办法:即先求x,y的最小公倍数 L C M ( x , y ) ,再求 z 和 L C M ( x , y ) 的最小公倍数 L C M ( L C M ( x , y ) , z ) LCM(x,y),再求z和LCM(x,y)的最小公倍数LCM(LCM(x,y),z) LCM(x,y),再求z和LCM(x,y)的最小公倍数LCM(LCM(x,y),z)

#include<bits/stdc++.h>
using namespace std;
#define int long longint gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);
}
signed main()
{ int t,n,x,y,z;cin>>t;while(t--){scanf("%lld%lld%lld%lld",&n,&x,&y,&z);int a1=(x*z)/gcd(x,z);//x和z的最小公倍数int a2=(y*z)/gcd(y,z);//y和z的最小公倍数int a3=(x*y)/gcd(x,y);//x和y的最小公倍数a3int a4=(a3*z)/gcd(a3,z);//a3和z的最小公倍数printf("%lld\n",n-(n/x+n/y+n/z+n/a4-n/a1-n/a2-n/a3));//总个数减去 ①被x和y整除,②被x和z整除,③被y和z整除,④同时被x,y,z整除的数的个数}return 0;
}