Leetcode算法训练日记 | day37-编程知识

专题九贪心算法

一、单调递增的数字

1.题目

Leetcode：第 738 题

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回小于或等于 n 的最大数字，且数字呈 单调递增 。

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

2.解题思路

使用贪心算法解决单调递增的数字问题。

在 monotoneIncreasingDigits 函数中，首先将整数 N 转换为字符串 strNum。然后，我们使用两个 for 循环来找到并修改数字。第一个 for 循环从字符串的末尾开始向前遍历，寻找第一个不满足单调递增条件的位置。一旦找到这样的位置，我们记录下这个位置，并将其前一个位置的数字减 1，因为我们知道这个数字太大，导致无法通过简单地将后面的数字置为 9 来得到下一个更大的单调递增数字。第二个 for 循环从记录的位置开始，将后面的所有数字置为 9。这是因为在第一个 for 循环中，我们已经确保了前面的数字是单调递增的，所以我们只需要简单地增加后面的数字。最后，我们使用 stoi 函数将修改后的字符串 strNum 转换回整数，并返回这个新的整数。这个新的整数就是满足条件的下一个更大的单调递增数字。

3.实现代码

#include <iostream>
#include <vector>
#include <string>
using namespace std;class Solution {
public:// monotoneIncreasingDigits 函数用于找到一个数字 N 的下一个更大的单调递增数字int monotoneIncreasingDigits(int N) {// 将整数 N 转换为字符串，以便逐位操作string strNum = to_string(N);// 初始化 flag 变量，用于标记从哪个位置开始可以将数字置为 9// 默认设置为字符串的长度，即最开始不需要置任何数字为 9int flag = strNum.size();// 从字符串的末尾开始向前遍历，找到第一个不是严格递增的位置for (int i = strNum.size() - 1; i > 0; i--) {// 如果当前位的数字大于下一位，说明找到了一个递减的位置if (strNum[i - 1] > strNum[i]) {// 记录这个位置，从这个位置开始，可以置后面的所有数字为 9flag = i;// 将当前位置的数字减 1，因为当前位置的数字太大，导致后面的数字无法通过置为 9 来增加strNum[i - 1]--;}}// 从记录的位置开始，将后面的所有数字置为 9for (int i = flag; i < strNum.size(); i++) {strNum[i] = '9';}// 将修改后的字符串转换回整数，并返回return stoi(strNum);}
};//测试
int main()
{Solution p;int n = 1234;cout <<"n = " <<n<< endl;int result = p.monotoneIncreasingDigits(n);cout << "小于或等于 n 的最大数字:" << result << endl;cout << endl;return 0;
}

二、监控二叉树

1.题目

Leetcode：第 738 题

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

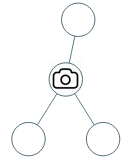
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

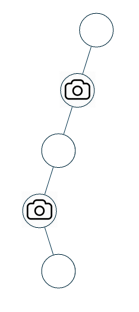
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

2.解题思路

使用贪心算法解决监控二叉树问题。

在 minCameraCover 函数中，我们首先初始化 result 为 0，表示还没有放置任何摄像头。然后，我们调用 traversal 函数从根节点开始递归遍历二叉树。traversal 函数的返回值决定了当前节点及其子节点的覆盖状态。traversal 函数中，我们首先检查当前节点是否为空，如果为空，返回 2。然后，我们递归地遍历左子树和右子树，并获取它们的返回值。根据这些返回值，我们可以确定当前节点是否需要一个摄像头，以及如何继续递归地遍历子树。如果 traversal 函数返回 0，表示根节点及其子节点都被摄像头覆盖了，我们不需要在根节点放置摄像头。否则，我们需要在根节点放置一个摄像头，并增加 result 的值。最终，minCameraCover 函数返回 result，即覆盖整个二叉树所需的最小摄像头数量。

3.实现代码

#include <iostream>
#include <vector>
#include <string>
using namespace std;// 定义一个结构体TreeNode，用于表示二叉树的节点。
struct TreeNode {int val; // 存储节点的值。TreeNode* left; // 指向该节点左子树的指针。TreeNode* right; // 指向该节点右子树的指针。// TreeNode的构造函数，用于创建一个TreeNode实例。// 参数x是节点的值，left和right默认为NULL，表示没有左右子节点。TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class Solution {
private:int result; // 用于存储最终的摄像头数量// traversal 函数用于递归遍历二叉树，返回值有特定的含义：// 返回 0 表示该节点及其子节点都不需要摄像头（叶子节点或其子节点都被摄像头覆盖）// 返回 1 表示该节点需要一个摄像头（其子节点都被摄像头覆盖）// 返回 2 表示该节点不需要摄像头，但其子节点需要摄像头int traversal(TreeNode* cur) {if (cur == NULL) return 2; // 如果当前节点为空，返回 2int left = traversal(cur->left);    // 递归遍历左子树，并获取返回值int right = traversal(cur->right);  // 递归遍历右子树，并获取返回值// 如果左右子树返回的值都是 2，说明当前节点不需要摄像头，其子节点也不需要if (left == 2 && right == 2) return 0;// 如果左子树或右子树返回的值是 0，说明该子树被摄像头覆盖，当前节点需要一个摄像头else if (left == 0 || right == 0) {result++; // 增加摄像头数量return 1; // 返回 1 表示当前节点需要一个摄像头}else return 2; // 如果到这里，说明当前节点的子节点都需要摄像头，当前节点也不需要}public:// minCameraCover 函数用于计算在二叉树上最小数量的摄像头以覆盖所有节点int minCameraCover(TreeNode* root) {result = 0; // 初始化摄像头数量为 0// 从根节点开始遍历二叉树if (traversal(root) == 0) { // 如果根节点返回 0，说明根节点无覆盖result++; // 根节点需要一个摄像头}return result; // 返回最终的摄像头数量}
};

ps：以上皆是本人在探索算法旅途中的浅薄见解，诚挚地希望得到各位的宝贵意见与悉心指导，若有不足或谬误之处，还请多多指教。