有些事情本来很遥远,你争取,它就会离你越来越近
- 概念 + 名词解释
- 如何理解递归
- dfs 回溯类问题
- 蓝桥杯——飞机降落
- dfs 迷宫搜索类问题
- 蓝桥杯——岛屿个数
概念 + 名词解释
递归是指在一个函数的定义中调用自身的过程,有些复杂问题可以划分为多个相同子问题的话,就可以大概率可以使用递归来解决。经典算法如暴搜、回溯、深度优先遍历(dfs)、FloodFile算法、记忆化搜索等本质上都是使用递归来解决,换句话来说,这些本质上来说都是一种问题。
如何理解递归
初学者可以在做递归简单问题的时候,画递归展开图来帮助理解递归,如斐波那契数列问题 f(n) = f(n - 1) + f(n - 2),要求出f(4),就得先递归去求解 f(3)和 f(2);
当学习了数据结构之后呢,可以做一些二叉树相关的 OJ 题目去理解递归,但二叉树刚开始做其实都是非常迷的,但慢慢理解后,好像确实就只是这么个事哈哈。
当做了一些简单递归题目和二叉树后,就可以尝试从宏观上理解递归了,可以将递归问题分为三步:
- 不细想递归展开图,越复杂的问题越不能画递归展开图,递归展开图只适用于在简单题中理解递归
- 把递归的函数想象成一个
黑盒,你让这个黑盒去完成一个任务,并信任这个黑盒一定能完成。只需要设计好这个黑盒即可! - 将复杂问题的主逻辑写出来,只在乎递归的结果,并将这个问题解决
那么问题就变为了,如何设计递归函数,也就是如何设计一个这样的黑盒?
首先,找到题目中的多个相同子问题——递归函数头的设计
只关心其中一个子问题是如何解决的——递归函数体的设计
根据经验或题目要求再确定一下递归的出口即可
单看比较抽象,使用一个例子来解释一下上面的步骤:
面试题——汉诺塔
汉诺塔问题,大家都听过吧,将多个圆盘从一个柱A 借助 柱B 移动到 柱C,前提是不小的盘子必须放在大的盘子的上面,问一共有多少种解法?
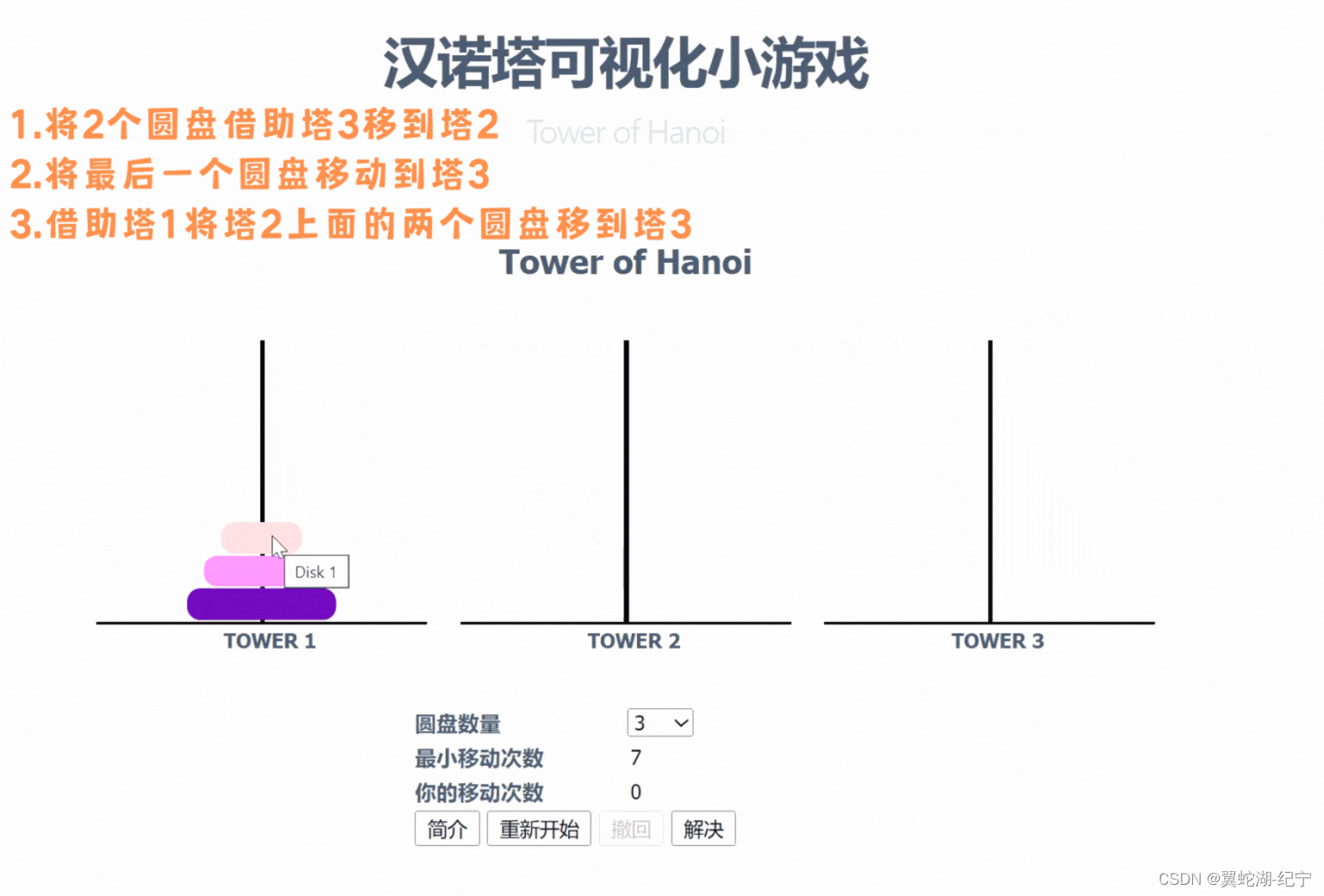
当然汉诺塔问题是有公式解决的的,但这没有任何意义,我们的目的是从宏观上理解递归。
当有n个圆盘的时候,我们可以先将(n-1)个圆盘移动到 塔2 上面,然后再将塔1的最后一个大圆盘移至 塔3,再用同样的方法将塔2上的(n-1)个元素借助塔1移至塔3,要将这 n - 1 个移动,就要先移动 n - 2,如此往复…
找到了重复子问题:要移动 n 个,就要先解决 n - 1 个怎么搞,要解决 n - 1 个,就要先解决 n - 2 个怎么搞…,并且函数头需要将这几个柱子全部传过去

那么其中一个子问题需要怎么解决呢?
假设有 3个柱子ABC吗,n 个盘子,那么需要先将 n - 1 个盘子借助 C 先移动到 B,再将地下那个最大的移动到 C ,然后A 空了,再借助 A 将 B 上的 n - 1 个盘子移动到 C上,就完成了任务。说明在 n 减到 1 之前,都需要重复上面的步骤,先将 n -1 个盘子借助一个柱子移动到另一个上,然后将第 n 个移动。那么函数体的设计:


那么,在 n > 1 的时候就要一直递归,直到 n = 1 时才进行第一次返回,所以递归出口就是 n == 1,递归返回前,需要将盘子从 A 移动到 C,然后返回。

汉诺塔力扣代码:
class Solution {
public:void _haota(vector<int>& A, vector<int>& B, vector<int>& C, int n){if(n == 1){C.push_back(A.back());A.pop_back();return;}_haota(A, C, B, n - 1);C.push_back(A.back());A.pop_back(); _haota(B, A, C, n - 1);}void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {int n = A.size(); // 需要移动的盘子数量_haota(A, B, C, n);}
};
其实我也不知道自己到底说没说明白…
dfs 回溯类问题
步骤:
先使用决策树画出所有情况,如对 [1, 2, 3] 进行全排列
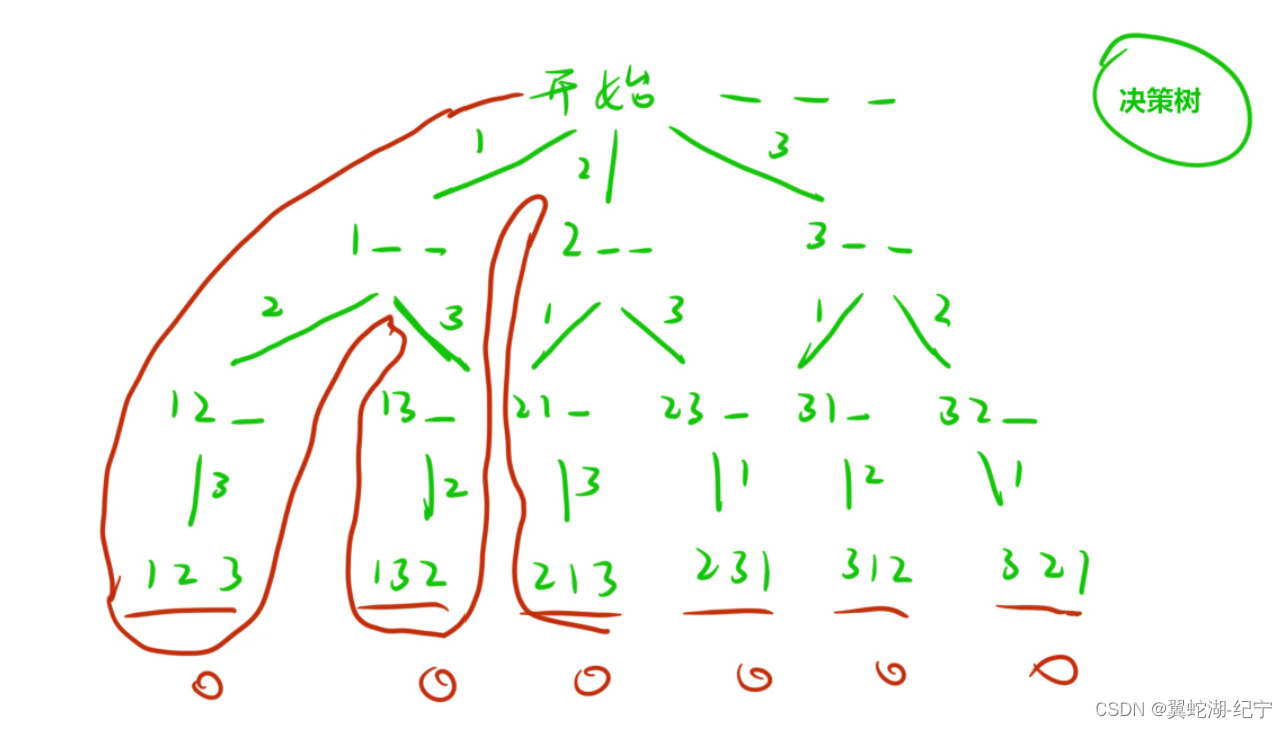
使用 全局变量path 来记录某条路径上的结果,在决策树画到底部的时候,判断 path 中的结果是否符合结果,然后需要“向上返回”,并且顺便“恢复现场”,如上图中,path 中在底部变成了 123,恢复现场后就成了 12;如果没有可以继续走的路,就继续“向上返回”,再恢复现场,然后判断是否有其他路径可以走,遍历完决策树中所有情况后,就暴搜出了所有情况。
剪枝
即剪去不合理的分支,当全排列的时候,某个数字被列举了之后,就不能再使用了,因此要剪去这个分支!一般我们可以使用 bool 类型的check[] 数组来实现剪枝。
全排列力扣代码
class Solution {
public:vector<vector<int>> ret;vector<int> path;bool check[7] = { false };vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size() == nums.size()){ret.push_back(path); // 将合理路径放入最终结果return;}for(int i = 0; i < nums.size(); i++){if(!check[i]){check[i] = true;path.push_back(nums[i]);dfs(nums);check[i] = false; // 恢复现场path.pop_back(); // 恢复现场}}}
};
蓝桥杯——飞机降落



这道题的数据要求不算高,我们就可以考虑将所有情况都枚举一遍,也就是暴搜!
#include<bits/stdc++.h>
using namespace std;
// 飞机降落
struct plane
{int a; // 到达时间 int b; // 可以盘旋的时间 int c; // 降落所需的时间
};int T; // 组数
int N; // 每组的飞机数
plane vp[12];
bool check[12];
bool dfs(int num, int last)//num 为第几个, last 为上一架的降落时间
{if(num == N){return true;// 能走到这一步,说明符合题意且结束了 }for(int i = 0; i < N; i++){if(!check[i] && vp[i].a + vp[i].b >= last)// 说明可以降落 {check[i] = true;if(dfs(num + 1, max(last, vp[i].a) + vp[i].c)) return true;check[i] = false;}}return false;// 全部都遍历, 如果没有满足情况的话, 说明不行, 就返回
}
int main()
{cin >> T; // 组数for(int i = 0; i < T; i++){cin >> N;for(int i = 0; i < N; i++){cin >> vp[i].a >> vp[i].b >> vp[i].c;}if(dfs(0, 0)) cout << "YES" << endl;else cout << "NO" << endl;}return 0;
}
dfs 迷宫搜索类问题
搜索类问题一般都是在二维矩阵中进行,以某个坐标为起点进行一次/多次深度优先遍历,直到遇到某个位置停止。
在二维矩阵中搜索,一般可以定义两个向量数组
// 当题目要求只能上下左右四个方向走时int dx[4] = { 0, 0, 1, -1 };int dy[4] = { 1, -1, 0, 0 };// 如当前的位置坐标为 (i, j), 那么可以走的位置有:(矩阵 m 行 n 列)for(int k = 0; k < 4; k++){int x = dx[k] + i, int y = dy[k] + j;if(x >= 0 && x < m && y >= 0 && y < n && !visit[x][y] && /* 题目要求条件*/){visit[x][y] = true;dfs(x, y, /**/);}}
// 当题目要求可以上下左右、斜左上、斜右上、斜左下、斜右下这8个方向走时int dx[4] = { 0, 0, 1, -1 , 1, 1, -1, -1};int dy[4] = { 1, -1, 0, 0 , -1, 1, -1, 1};for(int k = 0; k < 8; k++){int x = dx[k] + i, int y = dy[k] + j;if(x >= 0 && x < m && y >= 0 && y < n && !visit[x][y] && /* 题目要求条件*/){visit[x][y] = true;dfs(x, y, /**/);}}
还会定义一个 visit[][] 数组,用来记录某个位置是否被遍历过了
力扣练习题——黄金矿工
参考代码:
class Solution {
public:// 当题目要求只能上下左右四个方向走时int dx[4] = { 0, 0, 1, -1 };int dy[4] = { 1, -1, 0, 0 };// 当题目要求可以上下左右、斜左上、斜右上、斜左下、斜右下这8个方向走时int dx[4] = { 0, 0, 1, -1 , 1, 1, -1, -1};int dy[4] = { 1, -1, 0, 0 , -1, 1, -1, 1};bool visit[16][16] = { false };int ret = 0;int getMaximumGold(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();int gold = 0;for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (grid[i][j] != 0){visit[i][j] = true;gold += grid[i][j];dfs(grid, i, j, gold);gold -= grid[i][j];visit[i][j] = false;}}}return ret;}void dfs(vector<vector<int>>& grid, int i, int j, int gold){for (int k = 0; k < 4; k++){int x = i + dy[k], y = j + dx[k];if (x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() &&grid[x][y] != 0 && !visit[x][y]) {gold += grid[x][y];visit[x][y] = true;dfs(grid, x, y, gold);gold -= grid[x][y];visit[x][y] = false;}}ret = max(ret, gold);return;}
};
蓝桥杯——岛屿个数




int T;
int M, N;
int nums[12][12];
bool visit[12][12];
int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};
int dxx[8] = {0, 0, 1, -1, 1, 1, -1, -1};
int dyy[8] = {1, -1, 0, 0, -1, 1, 1, -1};
int ret = 0;
void dfs_board(int i, int j)
{for(int k = 0; k < 4; k++){int x = i + dx[k];int y = j + dy[k];if(x >= 1 && x <= M && y >= 1 && y <= N && !visit[x][y] && nums[x][y] == 1){visit[x][y] = true; // 遍历陆地 dfs_board(x, y);}}
}
void dfs_sea(int i, int j)
{for(int k = 0; k < 8; k++){int x = i + dxx[k];int y = j + dyy[k];if(x >= 1 && x <= M && y >= 1 && y <= N && !visit[x][y] && nums[x][y] == 0){visit[x][y] = true; // 将外海全部标出来 dfs_sea(x, y);}if(x >= 1 && x <= M && y >= 1 && y <= N && !visit[x][y] && nums[x][y] == 1) {visit[x][y] = true;ret ++; // 陆地数量 + 1 dfs_board(x, y); // 当遇到陆地的时候,就去搜索这个陆地的连通块 }}
}
int main()
{cin >> T;while(T--){ret = 0;memset(nums, 0, sizeof(nums));memset(visit, 0, sizeof(visit));cin >> M >> N;for(int i = 1; i <= M; i++) // 将数据存入 nums 二维数组 {string str;cin >> str;for(int j = 1; j <= N; j++){nums[i][j] = str[j - 1] - '0'; // 将数据输入,只有 0 和 1 }}int flag = 0;for(int i = 1; i <= M; i++){for(int j = 1; j <= N; j++){if((i == 1 || i == M || j == 1 || j == N) && nums[i][j] == 0 && !visit[i][j]) // 在边缘位置找外海 {flag = 1;visit[i][j] = true;dfs_sea(i, j); // 从外海往进渗透,有8个方向 } }}if(flag == 0) ret = 1;cout << ret << endl;}return 0;
}