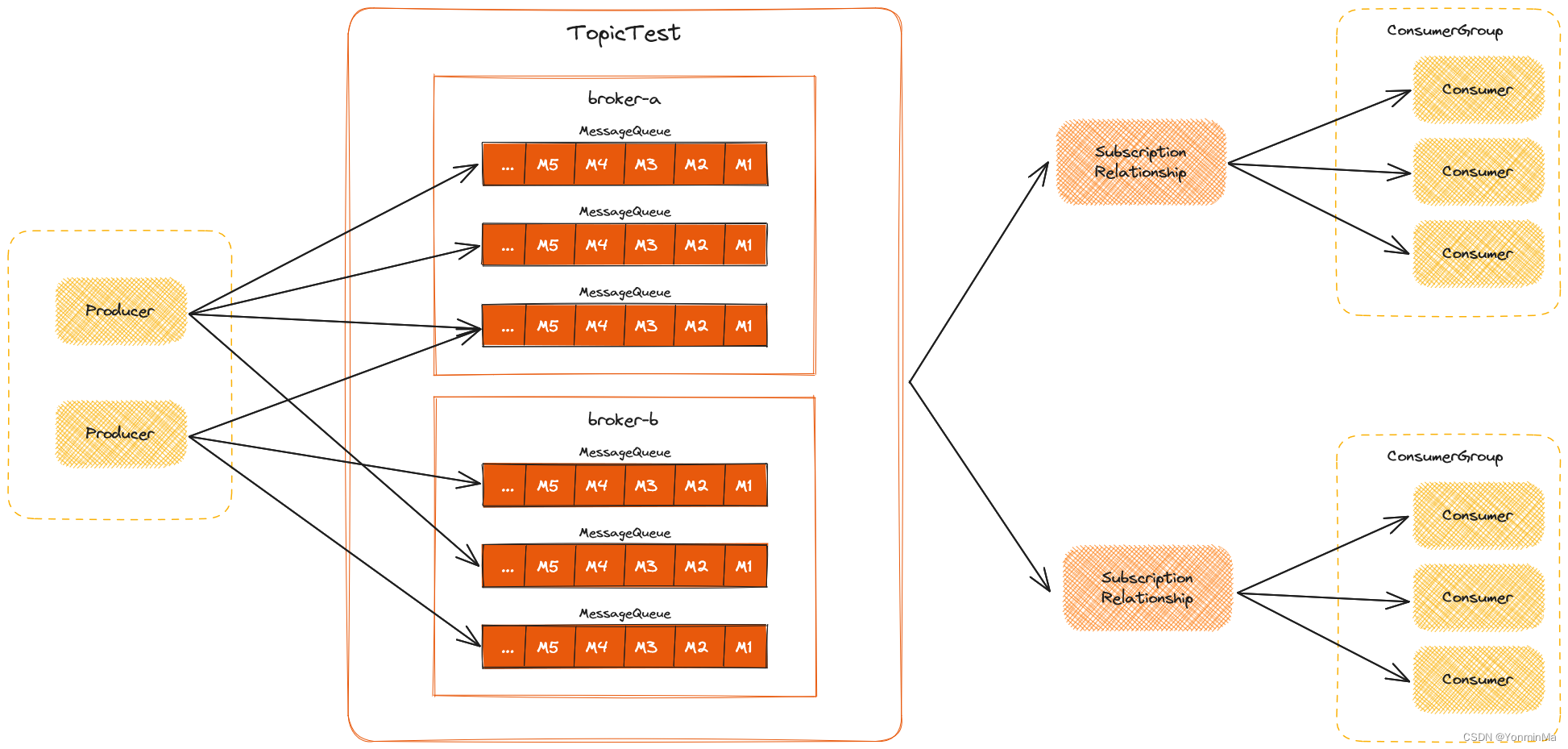
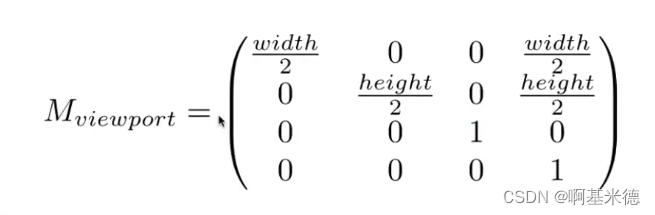MV矩阵(模型视图变换)
目的,把摄像机通过变换移动的世界坐标远点,并且朝向与Z轴的负方向相同。这个变换就是模型试图变换。
因为移动了相机,如果想保持正确的渲染的话,那么对应的物体需要要和相机保持相对运动,即模型也要经过
模型试图变换。

我们把上面的那个egt的交点,当作相机位置,T为相机的上方向,g为相机正方向的。
我们首先需要做的就是经过一系列变换,让它G与下面坐标系中-Z重叠,t与坐标系Y重叠,
相机点e与坐标原点重叠。
假设e的坐标为(Xe,Ye,Ze)。
首先我们需要移动相机位置到原点,使用一个平移矩阵
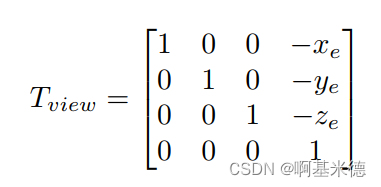
然后需要分别t旋转到Y, g旋转到-Z。但是我们直接旋转很困难。又因为
1.正向旋转一个角度的矩阵等于,负向旋转一个角度的矩阵的逆矩阵
2.旋转矩阵是正交矩阵
3.正交矩阵的逆矩阵是矩阵的转置
所以我们可以计算出-Z到g的旋转矩阵,以及Y到t的旋转矩阵.
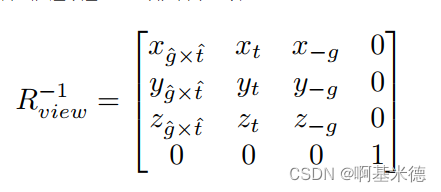
然后分别求出他们的转置,就是我们需要的旋转矩阵。
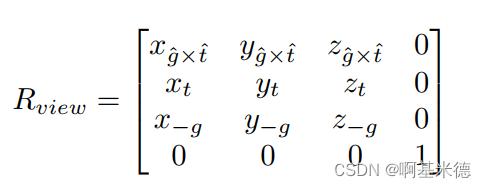
然后我们结合两个矩阵之后就可以得出我们需要的模型视图变换矩阵
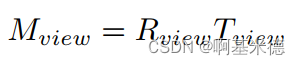
P矩阵(投影变换矩阵)
投影分为正交投影和透视投影,这两个是区别是是否有近大远小的效果。
正交投影投影变换:
首先把物体平移到远点,然后把缩放调整到-1,1,映射矩阵如下
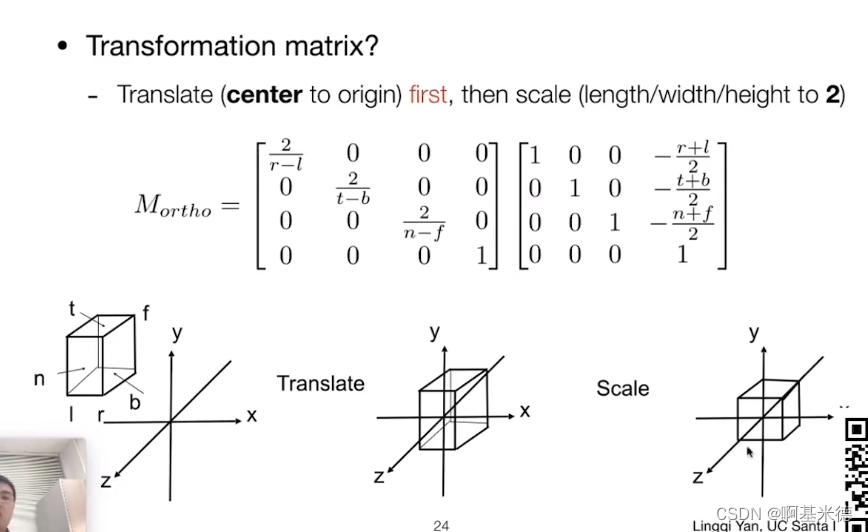
1.其中经过的是一个平移矩阵,把物体的坐标移动到原点。
2.然后经过一个缩放矩阵,把物体的大小缩放在-1到1的立方体空间内。
透视投影变换:
可以看作是原平面通过挤压变换成近平面,挤压前两个平面中的所有点会有一个映射关系,
我们需要计算出来这个映射关系并用矩阵形式表示出来,然后在经过一次正交投影的矩阵变化
就可以把四锥体远近平面内的物体映射到进平面中,这就是透视投影变换。
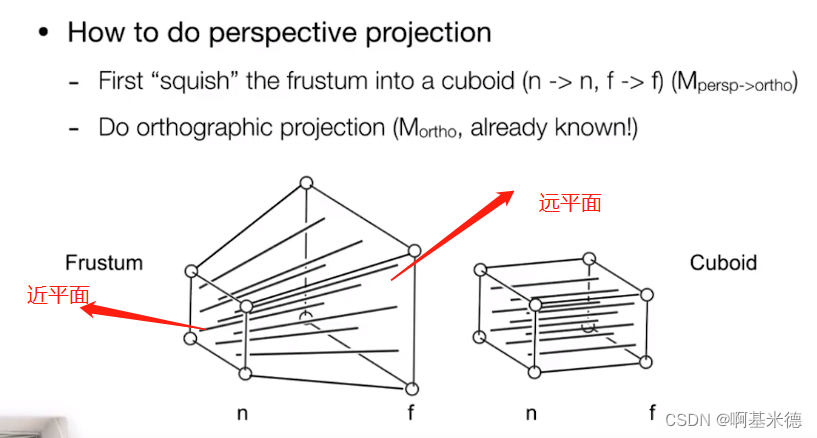
前提:
我们观察到压缩后远平面到近平面中间的距离不变,远平面中心点压缩后也不变化。
计算方式:
1.首先从侧试图看视锥体,我们可以得到视锥体中的点在经过压缩后 y 前后的关系如下

2.x坐标的变化和y雷同

注意:我们这儿的侧视图里面的点并不是都在z轴上(x 坐标等于0),所以z的坐标在上述中并不是不变的.
3.根据上面的对应关系,我们得出矩阵如下

4.根据远平面和近平面中Z的值不遍

推导除矩阵的第三行,如下:
<1>.近平面上的点Z不表带入我们上述的矩阵公式,可以得到第三行矩阵是(0 0 A B)

<2>.远平面中心点,压缩后不变,同样带入矩阵变换方程,至此我们就可以得到一个二元一次方程组:

可以得到
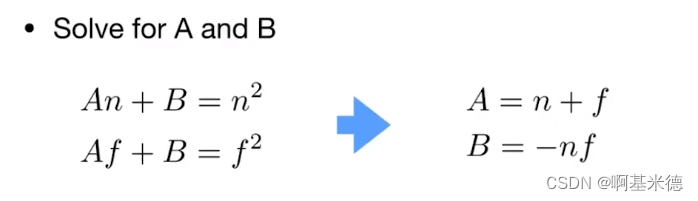
由于n,f是我们自己定义的相机的远近裁剪面,是已知的,所以我们可以得到该压缩的完整变换矩阵。
5.得到压缩矩阵之后再经过正交矩阵的就可以得到透视矩阵的矩阵变换了

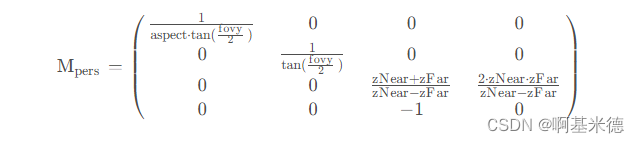
视口变换
以上的话MVP矩阵就算完成了。经过MVP矩阵的后的物体会放置在一个-1到1的视口中,但是我们最终目的是显示到屏幕上,那么我们就需要根据屏幕大小,把我们的视口进行一个缩放矩阵和一个平移矩阵,来确保我们的视口中心点在屏幕中心点,我们视口的宽高和屏幕的宽高一致,这个就是视口变换。