刷题训练之前缀和-编程知识

> 作者：დ旧言~
> 座右铭：松树千年终是朽，槿花一日自为荣。

> 目标：熟练掌握前缀和算法。

> 毒鸡汤：学习，学习，再学习 ! 学，然后知不足。

> 专栏选自：刷题训练营

> 望小伙伴们点赞👍收藏✨加关注哟💕💕

🌟前言分析

最早博主续写了牛客网130道题，这块的刷题是让同学们快速进入C语言，而我们学习c++已经有一段时间了，知识储备已经足够了但缺少了实战，面对这块短板博主续写刷题训练，针对性学习，把相似的题目归类，系统的刷题，而我们刷题的官网可以参考：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

牛客网 - 找工作神器|笔试题库|面试经验|实习招聘内推，求职就业一站解决_牛客网

⭐知识讲解

前缀和只是一个算法的总称，其实前缀和可以分为前缀和，前缀积，这类算法更像是高中我们所学的数列的求和，寻找一组数列的规律，从而计算前缀和，这类题目很有规律的，学会画图，掌握题目的所隐藏的规律，这类题目就自然而然的可以解出。

⭐经典题型

🌙topic-->1

题目链接：1.前缀和

题目分析：

输入 n 个数字 ,求 q 次前缀和，这个 q 次前缀和范围在 l ~ r 之间（不是数组的下标，而是数组第l 的数），输出多组数据。

算法原理：

解法一：

暴力遍历数组，时间复杂度为O(n * q)，这个解法会超时，所以我们不用这个算法。

解法二：

采用前缀和的算法原理：

代码演示：

#include <iostream>
using namespace std;const int N = 100001; // 数据大小
long long arr[N],dp[N];
int n,q; int main() 
{// 输入cin >> n >> q;// 存入数据for(int i = 1;i <= n;i++)cin >> arr[i];// 前缀和for(int i = 1;i <= n;i++)dp[i] = dp[i - 1] + arr[i];// 输出while(q--){int l,r = 0;cin >> l >> r;// 计算前缀和cout << dp[r] - dp[l - 1] << endl;}return 0;
}

🌙topic-->2

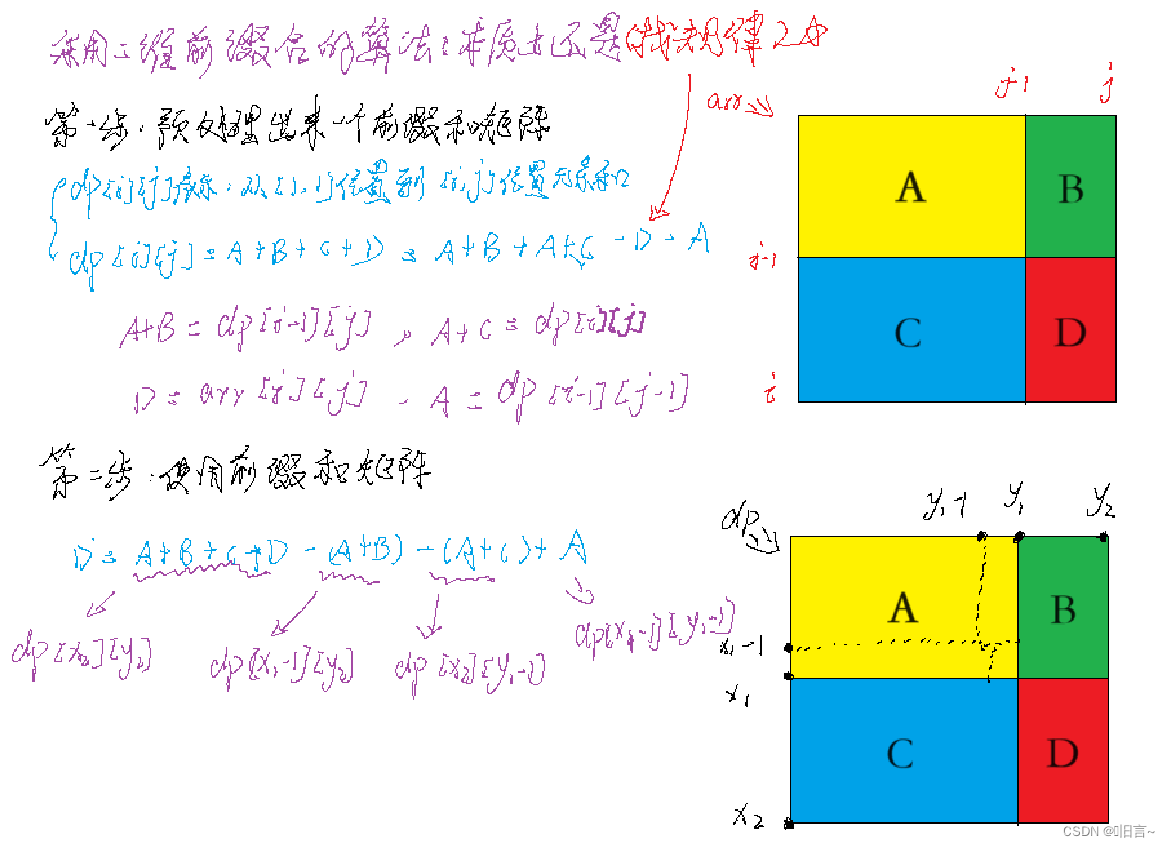
题目链接：2二维前缀和

题目分析：

在一个二维数组（ n * m）中，求 q 次二维前缀和，其中需要输入两个二维坐标，求输入这个两个坐标矩阵的和。

算法原理：

解法一：

暴力遍历二维数组，时间复杂度为O(n * m * q)，这个解法会超时，所以我们不用这个算法。

解法二：

采用二维前缀和的算法原理：

代码演示：

#include <iostream>
using namespace std;const int N = 1001; // 数据大小
int arr[N][N];
long long dp[N][N];
int n,m,q = 0;int main() 
{// 输入cin >> n >> m >> q;// 读入数据for(int i = 1 ;i <= n;i++)for(int j = 1;j <= m;j++)cin >> arr[i][j];// 处理数据for(int i = 1;i <=n;i++)for(int j = 1;j <= m;j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];// 使用前缀和矩阵int x1,y1,x2,y2 = 0;while(q--){cin >> x1 >> y1 >> x2 >> y2;// 采用公式cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 -1][y1 - 1] << endl;}return 0;
}

🌙topic-->3

题目链接：3.前缀和

题目分析：

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

算法原理：

解法一：

暴力遍历一维数组，这个解法会超时，所以我们不用这个算法。

解法二：

采用一维前缀和的算法原理：

代码演示：

class Solution {
public:int pivotIndex(vector<int>& nums) {// lsum[i] 表⽰：[0, i - 1] 区间所有元素的和// rsum[i] 表⽰：[i + 1, n - 1] 区间所有元素的和int n = nums.size();vector<int> lsum(n), rsum(n);// 预处理前缀和后缀和数组for (int i = 1; i < n; i++)lsum[i] = lsum[i - 1] + nums[i - 1];for (int i = n - 2; i >= 0; i--)rsum[i] = rsum[i + 1] + nums[i + 1];// 判断for (int i = 0; i < n; i++)if (lsum[i] == rsum[i])return i;return -1;}
};

🌙topic-->4

题目链接：4.前缀和

题目分析：

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

算法原理：

解法一：

暴力遍历一维数组，这个解法会超时，所以我们不用这个算法。

解法二：

采用一维前缀积的算法原理：

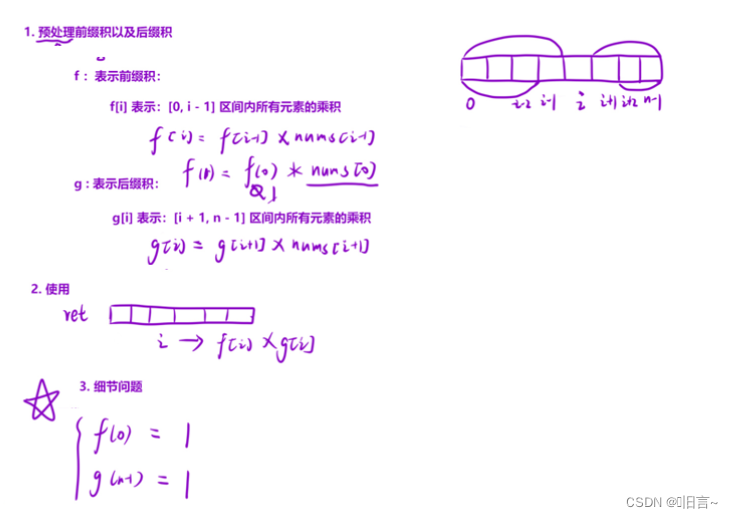
代码演示：

class Solution
{
public:vector<int> productExceptSelf(vector<int>& nums){// lprod 表⽰：[0, i - 1] 区间内所有元素的乘积// rprod 表⽰：[i + 1, n - 1] 区间内所有元素的乘积int n = nums.size();vector<int> lprod(n + 1), rprod(n + 1);lprod[0] = 1, rprod[n - 1] = 1;// 预处理前缀积以及后缀积for (int i = 1; i < n; i++)lprod[i] = lprod[i - 1] * nums[i - 1];for (int i = n - 2; i >= 0; i--)rprod[i] = rprod[i + 1] * nums[i + 1];// 处理结果数组vector<int> ret(n);for (int i = 0; i < n; i++)ret[i] = lprod[i] * rprod[i];return ret;}
};

🌙topic-->5

题目链接：5.前缀和

题目分析：

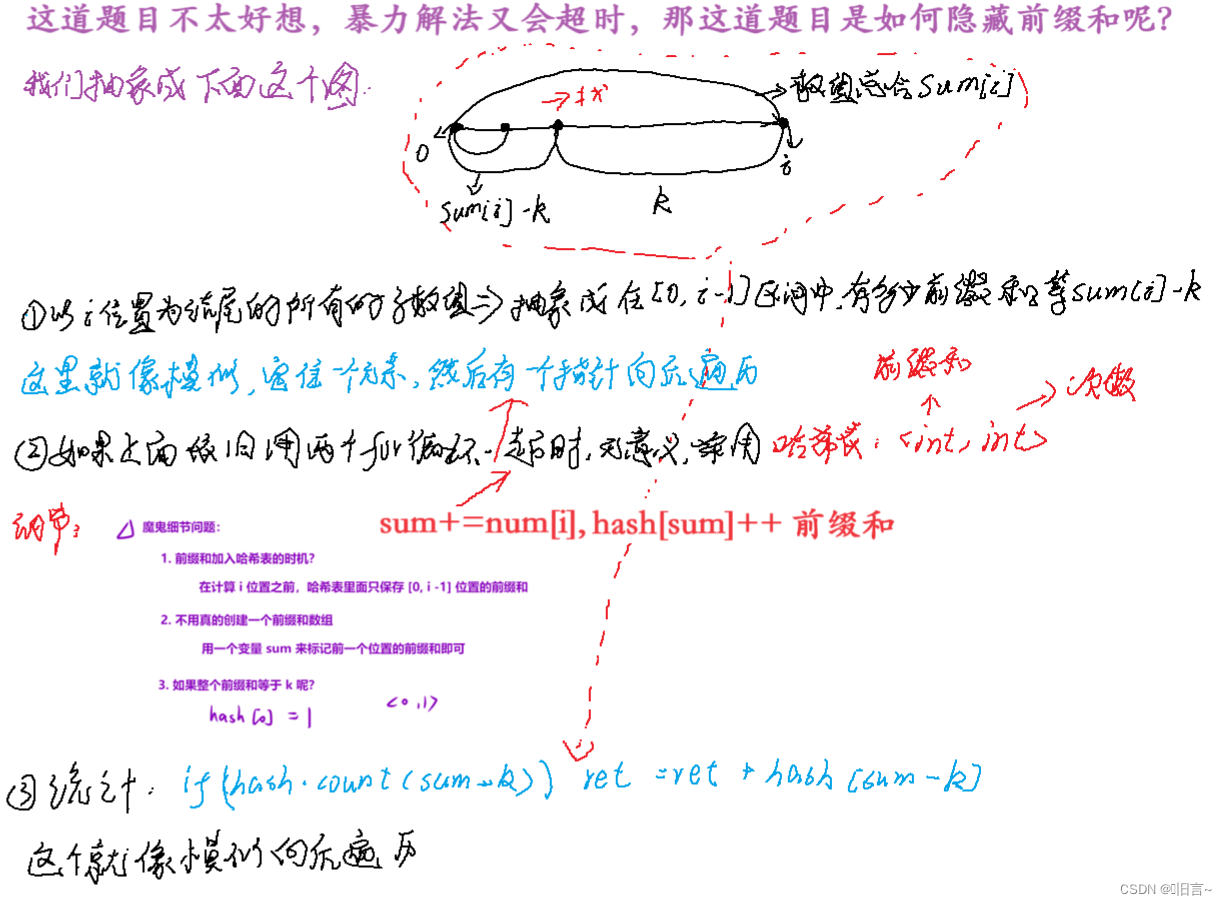
给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。子数组是数组中元素的连续非空序列。

算法原理：

解法一：

暴力遍历一维数组，定住一个元素向后寻找，时间复杂度为 O(n*n) ，这个解法会超时，所以我们不用这个算法。

解法二：

采用一维前缀和的算法原理：

代码演示：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int> hash;// 统计前缀和出现的个数hash[0] = 1;// 处理边界问题int sum = 0,ret = 0;// 循环for(auto x : nums){sum = sum + x;// 累计起来if(hash.count(sum - k)) // 模拟指针向后移ret = ret + hash[sum - k];hash[sum]++;}return ret;}
};

🌙topic-->6

题目链接：6.前缀和

题目分析：

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的（连续、非空） 子数组 的数目。

子数组 是数组的连续部分。

算法原理：

解法一：

暴力遍历一维数组，定住一个元素向后寻找，时间复杂度为 O(n*n) ，这个解法会超时，所以我们不用这个算法。

解法二：

采用一维前缀和的算法原理：

代码演示：

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k){unordered_map<int, int> hash;hash[0 % k] = 1; // 0 这个数的余数int sum = 0, ret = 0;for (auto x : nums){sum += x; // 算出当前位置的前缀和int r = (sum % k + k) % k; // 修正后的余数if (hash.count(r)) ret += hash[r]; // 统计结果hash[r]++;}return ret;}
};

🌙topic-->7

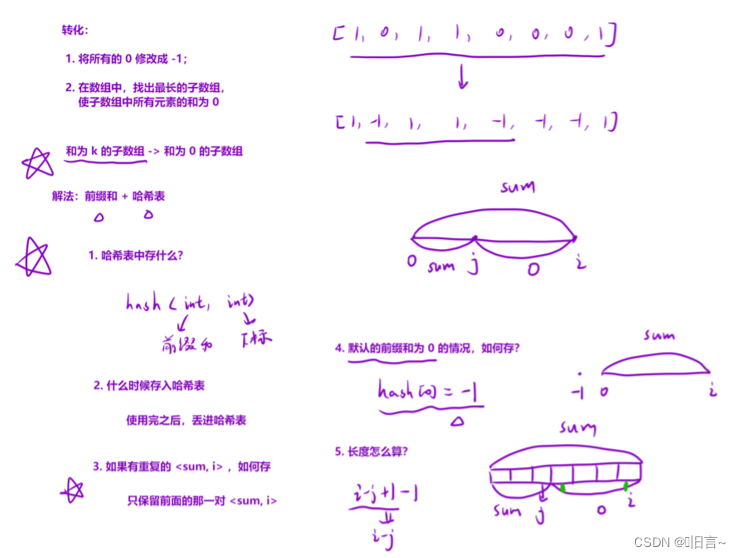
题目链接：7.前缀和

题目分析：

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

nums[i] 不是 0 就是 1

算法原理：

解法一：

暴力遍历一维数组，定住一个元素向后寻找，时间复杂度为 O(n*n) ，这个解法会超时，所以我们不用这个算法。

解法二：

采用一维前缀和的算法原理：

代码演示：

class Solution
{
public:int findMaxLength(vector<int>& nums){unordered_map<int, int> hash;hash[0] = -1; // 默认有⼀个前缀和为 0 的情况int sum = 0, ret = 0;for (int i = 0; i < nums.size(); i++){sum += nums[i] == 0 ? -1 : 1; // 计算当前位置的前缀和if (hash.count(sum)) ret = max(ret, i - hash[sum]);else hash[sum] = i;}return ret;}
};

🌙topic-->8

题目链接：8.前缀和

题目分析：

给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和。

算法原理：

解法一：

暴力遍历二维数组，定住一个元素向后寻找，时间复杂度为 O(n*n) ，这个解法会超时，所以我们不用这个算法。

解法二：

采用二维前缀和的算法原理：（和第二题相似）

代码演示：

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));// 1. 预处理前缀和矩阵for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] +mat[i - 1][j - 1];// 2. 使⽤vector<vector<int>> ret(m, vector<int>(n));for (int i = 0; i < m; i++)for (int j = 0; j < n; j++){int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +dp[x1 - 1][y1 - 1];}return ret;}
};