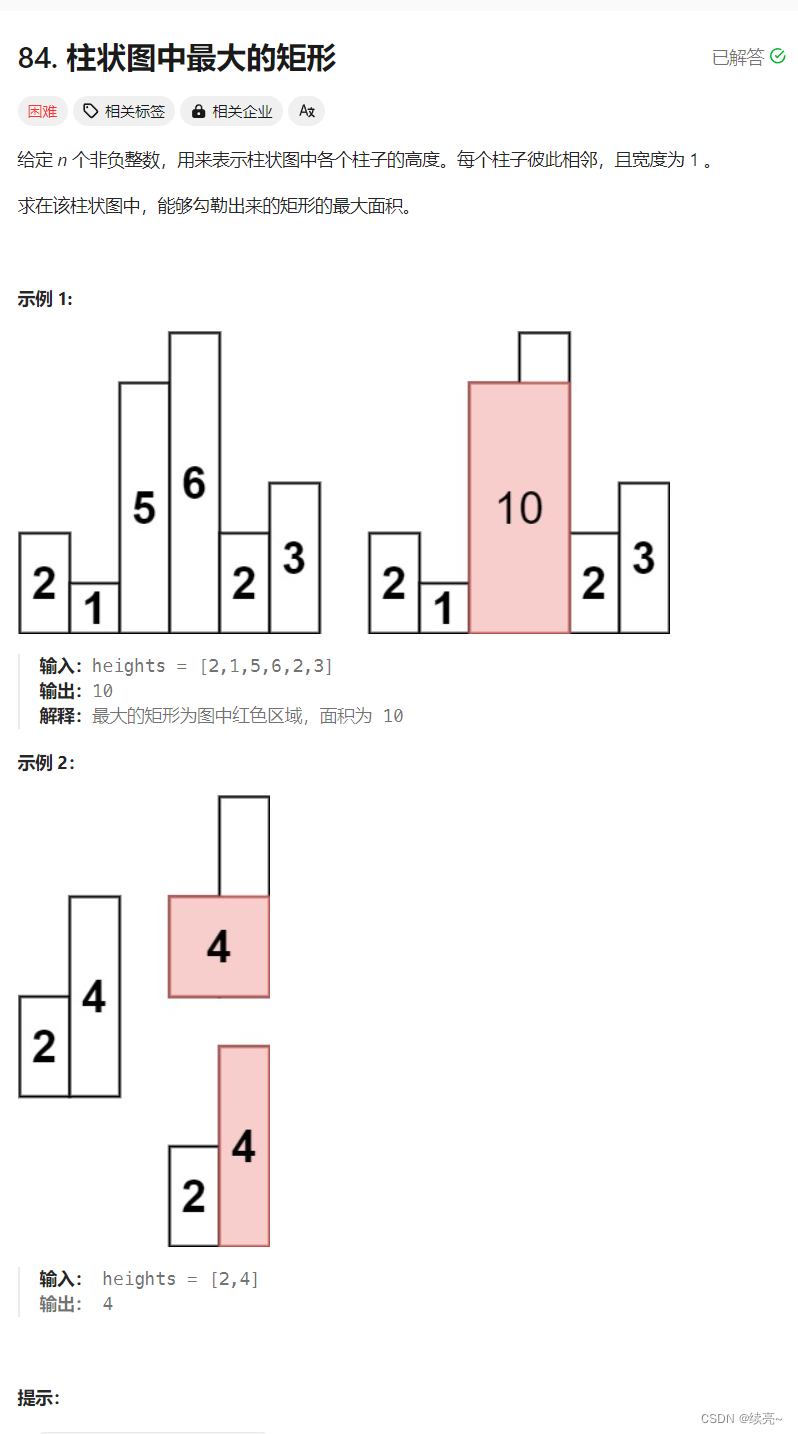
思路:
矩形面积:宽度*高度
高度如何确定呢?就是在宽度中最矮的元素。如何确定宽度,就是要确定左右边界。
当我们在处理直方图最大矩形面积问题时,遇到一个比栈顶柱子矮的新柱子时开始计算面积的原因关键在于如何确定一个矩形的左右边界:
-
左边界的确定:
- 在单调递增栈中,每一个柱子的左边界是由前一个比它矮的柱子决定的。当一个柱子入栈时,栈中前一个柱子的高度必定小于或等于当前柱子的高度。因此,当某个柱子被从栈中弹出时,意味着找到了一个比它高的左边界,这个左边界正是栈中该柱子前面的柱子的位置。
-
右边界的确定:
- 当我们遇到一个比栈顶柱子矮的新柱子时,这个新柱子的索引就成了栈顶柱子的右边界,因为这标志着右侧出现了一个无法继续扩展当前栈顶柱子宽度的点。此时,栈顶柱子及其之前的所有比它高的柱子都需要被处理,因为我们已经找到了它们的右边界。
-
面积计算:
- 弹出栈顶元素(某个高柱子),此时可以确定该柱子的高度,而宽度是从它的左边界(前一个栈元素,如果栈为空则为-1)到右边界(当前低柱子的前一个位置)之间的距离。计算出的面积就是以该高柱子为高的最大矩形面积。
代码如下:
class Solution {public int largestRectangleArea(int[] heights) {int n = heights.length; // 直方图的柱子个数Stack<Integer> stack = new Stack<>(); // 使用栈来存储柱子的索引int res = 0; // 最大面积初始化为0// 遍历每个柱子for (int i = 0; i < n; i++) {// 当栈不为空,并且当前柱子的高度小于栈顶柱子的高度时while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {int height = heights[stack.pop()]; // 获取栈顶柱子的高度int width = 0; // 初始化宽度// 如果栈为空,说明当前弹出的柱子左边没有比它矮的柱子if (stack.isEmpty()) {width = i; // 宽度为当前索引} else {// 否则,宽度为当前索引减去新的栈顶索引减一width = i - stack.peek() - 1;}// 计算可能的最大面积,并更新结果res = Math.max(res, width * height);}// 将当前柱子的索引入栈stack.push(i);}// 清理栈中剩余的柱子while (!stack.isEmpty()) {int height = heights[stack.pop()]; // 获取栈顶柱子的高度int width = 0; // 初始化宽度// 如果栈为空,说明右边没有柱子if (stack.isEmpty()) {width = n; // 宽度为柱子总数} else {// 否则,宽度为柱子总数减去新的栈顶索引减一width = n - stack.peek() - 1;}// 计算可能的最大面积,并更新结果res = Math.max(res, width * height); }return res; // 返回最大面积}
}