前言
乘法器是Xilinx的数学运算IP核中最基础的IP核之一,熟练掌握它是使用FPGA进行数字信号处理的基础。
本文参考pg108-mult-gen.pdf——Multiplier v12.0。
一. IP 概述 与 产品手册
参考:[Multiplier (xilinx.com))](https://china.xilinx.com/products/intellectual-property/multiplier.html)

二. IP框图与信号端口
2.1 IP框图

2.2 端口信号列表
| 分类 | 名称 | 方向 | 必须/可选 | 位宽 | 说明 |
|---|---|---|---|---|---|
| 时钟与复位 | CLK | I | 必须 | 1 | 模块工作时钟,上升沿有效 |
| CE | I | 可选 | 1 | 时钟使能信号,高电平有效 | |
| SCLR | I | 可选 | 1 | 高电平同步清零,保持一个CLK周期的高电平则清零IP内所有寄存器(SCLR/CE优先级可配置) | |
| 输入 | A | I | 必须 | 1~64 | 乘法操作数A,可选有符号整数/无符号整数 |
| B | I | 可选 | 1~64 | 乘法操作数B,可选有符号整数/无符号整数,可为常量,此时无需输入(仅限并行乘法器) | |
| 输出 | P | O | 必须 | 2~128 | 乘积P,位宽为乘数位宽之和 |
三. IP使用配置
3.1 Basic(基本)选项卡
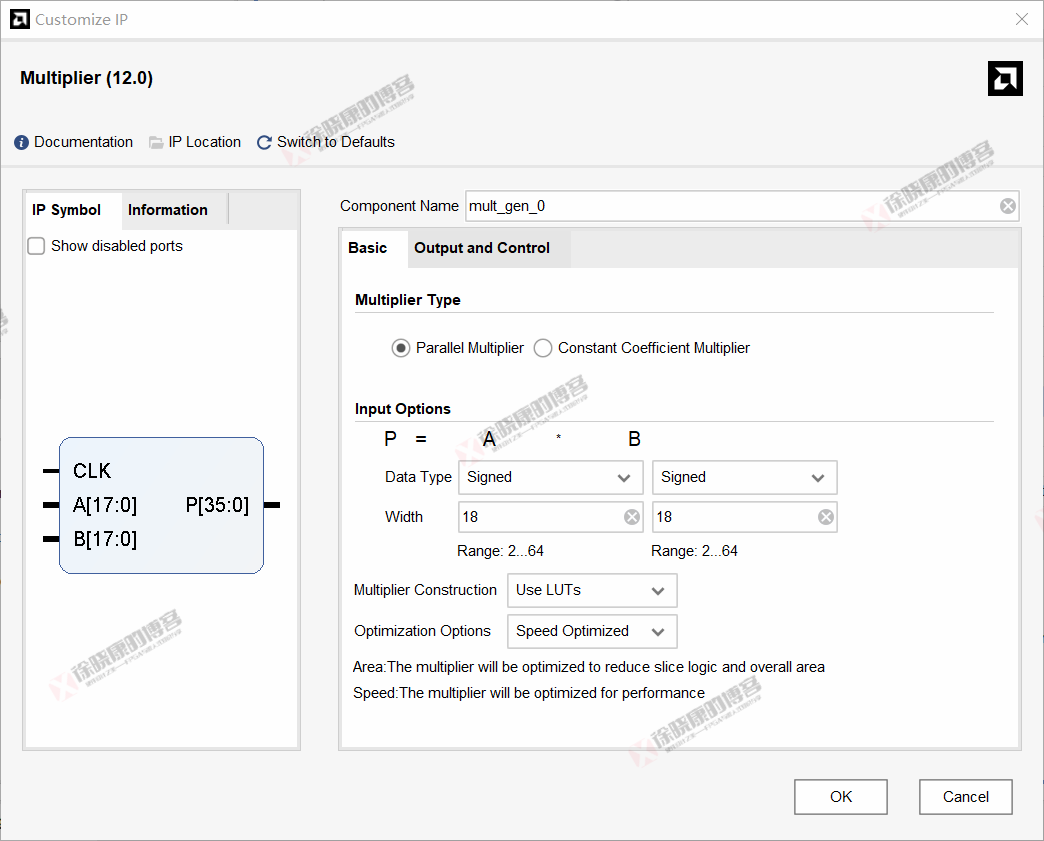
Mutiplier Type(乘法器类型)
Parallel Multiplier:并行乘法器,此时A,B都需要外部输入。
Constant Coeficient Multiplier,常系数乘法器,此时B为常数,仅A需要外部输入。
Input Options(输入选项)
有符号数位宽为2 ~ 64;无符号数位宽为1 ~ 64。
Multiplier Construction(乘法器构造)
Use LUTs:使用查找表构建乘法器。
Use Mults:使用FPGA嵌入的乘法器硬核构建乘法器。
Optimization Options(优化选项)
Speed Optimized:速度优化。
Area Optimized:面积优化。
- DSP48E1切片:对于乘法器尺寸不超过47x47的情况,可以选择速度优化或面积优化。速度优化充分利用乘法器原语,提供最高性能的实现。面积优化则结合使用片上逻辑和专用乘法器原语,以降低基于DSP切片的乘法器利用率,同时仍能保持合理的性能。对于尺寸超过47x47的乘法器,仅允许进行速度优化。
- 基于LUT的乘法器:面积优化可以在牺牲可实现时钟频率的前提下减少延迟和LUT利用率。当两个输入操作数均为无符号数且大小均小于16位时,面积优化效果最为显著。
3.2 Output and Control(输出与控制)选项卡
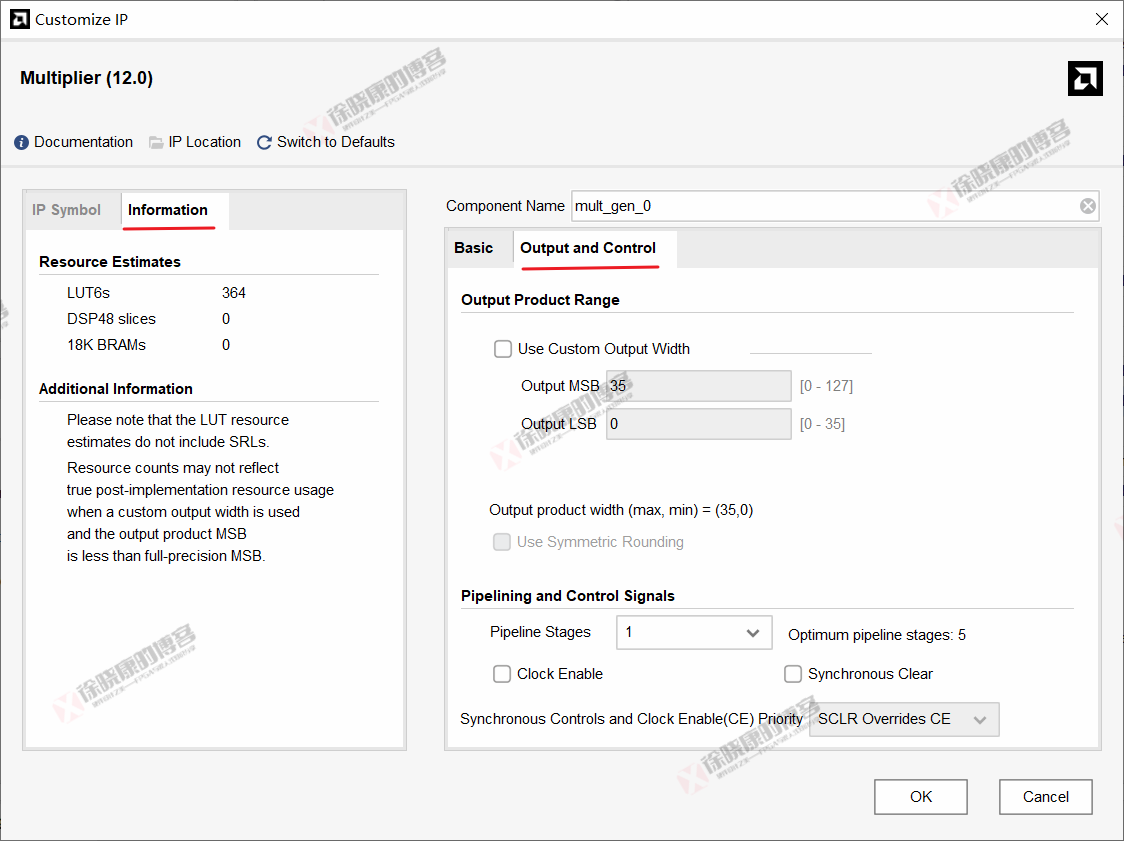
Output Product Range(输出乘积范围)
- Use Custom Output Width(使用自定义输出宽度):如果应用程序只需要乘积的一部分,可以通过设置MSB(最高有效位)和LSB(最低有效位)范围来自定义乘积位数。
- Use Symmetric Rounding(使用对称舍入):对于基于DSP切片的并行乘法器,如果需要,乘积可以对称地朝无穷大方向进行舍入。此行为与MATLAB®软件中的round函数相同。乘法器必须恰好占用一个DSP切片,且乘积的LSB(最低有效位)必须位于全范围乘积宽度之内。
Pipelining and Control Signals(流水线及控制信号)
Pipeline Stages (流水线级数):选择流水线级数。
Optimum pipeline stages(最优流水线级数):乘法器最大性能所需最优流水线级数。
IP假设所有输入都有寄存器。
- 流水线级数 = 0 意味着IP是组合逻辑的。
- 流水线级数 = 1 意味着只有IP输出有寄存器。
- 当流水线级数 > 1 时,将在输入和输出之间插入寄存器,直至达到最优流水线级数值。添加更多寄存器可以提高可实现的时钟速度,但会增加延迟。
- 将流水线级数设置为大于最优值的值将使IP完全流水化,并在输出处添加基于SRL16的移位寄存器以实现额外的延迟。
Clock Enable(时钟使能):选择设计中的所有寄存器是否具有时钟使能控制。
Synchronous Clear(同步清零):选择设计中的所有寄存器是否具有同步复位控制。
SCLR/CE 优先级:当SCLR和CE引脚同时存在时,可以选定SCLR和CE的优先级。当SCLR优先于CE时,将使用最少的资源并实现最佳性能。
3.3 Information(信息)
上图左侧的信息窗口,可以看到用到的LUT6、DSP48片 和 18K BRAM的数量。
四. IP使用注意事项与仿真
在以下模块中,实例化了乘法器IP,并定义了直接用乘法符号*的乘法,比较IP结果和直接符号结果是否一样。
module TryMult
#(parameter A_WIDTH = 18,parameter B_WIDTH = 18
)(input wire signed [A_WIDTH-1 : 0] a,input wire signed [B_WIDTH-1 : 0] b,output wire signed [A_WIDTH+B_WIDTH-1 : 0] p,output wire signed [A_WIDTH+B_WIDTH-1 : 0] p_comb,output reg signed [A_WIDTH+B_WIDTH-1 : 0] p_r1,// input wire ce,// input wire sclr,input wire clk
);// 直接用*与用IP效果一样
assign p_comb = a * b;always @(posedge clk) beginp_r1 <= a * b;
endmult_gen_0 mult_gen_0_u0 (// .CLK (clk ), // input wire CLK.A (a ), // input wire [17: 0] A.B (b ), // input wire [17: 0] B// .CE (ce ), // input wire CE// .SCLR (sclr), // input wire SCLR.P (p )// output wire [35: 0] P
);endmodule
testbench部分代码如下:
// 生成时钟
localparam CLKT = 2;
initial beginclk = 0;forever #(CLKT / 2) clk = ~clk;
endlocalparam N = 16;
logic [A_WIDTH-1 : 0] a_ls [N] = {'h0, 'h1, 'h2, 'h3, 'h4, 'h5, 'h6, 'h7, 'h8, 'h9, 'hA, 'hB, 'hC, 'hD, 'hE, 'hF};
logic [B_WIDTH-1 : 0] b_ls [N] = {'h0, 'h1, 'h2, 'h3, 'h4, 'h5, 'h6, 'h7, 'h8, 'h9, 'hA, 'hB, 'hC, 'hD, 'hE, 'hF};initial begin#(CLKT * 2.6)for (int i = 0; i < N; i++) begina = a_ls[i];b = b_ls[i];#(CLKT * 1);end#(CLKT * 2)$stop;
end
下面根据想验证的问题分别进行仿真。
4.1 乘法器输入到输出间的延时
即从输入数据有效,时钟有效,到输出数据有效间的时延是多少?是固定的还是和IP设置中的流水线级数(Pipeline Stages)有关?
仿真条件1:流水线级数 = 0,此时乘法器为组合逻辑,无clk。从下图可见,乘法器输出P没有延迟,完全跟随输入变化而变化,且与组合逻辑中直接用乘号*结果一样。
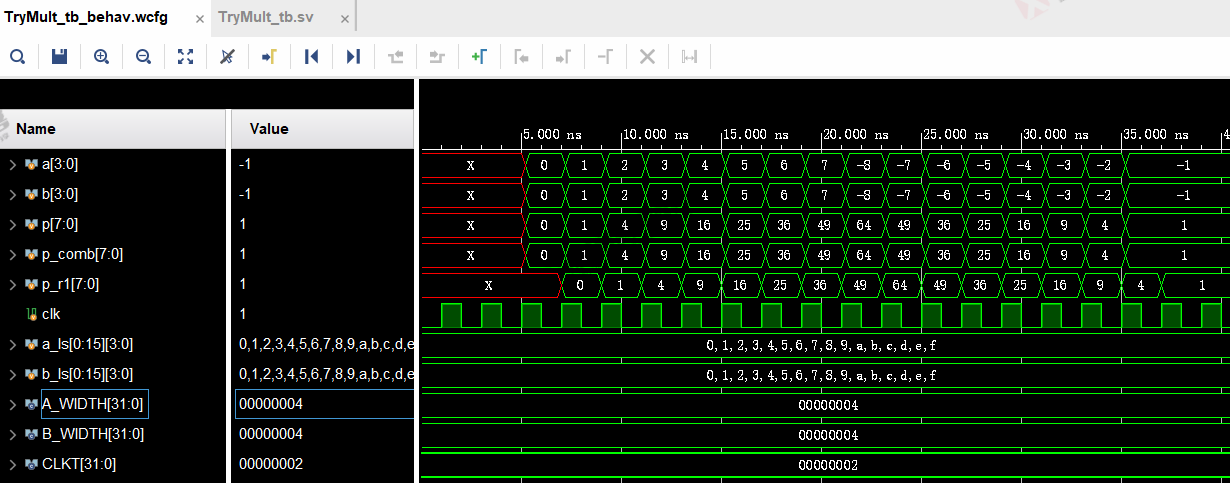
仿真条件2:流水线级数 = 1,此时乘法器输出有一个寄存器,有clk。从下图可见输出P延迟为1个clk周期,与在时序逻辑中使用乘号*结果一样。
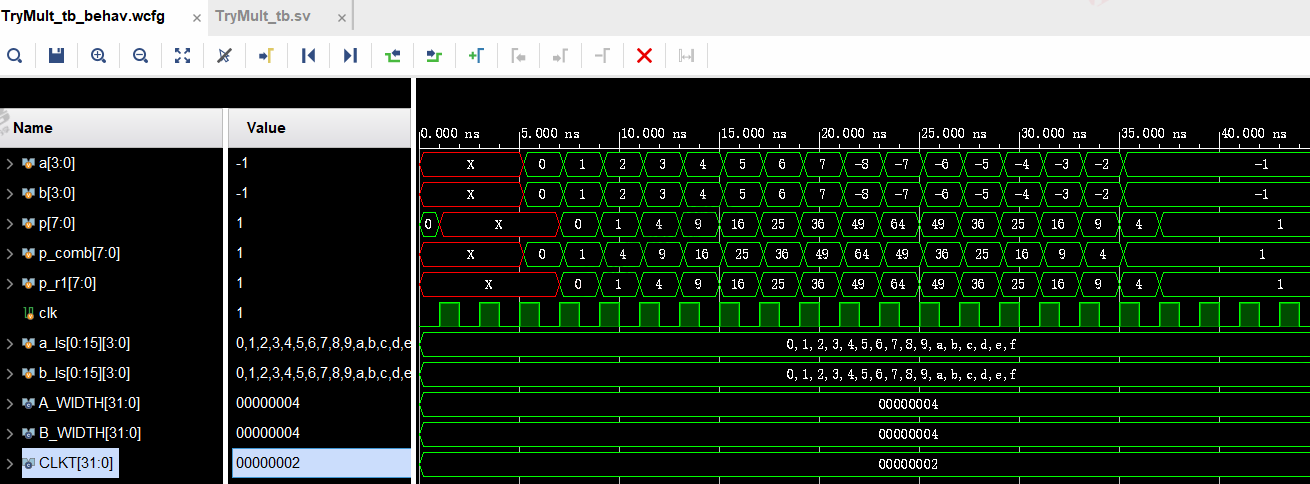
仿真条件3:流水线级数=3,此时延迟3个clk周期。
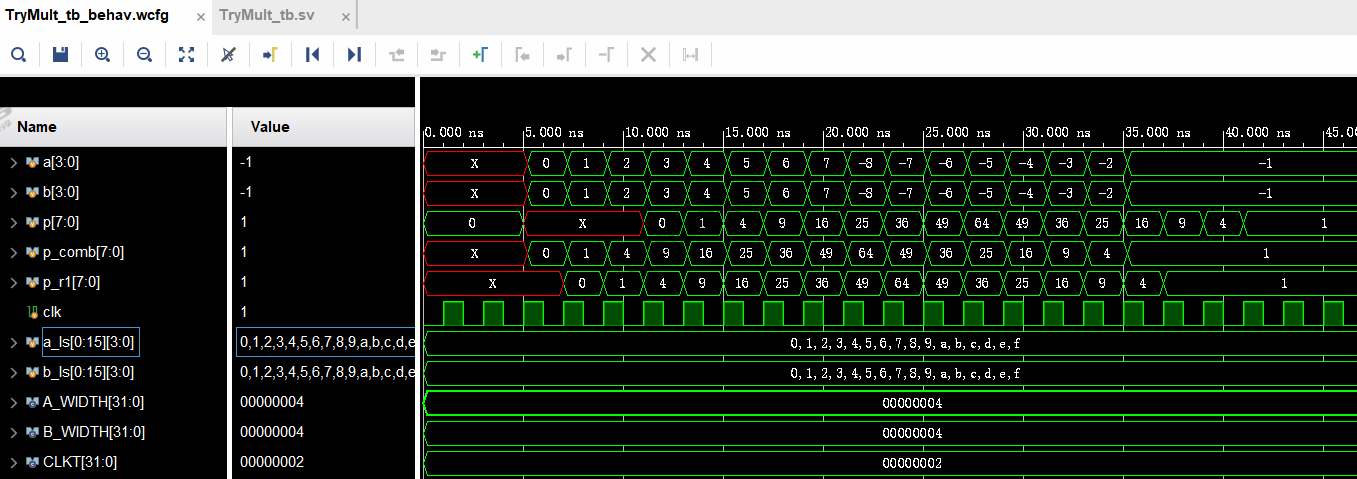
结论:延时完全由IP设置中的流水线级数决定,延迟周期数就等于流水线级数。
4.2 输出位宽与输入位宽的关系
假定条件:乘数A,位宽N;乘数B,位宽M,这里假定M≥N。乘法器的IP输出乘积的位宽总是被设定为两个乘数的位宽之和,所以乘积P位宽为N+M。
这部分的分析是为了弄清楚:什么情况下,乘积的位宽可以减小1位,即用N+M-1位也可以完全表示乘积。
乘法器的输入按是否有符号可以分为以下三类,分别说明。
-
无符号数×无符号数
-
无符号数×有符号数
-
有符号数×有符号数
4.2.1 无符号数×无符号数
A ∈ [ 0 , 2 N − 1 ] , N ⩾ 1 B ∈ [ 0 , 2 M − 1 ] , M ⩾ N ( 2 N − 1 ) ( 2 M − 1 ) = 2 N + M − 2 N − 2 M + 1 A × B = [ 0 , 2 N + M − 2 N − 2 M + 1 ] P ∈ [ 0 , 2 N + M ] 可完全包含 A × B A\in \left[ 0, 2^N-1 \right] \text{,}N\geqslant 1 \\ B\in \left[ 0, 2^M-1 \right] \text{,}M\geqslant N \\ \left( 2^N-1 \right) \left( 2^M-1 \right) =2^{N+M}-2^N-2^M+1 \\ A\times B=\left[ 0, 2^{N+M}-2^N-2^M+1 \right] \\ P\in \left[ 0, 2^{N+M} \right] \text{可完全包含}A\times B A∈[0,2N−1],N⩾1B∈[0,2M−1],M⩾N(2N−1)(2M−1)=2N+M−2N−2M+1A×B=[0,2N+M−2N−2M+1]P∈[0,2N+M]可完全包含A×B
设想P减小1位,此时 P ∈ [ 0 , 2 N + M − 1 ] P\in \left[ 0, 2^{N+M-1} \right] P∈[0,2N+M−1],有:
Δ = 2 N + M − 1 − ( 2 N + M − 2 N − 2 M + 1 ) = 2 N + 2 M − 2 N + M − 1 − 1 \varDelta =2^{N+M-1}-\left( 2^{N+M}-2^N-2^M+1 \right) =2^N+2^M-2^{N+M-1}-1 Δ=2N+M−1−(2N+M−2N−2M+1)=2N+2M−2N+M−1−1
如果N=1,则 Δ = 2 + 2 M − 2 M − 1 = 1 > 0 \varDelta =2+2^M-2^M-1=1>0 Δ=2+2M−2M−1=1>0总是成立。
如果N=2,则 Δ = 4 + 2 M − 2 ∗ 2 M − 1 = 3 − 2 M > 0 \varDelta =4+2^M-2*2^M-1=3-2^M>0 Δ=4+2M−2∗2M−1=3−2M>0,而 M ⩾ N M\geqslant N M⩾N,此式总是不成立。
考虑到,乘数位宽为1时通常不需要用到乘法器。
结论:无法缩减位宽,乘积位宽等于两乘数位宽之和。
4.2.2 无符号数×有符号数
A ∈ [ 0 , 2 N − 1 ] , N ⩾ 1 B ∈ [ − 2 M − 1 , 2 M − 1 − 1 ] , M ⩾ 2 A × B = [ − 2 N + M − 1 + 2 M − 1 , 2 N + M − 1 − 2 N − 2 M − 1 + 1 ] P ∈ [ − 2 N + M − 1 , 2 N + M − 1 − 1 ] 可完全包含 A × B A\in \left[ 0, 2^N-1 \right] \text{,}N\geqslant 1 \\ B\in \left[ -2^{M-1}, 2^{M-1}-1 \right] \text{,}M\geqslant 2 \\ A\times B=\left[ -2^{N+M-1}+2^{M-1}, 2^{N+M-1}-2^N-2^{M-1}+1 \right] \\ P\in \left[ -2^{N+M-1}, 2^{N+M-1}-1 \right] \text{可完全包含}A\times B A∈[0,2N−1],N⩾1B∈[−2M−1,2M−1−1],M⩾2A×B=[−2N+M−1+2M−1,2N+M−1−2N−2M−1+1]P∈[−2N+M−1,2N+M−1−1]可完全包含A×B
设想P减小1位,此时 P ∈ [ − 2 N + M − 2 , 2 N + M − 2 − 1 ] P\in \left[ -2^{N+M-2}, 2^{N+M-2}-1 \right] P∈[−2N+M−2,2N+M−2−1],考虑P的最小值与A×B最小值的差值:
Δ 左 = − 2 N + M − 2 + 2 N + M − 1 − 2 M − 1 = 2 M − 1 ( 2 N − 1 − 1 ) ⩽ 0 仅对 N = 1 成立 \varDelta _{\text{左}}=-2^{N+M-2}+2^{N+M-1}-2^{M-1}=2^{M-1}\left( 2^{N-1}-1 \right) \leqslant 0 \\\text{仅对}N=1\text{成立} Δ左=−2N+M−2+2N+M−1−2M−1=2M−1(2N−1−1)⩽0仅对N=1成立
所以,P直接缩小1位不行,无法包含所有乘积的值。
继续考虑以下情况,二进制补码的最小值是比较特殊的,有符号数的M很大,考虑去掉这个最小值类似[10000],用次小值类似[10001]替代,再看乘积范围,有:
B ∈ [ − 2 M − 1 + 1 , 2 M − 1 − 1 ] , M ⩾ 3 A × B = [ ( 2 N − 1 ) ( − 2 M − 1 + 1 ) , ( 2 N − 1 ) ( 2 M − 1 − 1 ) ] Δ 左 = 2 M − 1 ( 2 N − 1 − 1 ) − 2 ( 2 N − 1 − 1 ) − 1 = ( 2 M − 1 − 2 ) ( 2 N − 1 − 1 ) − 1 ⩽ 0 上式仅对 N = 1 或 M = 2 成立 B\in \left[ -2^{M-1}+1, 2^{M-1}-1 \right] \text{,}M\geqslant 3 \\ A\times B=\left[ \left( 2^N-1 \right) \left( -2^{M-1}+1 \right) , \left( 2^N-1 \right) \left( 2^{M-1}-1 \right) \right] \\ \varDelta _{\text{左}}=2^{M-1}\left( 2^{N-1}-1 \right) -2\left( 2^{N-1}-1 \right) -1=\left( 2^{M-1}-2 \right) \left( 2^{N-1}-1 \right) -1\leqslant 0 \\ \text{上式仅对}N=1\text{或}M=2\text{成立} B∈[−2M−1+1,2M−1−1],M⩾3A×B=[(2N−1)(−2M−1+1),(2N−1)(2M−1−1)]Δ左=2M−1(2N−1−1)−2(2N−1−1)−1=(2M−1−2)(2N−1−1)−1⩽0上式仅对N=1或M=2成立
这就没什么实际意义了,所以去掉有符号数的最小值也无法令乘积减小一位位宽。
结论:无法缩减位宽,乘积位宽等于两乘数位宽之和。
4.2.3 有符号数×有符号数
A ∈ [ − 2 N − 1 , 2 N − 1 − 1 ] , N ⩾ 2 B ∈ [ − 2 M − 1 , 2 M − 1 − 1 ] , M ⩾ N A × B = [ − 2 N + M − 2 + 2 N − 1 , 2 N + M − 2 ] P ∈ [ − 2 N + M − 1 , 2 N + M − 1 − 1 ] 可完全包含 A × B A\in \left[ -2^{N-1}, 2^{N-1}-1 \right] \text{,}N\geqslant 2 \\ B\in \left[ -2^{M-1}, 2^{M-1}-1 \right] \text{,}M\geqslant N \\ A\times B=\left[ -2^{N+M-2}+2^{N-1}, 2^{N+M-2} \right] \\ P\in \left[ -2^{N+M-1}, 2^{N+M-1}-1 \right] \text{可完全包含}A\times B A∈[−2N−1,2N−1−1],N⩾2B∈[−2M−1,2M−1−1],M⩾NA×B=[−2N+M−2+2N−1,2N+M−2]P∈[−2N+M−1,2N+M−1−1]可完全包含A×B
设想P减小一位,此时有:
P ∈ [ − 2 N + M − 2 , 2 N + M − 2 − 1 ] P\in \left[ -2^{N+M-2}, 2^{N+M-2}-1 \right] P∈[−2N+M−2,2N+M−2−1]
最小值可以覆盖,最大值差1。那么A×B的最大值何时取到呢?只有一种情况, A = − 2 N − 1 且 B = − 2 M − 1 A=-2^{N-1}\text{且}B=-2^{M-1} A=−2N−1且B=−2M−1。
结论:如果将其中一个乘数的最小值用次小值代替,那么就P减小一位也可完全包含A×B了。
当乘数位宽较大时,这是个不错的缩减乘积位宽的办法,误差很小。
补码最小值用次小值替代的示例Verilog代码如下:
module minTwoCompAddOne
#(parameter A_WIDTH = 18 // 乘数A的宽度 大于等于3
)(input wire signed [A_WIDTH-1 : 0] a,output reg signed [A_WIDTH-1 : 0] new_a
);always @(*) beginif (a[A_WIDTH-1] == 1 && (|a[A_WIDTH-2 : 0] == 0))new_a <= {a[A_WIDTH-1:1], 1'b1};elsenew_a <= a;
endendmodule
4.3 同步清零SCLR与时钟使能CE失效后,输出是什么?
仿真条件1:流水线级数=3,选中CE和SCLR,控制CE。
从下图可以看到,CE失效后,乘积P会保存前几次的有效输出,当CE有效后立即输出,注意输出p的1和4,而p=36是CE有效后,延迟3个周期后的正常输出,正常输出的优先级是最高的。
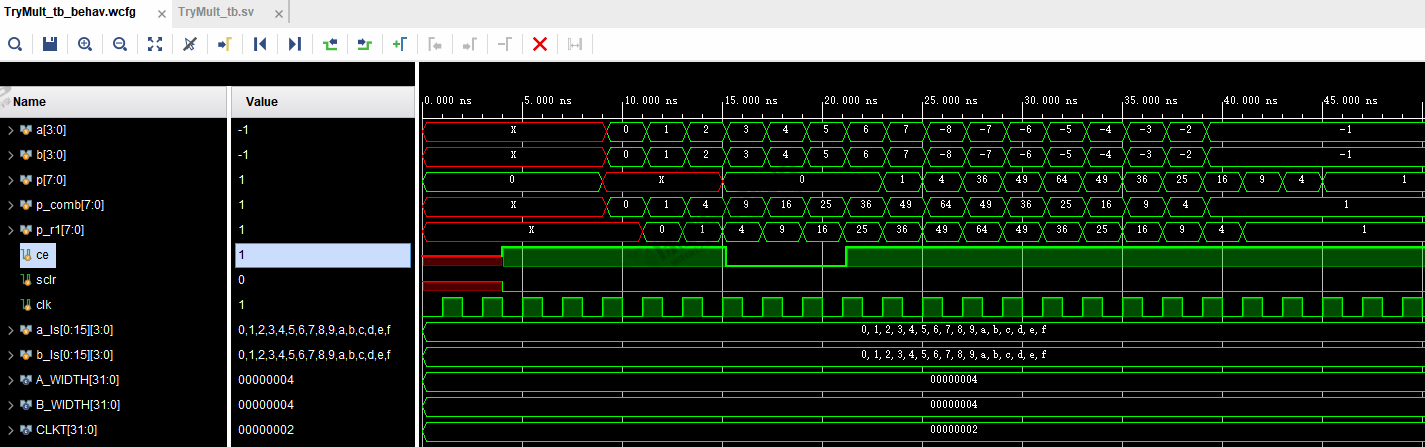
结论:CE有效时,乘法器存储输入乘数进行运算。当CE失效后,乘法器保持上一个有效输出;等CE再次有效后,继续进行之前输入乘数未完成的运算,直到新的输入延迟3个周期后正常输出。可见CE的作用是控制是否采用输入,以及暂停流水线。
仿真条件2:流水线级数=3,选中CE和SCLR,控制SCLR。
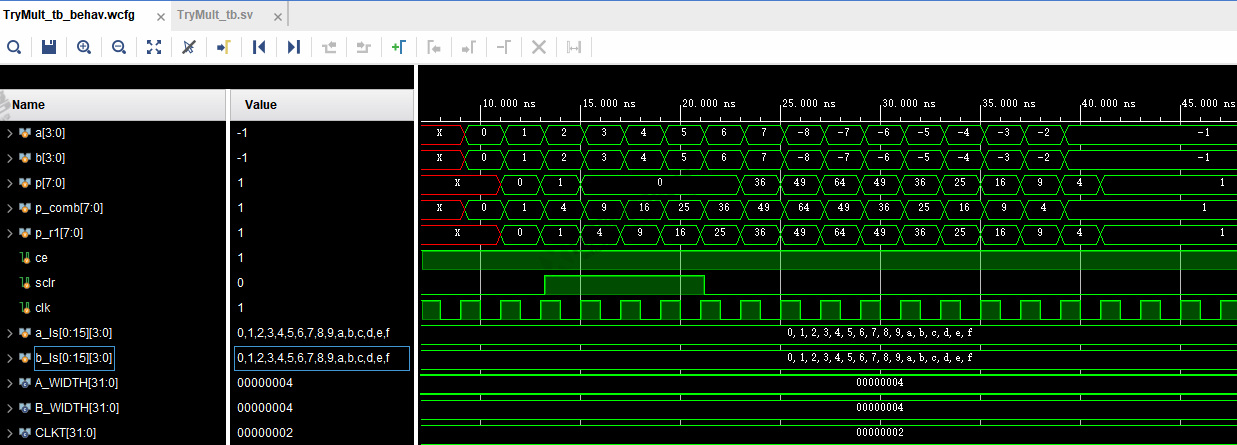
注意:SCLR有效后,输出立即清零;SCLR失效后,注意p=36,这是SCLR失效后的第一个正常输出,在正常输出之前,输出仍然是0,因为SCLR会将所有历史输出都清零。
结论:SCLR是所有寄存器清零,流水线的每一级都被清零了。
五. IP使用建议与工程分享
如果你不关注乘法器如何实现,不额外控制乘法器输入延时,则可以直接在代码中使用乘号*,而不需要使用乘法器IP。
Xilinx IP解析之Multiplier v12.0 Vivado2023.2工程.7z。
欢迎大家关注我的公众号:徐晓康的博客,回复以下四位数字获取。
3211
建议复制过去不会码错字!




![[二叉树] 二叉树的前中后三序遍历#知二求一](https://img-blog.csdnimg.cn/direct/3d2778545bd94326848801ecdde4aa75.png)