前言

提示：本份真诚面对自己、坦然无碍面对他人，就是优雅。

数组中的比较经典性问题:

单调数组问题
数组合并问题

单调数组问题

参考例子：896. 单调数列 - 力扣（LeetCode）
在这里插入图片描述

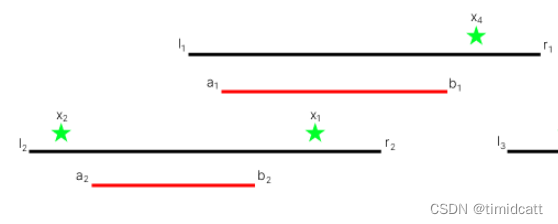
这里先思考一下：数组有序是前提，通过增/减两种状态，可以采用不同的策略。

对于所有的 i <= j 使得 a[i] <= a[j] 则说明数组 a 是单调递增的，反之，对所有的 i <= j ,使得所有的a[i] >= a[j],那么数组 a 是单调递增的。
所有遍历数组执行判断就可以解决，由于存在两种情况，我们需要两次循环就可以

展示代码🥰

 /*** 第一种方法，两次遍历确定，第一次确定是否递增 ，第二次** @param nums* @return*/public static boolean isMonotonic(int[] nums) {return isSorted(nums, true) || isSorted(nums, false);}public static boolean isSorted(int[] nums, boolean increasing) {int n = nums.length;for (int i = 0; i < n - 1; ++i) {if(increasing){ // 增 if (nums[i] > nums[i + 1]) {return false;}}else{if (nums[i] < nums[i + 1]) {return false;}}}return true;}

当然这样写是可以通过测试的，但是显得有点繁琐了😁，需要遍历两次，想一下这里需要怎么优化呢💡

我们关注一下 i 和 i + 1出现的位置 nums[i] > nums[i + 1]，而在另外的一个地方 j 和 j + 1 出现的位置nums[j] < num[j + 1]，那是不是说明就是单调的？这样的化我们可以使用两个变量标记一下，代码如下：

    /*** 第二种方式，一次遍历确定*如果是递增的就一定不能出现递减的相邻元素，* 如果出现递减的就一定不能出现递增的相邻元素。* @param nums* @return*/public static boolean isMonotonic_2(int[] nums) {boolean des = true, inc = true;int n = nums.length;for (int i = 0; i < n - 1; i++) {if (nums[i] > nums[i + 1]) {inc = false;}if (nums[i] < nums[i + 1]) {des = false;}}return des || inc;}

技巧：两元式结果的特殊处理，|| 运算的运用。

搜索插入位置：

数组单调性，是一个重要的信息，很多时候要将特定的元素插入到有序序列，并且保证插入后的顺序依然有序，比如力扣的 35 题：35. 搜索插入位置 - 力扣（LeetCode）

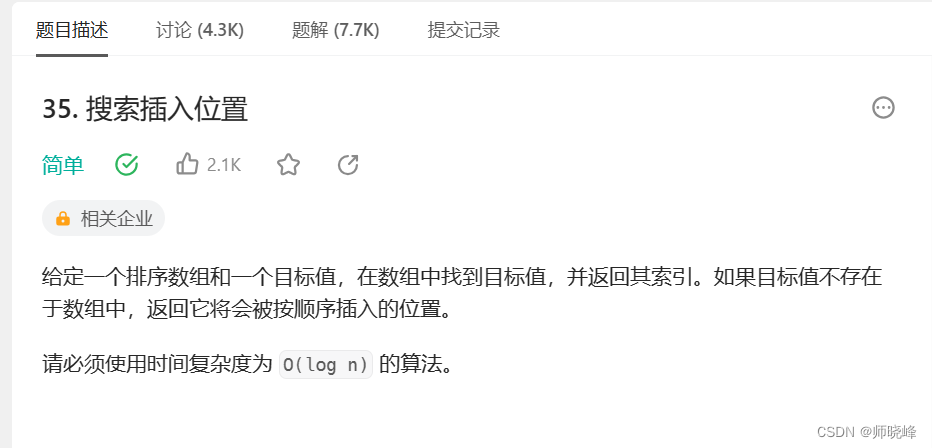
在这里插入图片描述

这个问题让我们将元素位置返回，比较简单，只需要遍历一边数组就可以找到答案。当然想这样的问题，如何快速的寻找目标元素，我们需要有二分的概念。以后但凡遇到单调序列中查找的情况，脑海中马上想到二分，迅速反应。

题解：

class Solution {public int searchInsert(int[] nums, int target) {int n = nums.length;for(int i = 0; i < n; i++){if(nums[i] >= target){return i;}}// 出现再最后一个return n;}
}

这里贴一下代码提供思考💡( 二分思想）

 public static int searchInsert(int[] nums, int target) {// 拿到 数组长度int n = nums.length;// 确定左右int left = 0, right = n - 1, ans = n;while(left <= right){// 思考这里问什么是 小于等于// 确定 中间值int mid = (right - left) / 2 + left;if (nums[mid] >= target){ans = mid;right = mid - 1;}else {left = mid + 1;}}return ans;}

数组合并问题：

数组合并是将两个或者多个有序数组合并成一个新的数组。当然这个问题本事不是很难，但是要写的出彩，确实需要花费一些功夫的，这个问题也是比较经典的问题。

先来看看力扣 88 题，88. 合并两个有序数组 - 力扣（LeetCode）
在这里插入图片描述
对于这个问题嘛，简单的思路就是

将nums2 添加在nums1 的后面
排序

/*** 方法1：先合并再排序实现排序** @param nums1 第一个数组* @param nums1_len 第一个数组的长度* @param nums2  第二个数组，将nums2合并到nums1中* @param nums2_len 第二个数组的长度*/public static void merge1(int[] nums1, int nums1_len, int[] nums2, int nums2_len) {for (int i = 0; i < nums2_len; i++) {nums1[nums1_len + i] = nums2[i];}Arrays.sort(nums1);}

当然这样写太没有技术含量了，面试官也不喜欢。这道题的关键是将nums2合并到nums1 中并且还要保证有序。因为nums1是数组不能强行插入。如果从前面向后面出插入，数组nums1后面的元素会多次移动，代价太高了。此时再借助一个数组就可以解决这个问题 ans，把选好的数组元素放入ans中，最后返回，很好的解决以上为题。

这样的化面试官会接着向下考察：可以优化一下，或者不申请数组。（专业的说法是，空间复杂度O(n),可以采用O(1)的方法实现？

比较好的方式从后向前插入，nums1 和 nums2 的元素是固定的，所以排序后最远位置一定是nums1 和 nums2 中最大的那一个，一次类推，每次找最大的，就可以实现从后向前填了，展示一下代码：

/*** 方法2：两个数组从后向前逐步合并** @param nums1* @param nums1_len* @param nums2* @param nums2_len*/public static void merge2(int[] nums1, int nums1_len, int[] nums2, int nums2_len) {int  n = nums1_len + nums2_len - 1;int  len_1 = nums1_len - 1, len_2 = nums2_len - 1;while (len_1 >= 0 && len_2 >= 0){if (nums1[len_1] >= nums2[len_2]){nums1[n--] = nums1[len_1--];}else if (nums1[len_1] < nums2[len_2]){nums1[n--] = nums2[len_2--];}}// 有剩余while(len_1 != -1){nums1[n--] = nums1[len_1--];}while(len_2 != -1){ // 为甚是-1nums1[n--] = nums2[len_2--];}}