前言
Verilog中的signed是一个很多人用不好,或者说不太愿意用的一个语法。因为不熟悉它的机制,所以经常会导致运算结果莫名奇妙地出错。其实了解了signed以后,很多时候用起来还是挺方便的。
signed的使用方法主要有两种,其中一种是定义一个有符号数变量,例如:
reg [3:0] us_a; //定义无符号数us_areg signed [3:0] s_a; //定义有符号数s_a
这样定义以后,即使是将同一个值 1111 分别赋值给us_a和s_a,它们所表达的数也不同了,无符号数us_a是 15 ,而有符号数 s_a则是 -1 。但是,这个-1和15是人类或者说工具站在如何解释符号位的角度上解读的,在电路底层,它们的值都是一样的1111。所以signed相当于只是规定了如何来解读一个数的最高有效位。
signed还有一个用法是强制转换,把一个无符号数转换为有符号数类型。例如:
reg [7:0] regA;regA = $signed(-4);
这两个是signed的一般语法,而它的本质在我看来只有两点:
- 当计算不产生溢出的时候,signed只影响如何将2进制数解读为10进制数;
- 当计算产生溢出的时候,signed影响的是如何对高位扩展–无符号数高位扩展0,而有符号数则高位扩展符号位。
计算结果不溢出
来看下面的代码:
`timescale 1ns/1ns
module tb_test();reg [3:0] us_a,us_b; //无符号加数a、加数b
reg signed [3:0] s_a,s_b; //有符号加数a、加数b
reg [3:0] us_sum; //无符号和
reg signed [3:0] s_sum; //有符号和initial beginus_a = 4'b1001; //9us_b = 4'b0001; //1s_a = 4'b1001; //-7s_b = 4'b0001; //3#10 us_sum = us_a + us_b; //9+1s_sum = us_a + us_b; //9+1
#10 us_sum = us_a + s_b; //9+1s_sum = us_a + s_b; //9+1
#10us_sum = s_a + us_b; //-7+1s_sum = s_a + us_b; //-7+1
#10 us_sum = s_a + s_b; //-7+1s_sum = s_a + s_b; //-7+1end endmodule
加数a和加数b分别定义成有符号数和无符号数,加数的和也分别定义成有符号数和无符号数,这样一共有2×2×2 =8 种组合。
给a赋值1001(即无符号数 9/有符号数 -7);给b赋值0001(即无符号数 1/有符号数 1),可以看到他们的计算结果都是一样的1010(即无符号数 10/有符号数 -6):
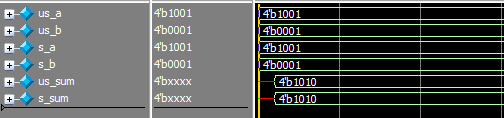
这个结果和预期是一致的。两个二进制数的加法,因为和没有溢出,所以不管是定义成有符号的还是无符号的,它们的结果肯定都一样。原因就是前面说的第一点:
当计算不产生溢出的时候,signed只影响如何将2进制数解读为10进制数;
计算结果溢出
现在将上面的代码改一下,把和改成5位,使他们的结果需要强制溢出(扩宽)到5位,如下:
reg [4:0] us_sum; //无符号和
reg signed [4:0] s_sum; //有符号和
仿真结果已经和上面不同了:
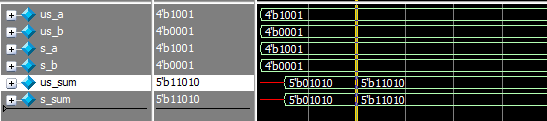
前面3种计算的结果仍然没变,但是第4种计算(即两个有符号数相加)的结果从0_1010变成了1_1010,也就是说最高位的符号位扩展了一位。有符号数和无符号数的运算有一个规则:
不管运算结果是有符号数还是无符号数,只要右边运算式中有一个是无符号数,那么运算结果就是无符号数。
也就是说
- 无符号数 + 无符号数 的结果是 无符号数
- 有符号数 + 无符号数 的结果是 无符号数
- 有符号数 + 有符号数 的结果是 有符号数
因为前3种运算中都有 无符号数 参与,所以不管 和 是定义成有符号数还是无符号数 ,它们的结果都是 无符号数,所以会在高位拓展0;而第4种运算则是只有 有符号数 参与,所以它们的结果都会在高位扩展符号位(即1)。
再来看一个例子:
`timescale 1ns/1ns
module tb_test();reg signed [1:0] s_a ;
reg [1:0] us_a;reg [3:0] s_s_a ;
reg [3:0] us_us_a;
reg [3:0] inv_s_a ;
reg [3:0] inv_us_a;initial begins_a = -1;us_a = -1;s_s_a = s_a;us_us_a = us_a;inv_s_a = - s_a;inv_us_a = - us_a;
end endmodule
仿真结果是这样的:
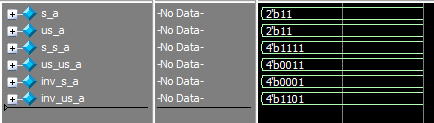
- s_a和us_a的赋值都是 -1,实际就是32‘b111···111,位宽只有2位,所以被截断到2’b11。
- s_s_a是s_a的高位扩展,因为s_a是有符号数,所以高位扩展补符号位1,就从11变成1111;us_us_a是us_a的高位扩展,因为us_a是无符号数,所以高位扩展补0,从从11变成0011。
- inv_s_a是s_a的数值的相反数,即补码按位取反后再加1,s_a先从11拓展到1111,再取反加1就变成了0001。从十进制的角度看 s_a(11)是 -1,而 inv_s_a是0001(1),符合相反数的关系。
- inv_us_a是us_a的数值的相反数,即补码按位取反后再加1,us_a先从11拓展到0011,再取反加1就变成了1101。从十进制的角度看 us_a(11)是 3,而 inv_s_a是1101(-3),也符合相反数的关系。
signed的用法
自动扩展位宽
将一个数的位宽扩展,如果不使用signed语法,则首先需要判断其最高位是否为1,如果是则说明是负数,高位需要扩展1;如果不是则说明是正数,那么高位需要扩展0(正数也可直接赋值,因为不使用signed的话工具会自动扩展0),例如:
module test
(input [3 : 0] in,output reg [4 : 0] out
);always@(*)
beginif(~in) //in是正数out = in; //直接赋值,等价于高位补0 out = {1'b0,in};else //in是负数out = {1'b1,in}; //高位保护1
endendmodule
如果使用signed就可以直接赋值了,例如:
module test
(input signed [3 : 0] in,output signed [4 : 0] out
);assign out = in; //直接赋值,等价于自动判断高位补符号位endmodule
简化运算
考虑两个4bits数的加法,为了防止结果溢出,把和的位宽设定成5bits。假如两个数分别为0101(5)和1100(-4),则二者的和应该为 (5 - 4 = 1),但实际结果为 0101 + 1100 = 10001(-15),二者显然对不上。
在不使用signed的情况下,我们需要做的是把两个加数分别扩展符号位,然后再相加。0101扩展到00101 ,1100扩展到11100,这样二者相加为 01001 + 11100 = 10_0001,因为结果只有5bits,所以会被截断到00001,也就是1,这样结果就能对上了。代码是这样写的:
module test
(input [3 : 0] in1,in2,output [4 : 0] out
);assign out = {in1[3],in1} + {in2[3],in2}; //手动补充高位的符号位endmodule
而如果将加数都定义成signed类型,则可以直接相加,综合工具会自动在高位扩展符号位来完成计算:
module test
(input signed [3 : 0] in1,in2,output signed [4 : 0] out
);assign out = in1 + in2; //手动补充高位的符号位endmodule
移位操作
不使用signed的情况下,右移首先需要根据最高位的符号来判断这个数是正数还是负数,正数右移需要高位补0,而负数右移则需要高位补1。
比如 -4 右移一位的结果应该是 -2,即4’b1100 >>1 的结果应该是4’b1110,如果高位补0则成了4‘b0110(6),结果就明显错了。所以代码要这么写:
module test
(input [3 : 0] in,output reg [3 : 0] out
);//右移两位
always@(*)
beginout = in >> 2; //首先右移两位,先默认在高位补0,后面再根据判断来修改if(in[3]) //in是负数out [3:2] = 2'b11; //高位补的0替换成1
endendmodule
如果将数据定义成了signed类型,则不需要判断正负,可以直接使用 算术右移预算符 >>> 来做移位。算术右移时,高位补充的是符号位。算术右移需要和signed一起使用,因为无符号数的算术右移补充的是0。代码:
module test
(input signed [3 : 0] in,output signed [3 : 0] out
);//右移两位
assign out = in >>> 2; //算术右移高位会自动补符号位endmodule
比较
在不定义signed的情况下,只要比较中出现了负数,那么比较的结果就不能直接对比了,直接对比很容易出错,比如:
`timescale 1ns/1ns
module tb_test();reg [3:0] a,b;initial begina = 4'd1; //1b = -4'd3; //-3if(a > b)$display("a > -3");else$display("a < -3");
end endmodule
这段打印的结果居然是:
a < -3
也就是说 1居然小于 -3 ?结果明显不对。如果不使用signed来定义变量,那么在判断两个数的大小时,首先需要判断符号位,然后才是判断剩余数的大小。这样写出来的代码非常麻烦。如果把两个数都定义成signed类型,那就可以直接对比了:
module test
(input signed [3:0] in1,in2,output out
);//当in1大于in2时输出1;其他时候输出0;不考虑二者相等的情况
assign out = (in1 > in2) ? 1'b1 : 1'b0;endmodule
测试结果符合预期: