(一)马氏过程和泊松过程、维纳过程的联系
泊松过程、维纳过程两者都是独立增量过程。独立增量过程是马氏过程的条件:
1. 随机过程是独立增量过程
2. X(0)= 0
满足以上两个条件的随机过程都是马氏过程。


注意:
上述结论的证明通过马氏过程的定义完成,即证明第j个和第n个独立增量相互独立,且该结论用到了第3章第4节的一个重要定理。
从该例题,我们可以得出结论,初始值为0的独立增量随机过程一定是马氏过程,而且x(0) = 0是必要条件,不可或缺。但是反过来,马氏过程不一定是初始值为0的独立增量随机过程。
题目虽然简单,但是理解起来还是有一些深度的。
马氏过程的定义:
P { X n ∣ x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } = P { X n , x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } P { x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } = P { X n ∣ x n − 1 } P\{ X_n | x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\} = \\ \frac{ P\{ X_n ,x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\}}{P\{ x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\} } = P\{ X_n | x_{n-1}\} P{Xn∣xn−1,xn−2,xn−3,...,x1,x0}=P{xn−1,xn−2,xn−3,...,x1,x0}P{Xn,xn−1,xn−2,xn−3,...,x1,x0}=P{Xn∣xn−1}
根据上式的定义,由随即变量的独立性可得:
P { X n ∣ x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } = P { X n ∣ x n − 1 } P { x n − 2 } P { x n − 3 } . . . P { x 1 } P { x 0 } P\{ X_n | x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\} = P\{ X_n | x_{n-1}\} P\{x_{n-2}\}P\{x_{n-3}\}...P\{x_{1}\}P\{x_{0}\}\\ P{Xn∣xn−1,xn−2,xn−3,...,x1,x0}=P{Xn∣xn−1}P{xn−2}P{xn−3}...P{x1}P{x0}
(二)均方积分存在条件的个人理解
关于均方积分的定义和性质:
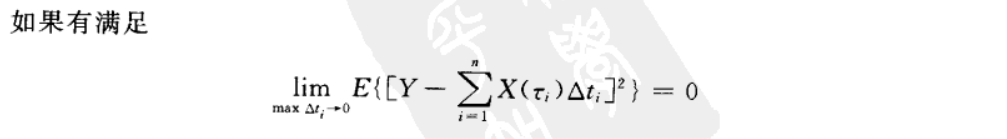

下面简单阐述一下自己对上图中两个结论的理解。
设 ∑ i = 1 n X ( τ i ) Δ t i = A \sum_{i=1}^{n}X(\tau _{i}) \Delta t_{i} = A ∑i=1nX(τi)Δti=A,则上图中的均方积分可以化为:
lim m a x Δ t i → 0 E { [ Y − ∑ i = 1 n X ( τ i ) Δ t i ] 2 } = E ( Y 2 − 2 A Y + A 2 ) = E ( Y 2 ) + E ( A 2 ) − 2 E ( A Y ) = 0 \lim _{max \Delta t_{i} \to 0}E \{ \biggl [ Y - \sum_{i=1}^{n}X(\tau _{i}) \Delta t_{i} \biggr ] ^{2}\} = \\ E(Y^2 - 2AY + A^2) = E(Y^2) + E(A^2) - 2E(AY) = 0 maxΔti→0limE{[Y−i=1∑nX(τi)Δti]2}=E(Y2−2AY+A2)=E(Y2)+E(A2)−2E(AY)=0
即:
E ( Y 2 ) + E ( A 2 ) = 2 E ( A Y ) E(Y^2) + E(A^2) = 2E(AY) E(Y2)+E(A2)=2E(AY)
从而得出一个满足上述等式的解:A = Y 即:
Y = ∑ i = 1 n X ( τ i ) Δ t i = ∫ a b X ( τ ) d τ Y = \sum_{i=1}^{n}X(\tau _{i}) \Delta t_{i} = \int _{a} ^{b} X(\tau) d \tau Y=i=1∑nX(τi)Δti=∫abX(τ)dτ
上图提到,均方积分存在的充分条件是存在:
∫ a b ∫ a b X ( s ) X ( t ) d s d t = ∫ a b X ( s ) d s ∫ a b X ( t ) d t \int _{a}^{b} \int _{a}^{b} X(s) X(t) ds dt = \int _{a}^{b} X(s) ds \int _{a}^{b} X(t) dt ∫ab∫abX(s)X(t)dsdt=∫abX(s)ds∫abX(t)dt
根据积分的定义,上式的含义是两个原函数在区间[a, b]上的差值的乘积,该差值正好是: ∑ i = 1 n X ( τ i ) Δ x 或者 ∫ a b X ( τ ) d τ \sum _{i=1} ^{n} X( \tau _{i}) \Delta x 或者 \int _{a} ^{b} X(\tau) d \tau i=1∑nX(τi)Δx或者∫abX(τ)dτ
因此可以简略的证明,上图中的结论是充分的。
![[数据分析与可视化] Python绘制数据地图5-MovingPandas绘图实例](https://img-blog.csdnimg.cn/img_convert/27d0e108fa1ee2c9ea997ab4c1812057.png)