Softmax 函数和 Gibbs 分布之间的数学桥梁

一、说明

   softmax 函数是各种神经网络中的基本元素，尤其是那些为分类任务而设计的神经网络。它有效地将实值分数 （logits） 的向量从神经网络的最终线性输出转换为概率分布。softmax 输出的每个组件都表示输入属于特定类的概率。

二、Softmax 函数的定义和组件

   通过在机器学习中的softmax函数和物理学中的吉布斯分布之间建立相似之处，我们可以更好地理解控制这两个领域的基本原理。这些见解不仅增强了我们对神经网络行为的理解，而且还证明了指数族分布在不同科学学科中的普遍性。

   softmax 函数（表示为 σσ）应用于包含来自网络的原始分数的向量 z，并为每个分量 zi 定义如下：

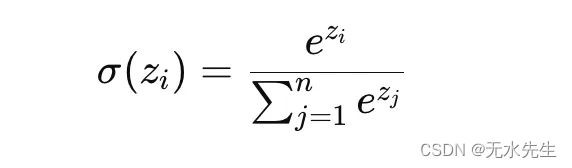
其中 i 的范围为 1 到 n，是类的总数。

详细的成分分析
   $z_i$：这些是每个类的逻辑数，或神经网络最后一层的原始输出分数。
   $e^{z_i}$：将指数函数应用于每个 logit，将每个分数转换为正数。
   $j=\mathrm{1..}n{e}^{z_j}$：这个归一化因子，即所有指数分数的总和，确保 softmax 输出的总和为 1，形成有效的概率分布。

三、从逻辑到多类的泛化

   Softmax 是逻辑函数的扩展，用于二元分类。虽然逻辑函数输出两个类的概率，但 softmax 扩展了这个框架以容纳多个类。

3.1 连接到 Gibbs 分布

   在统计力学中，softmax 公式类似于吉布斯分布，其中 e^zi 对应于能态 zi 的玻尔兹曼因子，分母的作用类似于分配函数，使分布归一化。

   softmax 函数和 Gibbs 分布之间的联系是机器学习和统计力学之间的一个引人入胜的交叉点。这种联系提供了对神经网络如何对概率建模以及物理学概念如何阐明复杂机器学习算法行为的深刻见解。让我们更深入地研究数学框架来理解这种关系。

3.2 统计力学背景

   在统计力学中，吉布斯分布（也称为玻尔兹曼分布）描述了系统在热平衡的一组可能状态中处于某种状态 i 的概率 Pi。系统处于状态 i 的概率由下式给出：

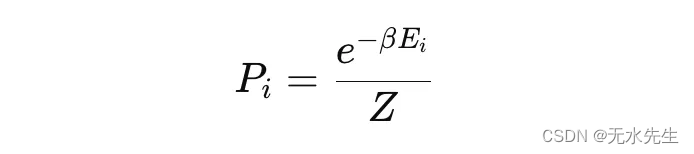
这里：

   Ei 是状态 i 的能量。
   β是反温度因子（通常定义为 β=1/（k_B。T），其中 k_B 是玻尔兹曼常数，T 是温度）。
   Z 是分区函数，它是一个归一化因子，确保概率之和为 1。它被定义为：

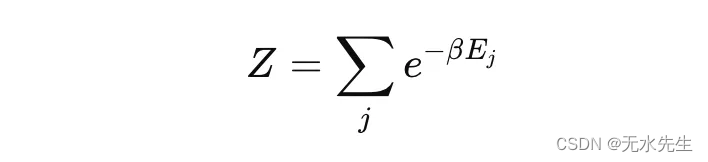
3.3 切换到 Softmax 功能

   为了查看与吉布斯分布的平行关系，将 softmax 函数中的 logits zi 视为类似于统计力学中的负能量状态 −Ei，并将逆温度β解释为设置为 1 以简单起见。然后，softmax 方程转换为类似于 Gibbs 分布的形式：

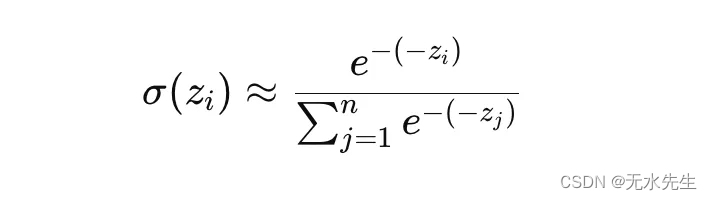
   在此配方中：

   zi 扮演的角色类似于 Ei，这意味着更高的 logits（更少的负“能量”）会导致更高的概率，反映了物理学中低能量状态的可能性更大。
softmax 函数分母中的总和类似于分区函数 Z，将输出归一化为概率分布。
熵和自由能

   在统计力学中，吉布斯分布是通过最小化亥姆霍兹自由能 F=E−TS 得出的，其中 E 是预期能量，T 是温度，S 是熵。这种最小化自由能的原理可以类比地应用于机器学习，在机器学习中，人们可能会认为最小化损失函数可以减少预测模型的一种“信息自由能”形式。

四、优化和计算稳定性

   指数变换确保以稳定的方式放大对数之间的差异。这对于保持非零梯度和确保有效的基于梯度的学习至关重要。

4.1 Softmax 的梯度

   了解 softmax 的梯度对于反向传播至关重要：

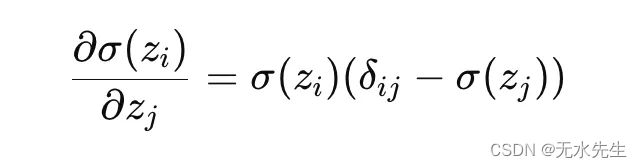
   其中 δij 是克罗内克三角洲。这显示了一个类的概率对 logit 变化的依赖性，这对于更新神经网络的权重至关重要。

4.2 链接到信息论

   将softmax与交叉熵损失相结合与信息论中的概念有关。交叉熵测量预测概率与实际分布之间的信息距离，指导模型最小化这种差异。

   从 Log-Sum-Exp 派生 Softmax
   Softmax 可以从 log-sum-exp 函数导出，这是一个平滑的最大函数近似：

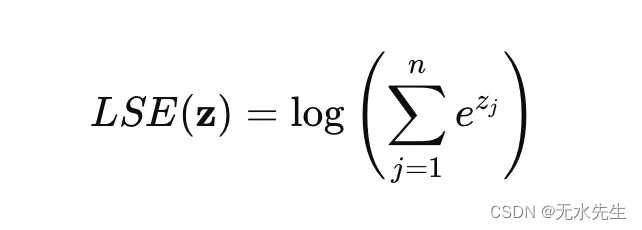
将 LSE（z）LSE（z） 相对于 zizi 进行微分，可得到 softmax 函数：

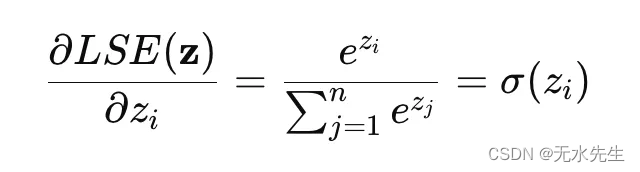
   这个推导说明了softmax是如何从最大化似然函数和操纵对数尺度中的概率来实现数值稳定性的。

五、总结

   softmax函数是神经网络分类架构的基石，为输出归一化和概率计算提供了强大的机制。它的数学基础不仅促进了实用的学习算法，而且丰富了其理论理解。

   我邀请大家分享他们的见解或提出有关softmax的详细数学或其在各个领域的应用的问题。您的观点丰富了讨论，并加深了我们对高级神经网络技术的集体理解。