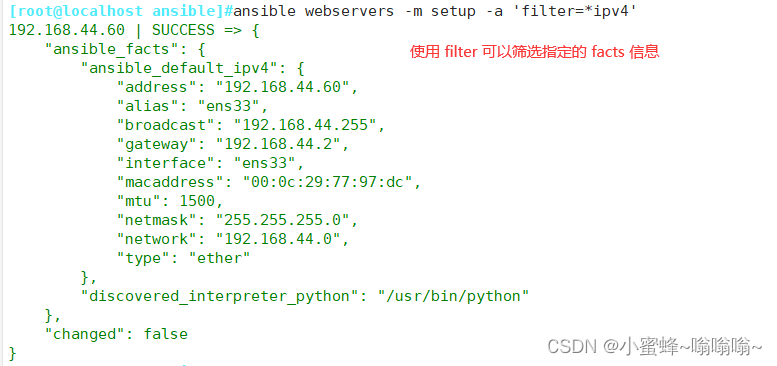
目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2023年,Y Gao受到PID控制理论启发,提出了PID搜索算法(PID-based Search Algorithm, PSA)。


2.算法原理
2.1算法思想
PID算法是控制领域的经典算法,分为增量PID控制和位置PID控制,它通过偏差的比例(P)、积分(I)和微分(D)进行控制。PSA通过连续调整系统偏差将整个种群收敛到最优状态。
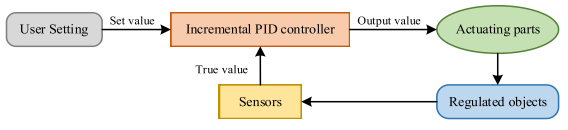
2.2算法过程
增量PID控制
计算系统偏差对于最小化问题,迭代次数t处的最佳个体x*(t)是对应于总体历史最小值的个体。多次迭代t的总体偏差ek(t):
e k ( t ) = x ∗ ( t − 1 ) − x ( t − 1 ) (1) \mathbf e_k(t)=\mathbf x^*(t-1)-\mathbf x(t-1)\tag{1} ek(t)=x∗(t−1)−x(t−1)(1)
为了便于计算和迭代更新:
e k − 1 ( t ) = e k ( t − 1 ) + x ∗ ( t ) − x ∗ ( t − 1 ) (2) \mathbf{e}_{k-1}(t)=\mathbf{e}_k(t-1)+x^*(t)-x^*(t-1)\tag{2} ek−1(t)=ek(t−1)+x∗(t)−x∗(t−1)(2)
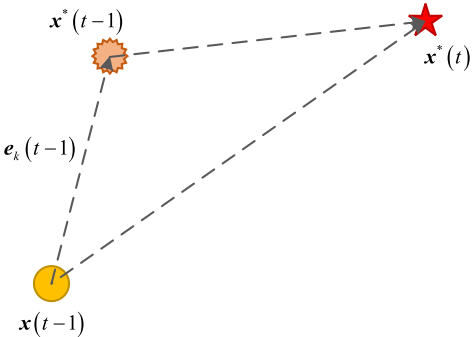
PID调节
在现实问题中,比例、积分和微分因子会根据不同的情况和问题进行调整。当迭代次数为t时,PID调节的输出值Δu(t):
Δ u ( t ) = K p ⋅ r 2 ⋅ [ e k ( t ) − e k − 1 ( t ) ] + K i ⋅ r 3 ⋅ e k ( t ) + K d ⋅ r 4 ⋅ [ e k ( t ) − 2 e k − 1 ( t ) + e k − 2 ( t ) ] (3) \begin{aligned}\Delta\mathbf{u}(t)=K_{p}\cdot\mathbf{r}_{2}\cdot[\mathbf{e}_{k}(t)-\mathbf{e}_{k-1}(t) ]+K_{i}\cdot\mathbf{r}_{3}\cdot\mathbf{e}_{k}(t)+K_{d}\cdot\mathbf{r}_{4}\cdot[\mathbf{e}_{k}(t)-2\mathbf{e}_{k-1}(t)+\mathbf{e}_{k-2}(t) ]\end{aligned}\tag{3} Δu(t)=Kp⋅r2⋅[ek(t)−ek−1(t)]+Ki⋅r3⋅ek(t)+Kd⋅r4⋅[ek(t)−2ek−1(t)+ek−2(t)](3)
其中r2、r3和r4是n行1列中从0到1的随机数的矢量;Kp、Ki和Kd分别是比例、积分和微分的调整系数,论文中分别设置为1、0.5和1.2。
在传统的PID算法中,输出调节值为0意味着实际值在某个点上已经达到设定值。但是,随着时间的增加,如果不调整受控对象,则真实值很快将不等于设定值。因此,增加了一个称为零输出的条件因子,以防止算法陷入局部最优:
o ( t ) = ( cos ( 1 − t / T ) + λ r 5 ⋅ L ) ⋅ e k ( t ) (4) \mathbf{o}(t)=(\cos(1-t/T)+\lambda\mathbf{r}_5\cdot\mathbf{L})\cdot\mathbf{e}_k(t)\tag{4} o(t)=(cos(1−t/T)+λr5⋅L)⋅ek(t)(4)
其中,r5是n行和d列中从0到1的随机数的矢量,λ是调整系数:
λ = [ ln ( T − t + 2 ) / ln ( T ) ] 2 (5) \lambda=\left[\ln(T-t+2)/\ln(T)\right]^2\tag{5} λ=[ln(T−t+2)/ln(T)]2(5)
λ随着t的增加而缓慢减小,这有前期算法充分探索。在后期,λ迅速下降,这有助于算法从探索转向开发。个体的更新都与Δu(t)和o(t)有关:
x ( t + 1 ) = x ( t ) + η ⋅ Δ u ( t ) + ( 1 − η ) ⋅ o ( t ) (6) \mathbf{x}(t+1)=\mathbf{x}(t)+\eta\cdot\Delta\mathbf{u}(t)+(1-\eta)\cdot\mathbf{o}(t)\tag{6} x(t+1)=x(t)+η⋅Δu(t)+(1−η)⋅o(t)(6)
其中,η是n行1列的矩阵:
η = r 6 cos ( t / T ) (7) \eta=\mathbf{r}_6\cos(t/T)\tag{7} η=r6cos(t/T)(7)
流程图

伪代码


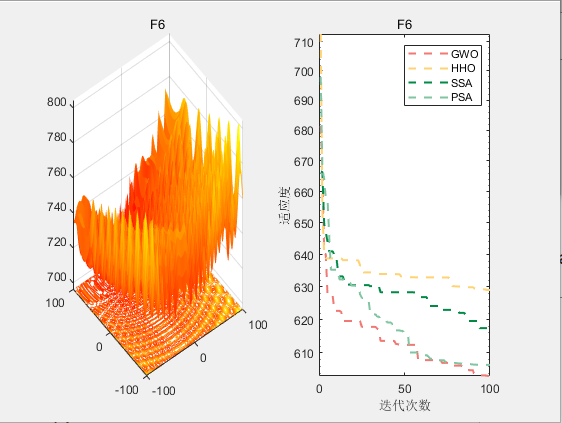
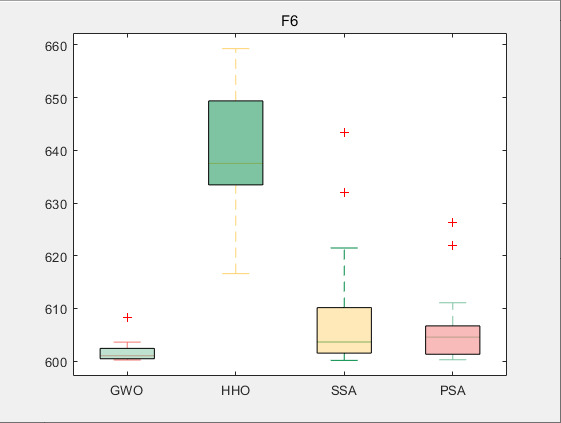
3.结果展示
使用测试框架,测试PSA性能 一键run.m
- 【智能算法】省时方便,智能算法统计指标——一键运行~
CEC2017-F6

4.参考文献
[1] Gao Y. PID-based search algorithm: A novel metaheuristic algorithm based on PID algorithm[J]. Expert Systems With Applications, 2023, 232: 120886.
![[Flutter]创建一个私有包并使用](https://img-blog.csdnimg.cn/direct/8396ab73e6084503a899618ead7d0154.png)




