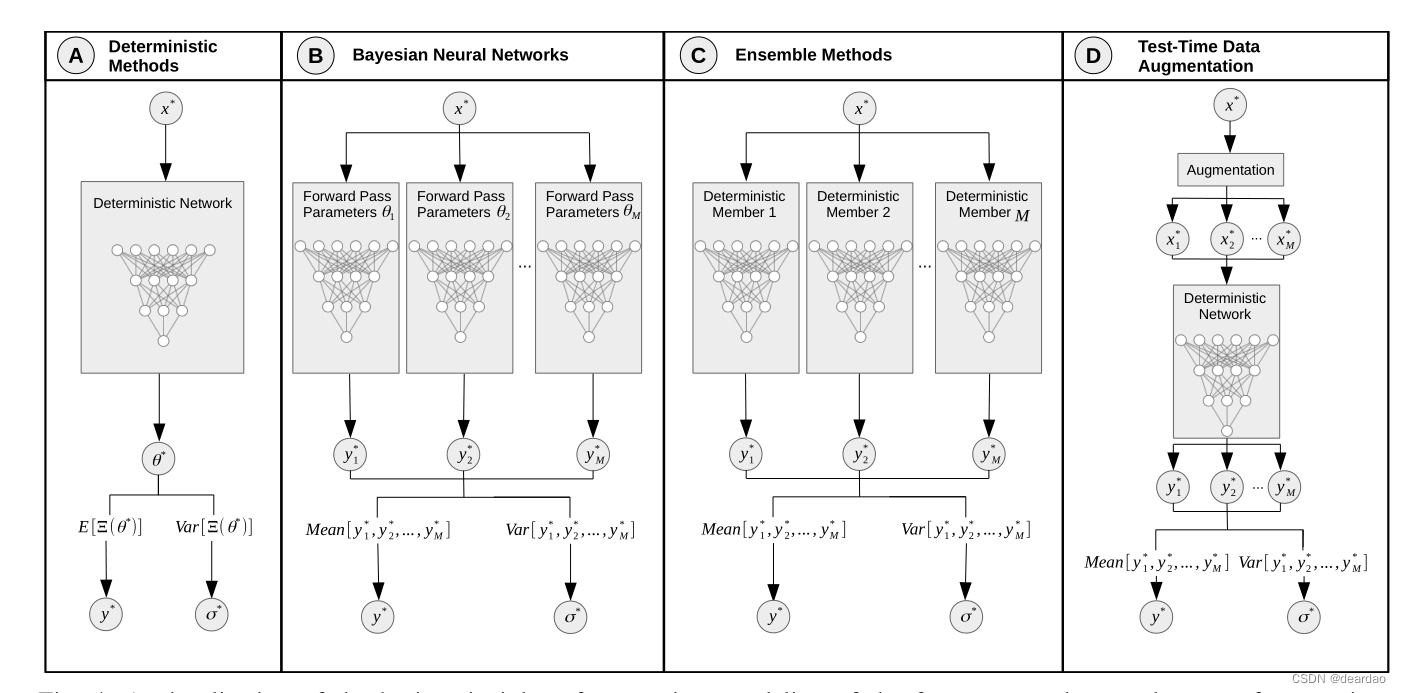
A.单一确定性方法
对于确定性神经网络,参数是确定的,每次向前传递的重复都会产生相同的结果。对于不确定性量化的单一确定性网络方法,我们总结了在确定性网络中基于单一正向传递计算预测y *的不确定性的所有方法。在文献中,可以找到几种这样的方法。它们大致可以分为两种方法,一种是对单个网络进行显式建模和训练,以量化不确定性[44]、[32]、[92]、[64]、[93];另一种是使用附加组件对网络的预测进行不确定性估计[46]、[36]、[71]、[72]。对于第一种类型,不确定性量化影响网络的训练过程和预测,而后一种类型通常应用于已经训练好的网络。由于经过训练的网络没有被这些方法修改,它们对网络的预测没有影响。下面,我们将这两种类型称为内部和外部不确定性量化方法。
1)内部不确定性量化方法:许多内部不确定性量化方法遵循预测分布参数的思想,而不是直接的逐点最大后验估计。通常,此类网络的损失函数会考虑真实分布与预测分布之间的期望散度,例如[32]、[94]。输出上的分布可以解释为模型不确定性的量化(参见第二节),试图模拟网络贝叶斯建模的行为。
对于分类任务,输出通常表示类概率。这些概率是应用softmax函数的结果。这些概率已经可以解释为对数据不确定性的预测。然而,人们普遍认为神经网络往往过于自信,而softmax输出往往校准不当,导致不确定度估计不准确[95]、[67]、[44]、[92]。此外,softmax的输出不能与模型的不确定性相关联。但是,如果没有明确地考虑到模型的不确定性,分布外样本可能导致证明错误置信度的输出。例如,对猫和狗进行训练的网络,当给它喂食鸟的图像时,很可能不会产生50%的狗和50%的猫。这是因为网络从图像中提取特征,即使这些特征不适合猫类,它们可能更不适合狗类。因此,网络将更多的概率放在cat上。此外,研究表明,整流线性单元(ReLu)网络和softmax输出的组合导致网络随着分布外样本之间的距离变得越来越自信。

图5显示了一个示例,其中从MNIST中旋转一个数字会导致具有高softmax值的错误预测。Hein等人对这一现象进行了描述和进一步研究[96],他们提出了一种避免这种行为的方法,该方法基于强制远离训练数据的均匀预测分布。其他几种分类方法[44],[32],[94],
[64]采用了类似的思想,考虑了logit幅度,但使用了Dirichlet分布。狄利克雷分布是分类分布的共轭先验,因此可以解释为分类分布上的分布。
不确定度度量和质量
下面,我们提出了量化不同预测类型的不确定性的不同措施。一般来说,这些不确定性的正确性和可信度并不是自动给出的。事实上,有几个原因可以解释为什么评估不确定性评估的质量是一项具有挑战性的任务。
- 首先,不确定性估计的质量取决于估计不确定性的基本方法。Yao等人的研究[256]证明了这一点,该研究表明贝叶斯推理的不同近似(例如高斯近似和拉普拉斯近似)会导致不同质量的不确定性估计。
- 其次,缺乏真值不确定性估计[31],并且定义真值不确定性估计具有挑战性。例如,如果我们将基础真理不确定性定义为人类受试者的不确定性,我们仍然需要回答“我们需要多少受试者?”或“如何选择科目?”
- 第三,缺乏统一的定量评价指标[257]。更具体地说,不确定性在不同的机器学习任务中有不同的定义,如分类、分割和回归。例如,预测间隔或标准差用于表示回归任务中的不确定性,而熵(和其他相关度量)用于捕获分类和分割任务中的不确定性。
A 评估分类任务中的不确定性
对于分类任务,网络的softmax输出已经就绪,代表了一种信心的度量。但由于原始的softmax输出既不太可靠[67],也不能代表所有的不确定性来源[19],因此开发了进一步的方法和相应的措施。
1 测量分类任务中的数据不确定性
考虑一个分类任务,有K个不同的类,对于一些输入样本x,有一个概率向量网络输出p(x),下面p用于简化,pk表示向量中的第K个条目。一般来说,给定的预测p代表一个分类分布,即它为每个类别分配一个正确预测的概率。由于预测不是作为显式类给出的,而是作为概率分布给出的,因此(不)确定性估计可以直接从预测中导出。一般来说,这种逐点预测可以看作是估计的数据不确定性[60]。然而,如第二节所述,模型对数据不确定性的估计受到模型不确定性的影响,必须单独考虑。为了评估预测数据不确定性的数量,例如可以应用最大类概率或熵度量:
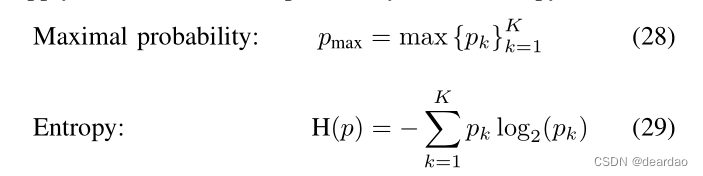
最大概率代表了确定性的直接表示,而熵描述了随机变量中信息的平均水平。即使softmax输出应该代表数据的不确定性,人们也不能从单个预测中判断出影响该特定预测的模型不确定性的量有多大。
2 分类任务中模型不确定性的测量
正如第三节已经讨论的那样,单一的softmax预测并不是一种非常可靠的不确定性量化方法,因为它通常校准得很差[19],并且没有关于模型本身对该特定输出的确定性的任何信息[19]。学习到的模型参数的(近似的)后验分布p(θ|D)有助于得到更好的不确定性估计。有了这样的后验分布,softmax输出本身就变成了一个随机变量,人们可以评估它的变化,即不确定性。为简单起见,我们将p(y|θ, x)也表示为p,从上下文中可以清楚地看出p是否依赖于θ。最常见的测量方法是互信息(MI)、预期Kullback-Leibler散度(EKL)和预测方差。基本上,所有这些度量都计算(随机)softmax输出和期望softmax输出之间的期望散度:
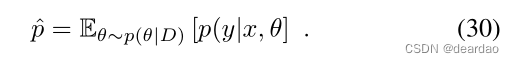
MI使用熵来度量两个变量之间的相互依赖性。在所描述的情况下,将期望softmax输出中给出的信息与softmax输出中期望信息之间的差进行比较,即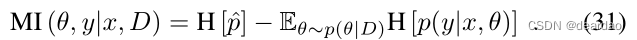
Smith和Gal[19]指出,当关于模型参数的知识不增加最终预测中的信息时,MI是最小的。因此,MI可以被解释为模型不确定性的度量。
Kullback-Leibler散度度量两个给定概率分布之间的散度。EKL可用于测量可能的softmax输出之间的(预期)散度,
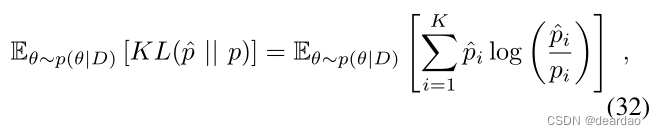
它也可以被解释为对模型输出的不确定性的度量,因此代表了模型的不确定性。
预测方差评估(随机)softmax输出上的方差,即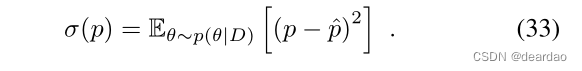
如第三节所述,分析描述的后置分布p(θ|D)仅适用于贝叶斯方法的一个子集。即使对于解析描述的分布,在几乎所有情况下,参数不确定性在预测中的传播也是难以处理的,必须进行近似,例如用蒙特卡罗近似。类似地,集成方法从M个神经网络收集预测,测试时间数据增强方法从应用于原始输入样本的M个不同的增强中接收M个预测。对于所有这些情况,我们收到一组M个样本,可用来近似难以处理甚至未定义的底层分布。有了这些近似值,(31)、(32)和(33)所规定的方法就可以直接应用,只需用平均值代替期望。例如,期望的softmax输出变成
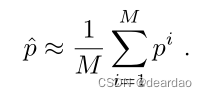
对于式(31)、式(32)和式(33)中给出的期望,期望近似相似。
3 分类中分布不确定性的测量任务
尽管这些不确定性度量被广泛用于捕获来自贝叶斯神经网络[60]、集成方法[31]或测试时间数据增强方法[14]的几种预测之间的可变性,但它们不能捕获输入数据或分布外示例中的分布变化,这可能导致有偏差的推断过程和错误的置信度陈述。如果所有的预测者都将高概率质量归因于相同的(错误的)类别标签,这将导致估计之间的低可变性。因此,网络似乎对其预测是确定的,而预测本身的不确定性(由softmax概率给出)也被评估为低。为了解决这个问题,第三节中描述的几种方法考虑了logit的大小,因为较大的logit表明相应类别的证据较多[44]。因此,这些方法要么将对数(指数)的总和解释为狄利克雷分布的精度值(参见第III-A节对狄利克雷先验的描述)[32]、[94]、[64],要么将其解释为与定义常数相比较的证据集合[44]、[92]。我们还可以分别为每个类推导出总类概率对每个logit应用sigmoid函数。基于类总概率,OOD样本可能更容易被检测到,因为所有类同时具有低概率。其他方法提供了一个显式的度量,新数据样本适合训练数据分布的程度。在此基础上,他们还给出了一个样本将被正确预测的度量[36]。
4 完全数据集上的性能度量
虽然上面描述的措施衡量单个预测的性能,但其他措施评估这些措施在一组样本上的使用情况。不确定度可以用来区分正确和错误分类的样本,或者区分域内和分布外的样本[67]。为此,将样本分成两组,例如域内和分布外,或正确分类和错误分类。最常用的两种方法是受试者工作特征(ROC)曲线和精确召回率(PR)曲线。这两种方法都基于底层度量的不同阈值生成曲线。对于每个考虑的阈值,ROC曲线绘制了真阳性率和假阳性率的对比图,PR曲线绘制了召回率和精度的对比图。虽然ROC和PR曲线提供了一个直观的概念,说明底层度量如何很好地适合于分离两个被考虑的测试用例,但它们并没有给出一个定性的度量。为了达到这个目的,可以评估曲线下面积(AUC)。粗略地说,AUC给出了一个随机选择的正样本比随机选择的负样本导致更高测量值的概率值。例如,最大softmax值衡量正确分类的示例比错误分类的示例的等级高。Hendrycks和Gimpel[67]表明,在几个应用领域中,正确的预测通常比错误的预测具有更高的softmax值的预测确定性。特别是对于域内和分布外示例的评估,常用的方法是Receiver Operating Curve (AUROC)和Precision Recall Curce (AUPRC)[64],[32],[94]。这些评估的明显缺点是,性能是评估的,最佳阈值是基于给定的测试数据集计算的。偏离测试集分布的分布可能会破坏整个性能,并使派生的阈值不切实际。