---

求组合数Ⅰ（递推）

适合场景：$1\le b\le a\le 2000$，取模情况下。

核心理论

$$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$$

通过递推的方式来求解。

理论推导

先把 $a$ 个元素分成两个部分：

• 第 $a$ 个元素
• 剩下的 $a-1$ 个元素

在选择 $b$ 个元素时，有两种情况：

• 选取第 $a$ 个元素
• 不选取第 $a$ 个元素

如果选取第 $a$ 个元素,那么我们需要从剩下的 $a-1$ 个元素中选择 $b-1$ 个元素。由组合数定义，这种情况的个数为 $C_{a-1}^{b-1}$。

如果不选取第 $a$ 个元素,那么我们需要从剩下的 $a-1$ 个元素中选择 $b$个元素。这种情况的个数为 $C_{a-1}^b$。

于是总的组合个数就等于上面两种情况之和：

$C_a^b=C_{a-1}^{b-1}+C_{a-1}^b$

典型例题

题目描述：
给定 $n$ 组询问，每组询问给定两个整数 $a,b$，请你输出 $C_a^b(\mathrm{m}\mathrm{o}\mathrm{d}10^9+7)$的值。

输入格式：
第一行包含整数 $n$。

接下来 $n$ 行，每行包含一组 $a$ 和 $b$。

输出格式：
共 $n$ 行，每行输出一个询问的解。

数据范围：
$1\le n\le 10000$
$1\le b\le a\le 2000$

输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;const int N = 2010, mod = 1e9 + 7;
int c[N][N];void Init()
{for (int i = 0; i < N; i++){for (int j = 0; j <= i; ++j)if (!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;}
}
int main()
{Init();int n;cin >> n;while (n--){int a, b;cin >> a >> b;cout << c[a][b] << endl;}return 0;
}

求组合数Ⅱ（预处理）

核心理论

适合场景：$1\le b\le a\le 10^5$，取模情况下。

$$C_a^b=\frac{a!}{(a-b)!\ast b!}$$

由于数据较大且可取模，因此通过求乘法逆元的方法来将 $\frac{a!}{(a-b)!\ast b!}$ 转换为 $a!\ast b!\ast {(a-b)!}^{-1}$ 的形式。

因此采用两个数组来递推：

$fact[i]=i!\%mod$
$infact[i]=(i!{)}^{-1}\%mod$

$$C_a^b=\frac{a!}{(a-b)!\ast b!}=(fact[a]\ast infact[a-b]\ast infact[b])$$

典型例题

题目描述：
给定 $n$ 组询问，每组询问给定两个整数 $a,b$，请你输出 $C_a^b(\mathrm{m}\mathrm{o}\mathrm{d}10^9+7)$的值。

输入格式：
第一行包含整数 $n$。

接下来 $n$ 行，每行包含一组 $a$ 和 $b$。

输出格式：
共 $n$ 行，每行输出一个询问的解。

数据范围：
$1\le n\le 10000$
$1\le b\le a\le 10^5$

输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;const int N = 1e5 + 10, mod = 1e9 + 7;
int fact[N]; // 阶乘结果数组
int infact[N]; // 阶乘逆元结果数组// 快速幂
int qmi(int a, int b, int p)
{int res = 1;while (b){if (b & 1) res = (long long)res * a % p;a = (long long)a * a % p;b >>= 1;}return res;
}
int main()
{fact[0] = infact[0] = 1;for (int i = 1; i < N; ++i) // 递推求解{fact[i] = (long long)fact[i - 1] * i % mod;infact[i] = (long long)infact[i - 1] * qmi(i, mod - 2, mod) % mod;}int n;cin >> n;while (n--){int a, b;cin >> a >> b;cout << (long long)fact[a] * infact[b] % mod * infact[a - b] % mod << endl;}return 0;
}

求组合数Ⅲ（Lucas定理）

适合场景：$1\le b\le a\le 10^{18}$，取模且模数为在 $1\le p\le 10^5$ 较小范围内的质数。

核心理论

Lucas（卢卡斯）定理：

1.Lucas定理的第一形式
KaTeX parse error: No such environment: align* at position 14: \LARGE \begin{̲a̲l̲i̲g̲n̲*̲}̲ C_a^b \equiv \…
其中：

• $a={\sum }_{i=0}^k{a}_i{p}^i$ 和 $b={\sum }_{i=0}^k{b}_i{p}^i$ 是 $a$ 和 $b$ 在素数 $p$ 的 $p$ 进制展开。

2.Lucas定理的第二形式
$$C_a^b\equiv C_{a\%p}^{b\%p}\ast C_{a÷p}^{b÷p}(\mathrm{m}\mathrm{o}\mathrm{d}p)$$

Lucas定理的证明

1.证明Lucas定理的第一形式

2.证明Lucas定理的第二形式

典型例题

题目描述：
给定 $n$ 组询问，每组询问给定三个整数 $a,b,p$，其中 $p$ 是质数，请你输出 $C_a^b(\mathrm{m}\mathrm{o}\mathrm{d}p)$ 的值。

输入格式：
第一行包含整数 $n$。

接下来 $n$ 行，每行包含一组 $a,b,p$。

输出格式：
共 $n$ 行，每行输出一个询问的解。

数据范围：
$1\le n\le 20$
$1\le b\le a\le 10^{18}$
$1\le p\le 10^5$

输入样例：

3
5 3 7
3 1 5
6 4 13

输出样例：

3
3
2

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;// 快速幂求逆元
int qmi(int a, int b, int p) 
{int res = 1;while (b){if (b & 1) res = (long long)res * a % p;a = (long long)a * a % p;b >>= 1;}return res; // 返回结果
}// 计算组合数 C(a, b) mod p
int C(int a, int b, int p)
{if (a < b) return 0; // 组合数要求 a >= bint facts = 1, infacts = 1;for (int i = 1; i <= b; ++i){facts = (long long)facts * (a - i + 1) % p; // 分子阶乘infacts = (long long)infacts * i % p; // 分母阶乘}return (long long)facts * qmi(infacts, p - 2, p) % p; // 分子阶乘 * 分母阶乘的逆元 mod p
}// Lucas 定理递归版  
int lucas(long long a, long long b, int p)
{if (a < p && b < p) // 递归终止条件return C(a, b, p); return (long long)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;// 按照 Lucas 定理递归计算
}int main()
{int n;cin >> n;while (n--){long long a, b;int p;cin >> a >> b >> p;cout << lucas(a, b, p) << endl;}return 0;
}

求组合数Ⅳ（高精度乘法及质因子优化）

适合场景：$1\le b\le a\le 5000$，且不取模的情况下。

核心理论

$$C_a^b=\frac{a!}{(a-b)!\ast b!}$$

由于不能取模，直接求阶乘会导致数据溢出。因此采用高精度乘法进行计算，但直接采用高精度乘法效率过低，因此采用分解质因子，将每个阶乘中的质因子出现个数计算出来，再利用高精度乘法来计算从而达到效率目的。

分解质因子：
$$C_a^b=p_1^{{\alpha }_1}\times p_2^{{\alpha }_2}\times p_3^{{\alpha }_3}...\times p_k^{{\alpha }_k}$$

计算阶乘中某质因子出现的个数：

$$cn{t}_{a!}=\lfloor \frac{a}{p}\rfloor +\lfloor \frac{a}{p^2}\rfloor +\lfloor \frac{a}{p^3}\rfloor +...+\lfloor \frac{a}{p^k}\rfloor$$

$$cn{t}_{b!}=\lfloor \frac{b}{p}\rfloor +\lfloor \frac{b}{p^2}\rfloor +\lfloor \frac{b}{p^3}\rfloor +...+\lfloor \frac{b}{p^k}\rfloor$$

$$cn{t}_{(a-b)!}=\lfloor \frac{a-b}{p}\rfloor +\lfloor \frac{a-b}{p^2}\rfloor +\lfloor \frac{a-b}{p^3}\rfloor +...+\lfloor \frac{a-b}{p^k}\rfloor$$

最后再利用高精度乘法对这些质因子进行乘法。

典型例题

题目描述：
输入 $a,b$，求 $C_a^b$ 的值。

注意结果可能很大，需要使用高精度计算。

输入格式：
共一行，包含两个整数 $a$ 和 $b$。

输出格式：
共一行，输出 $C_a^b$ 的值。

数据范围：
$1\le b\le a\le 5000$

输入样例：

5 3

输出样例：

10

代码实现

#include <iostream>
#include <vector>
using namespace std;const int N = 5010;
int primes[N], cnt;  // 存储素数的数组和素数的数量
int sum[N];  // 存储每个素数的质因子在组合数C(a, b)中的出现个数
bool st[N];  // 素数筛选标记数组// 获取小于等于x的所有素数
void get_primes(int x)
{for (int i = 2; i <= x; ++i){if (!st[i]) primes[cnt++] = i;  // 如果i是素数，添加到primes数组for (int j = 0; primes[j] <= x / i; ++j){st[primes[j] * i] = true;  // 筛选掉 i * primes[j]，标记为合数if (i % primes[j] == 0) break;  // 保证只被最小质因子筛}}
}// 计算一个阶乘数中素数p的幂次
int get(int x, int p)
{int res = 0;while (x){x /= p;res += x;}return res;
}// 高精度乘法
vector<int> mul(vector<int> a, int b)
{vector<int> res;for (int i = 0, t = 0; i < a.size() || t; ++i){if (i < a.size()) t += a[i] * b;res.push_back(t % 10);t /= 10;}return res;
}int main()
{int a, b;cin >> a >> b;get_primes(a);  // 获取小于等于a的所有素数vector<int> res;res.push_back(1);for (int i = 0; i < cnt; ++i){int p = primes[i];// 计算每个素数的质因子在C(a, b)中的出现个数sum[i] = get(a, p) - get(b, p) - get(a - b, p);// 根据每个素数的质因子出现个数更新结果for (int j = 0; j < sum[i]; ++j) res = mul(res, p);}// 输出计算结果for (int i = res.size() - 1; i >= 0; --i) cout << res[i];cout << endl;return 0;
}

求组合数Ⅴ（卡特兰数）

卡特兰数的概念

卡特兰数（$Catalannumber$）是 组合数学 中一个常出现在各种 计数问题 中的 数列。

前几个卡特兰数依次为：$1,1,2,5,14,42,132,429,1430,4862，...$

对于任意的自然数 $n$，第 $n$ 个卡特兰数按下列公式定义:

$$C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}$$

卡特兰数的应用场景

1.进出栈序列

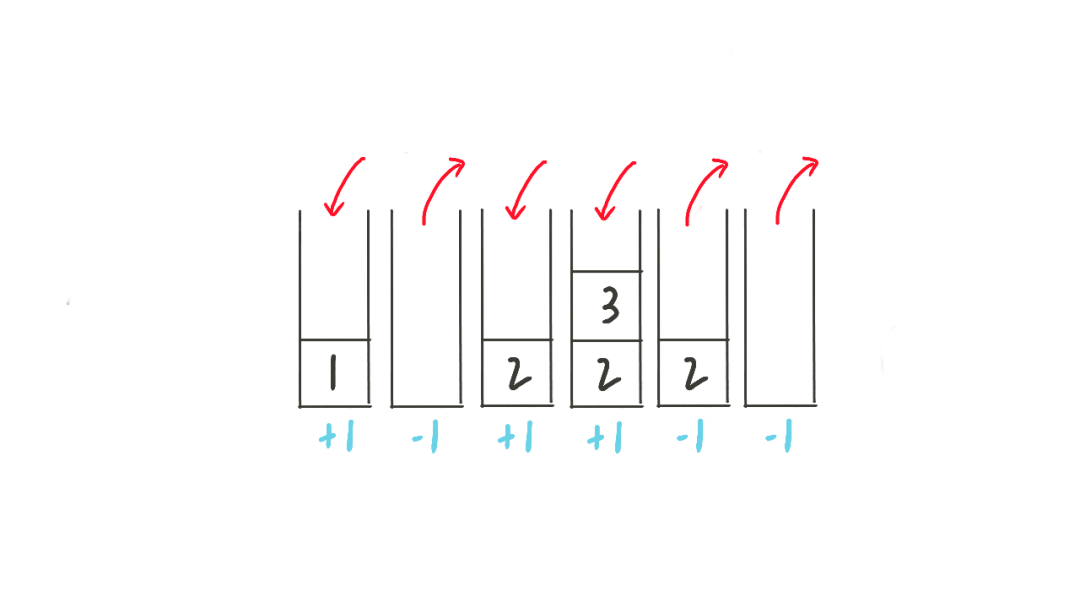
2.括号序列

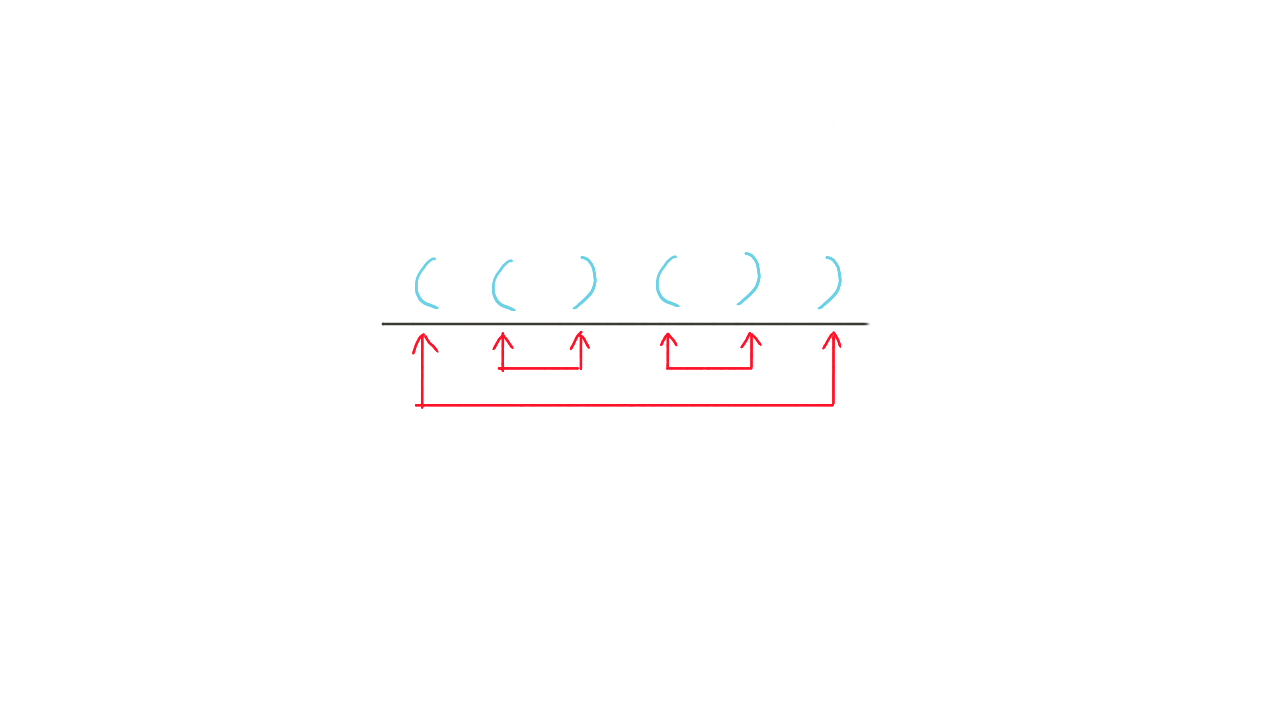
3.二叉树

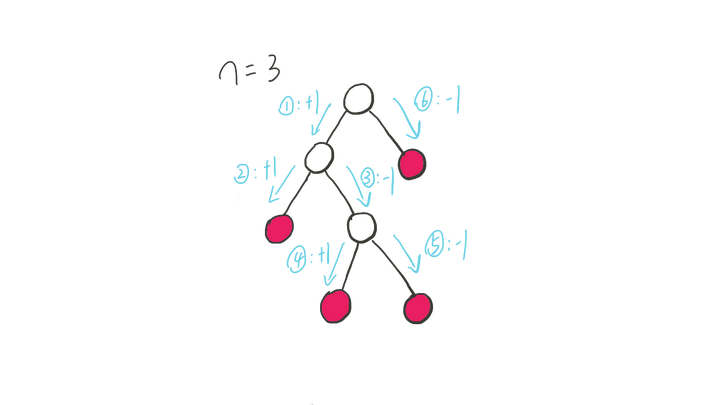
4.电影购票
电影票一张 50 coin，且售票厅没有 coin。m 个人各自持有 50 coin，n 个人各自持有 100 coin。

则有多少种排队方式，可以让每个人都买到电影票。

满足条件的01序列

题目描述：
给定 $n$ 个 $0$ 和 $n$ 个 $1$，它们将按照某种顺序排成长度为 $2n$ 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 $0$ 的个数都不少于 $1$ 的个数的序列有多少个。

输出的答案对 $10^9+7$ 取模。

输入格式：
共一行，包含整数 $n$。

输出格式：
共一行，包含一个整数，表示答案。

数据范围：
$1\le n\le 10^5$

输入样例：

3

输出样例：

5

利用卡特兰数求解

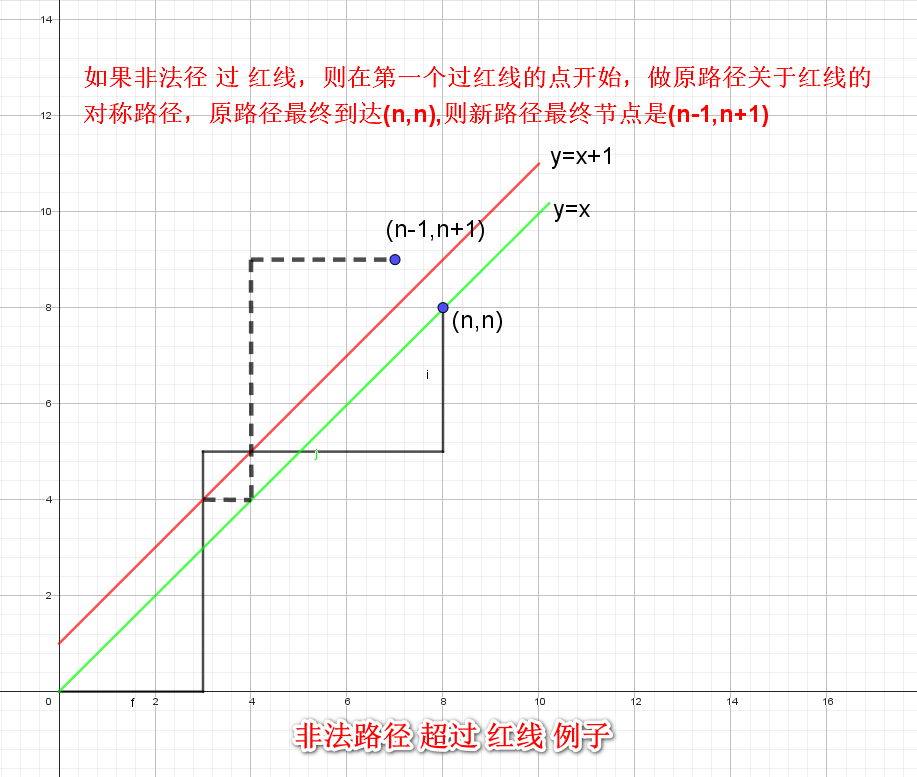
将 $1$ 和 $0$ 分别抽象为走网格图的竖走与横走，这样就把01序列的排列组合问题抽象为了路径排列组合问题。

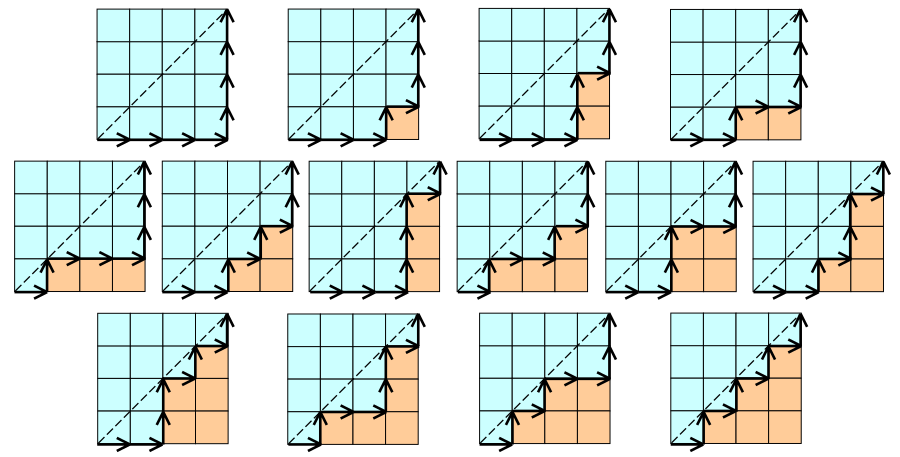
因为要满足任意前缀序列中 $0$ 的个数都不少于 $1$ 的个数，所以 $y\le x$，因为 $x$ 与 $y$ 都为正整数可进一步放缩为 $y<x+1$，所以可以抽象为在y-x坐标系上不过 $y=x+1$ 直线且上从 $(0,0)$ 到 $(3,3)$ 的路径排列组合问题。

但是由于 $C_6^3$ 表示的是所有从 $(0,0)$ 到 $(3,3)$ 的路径排列组合，包括了过 $y=x+1$ 直线的路径情况，因此要去除过 $y=x+1$ 直线抵达终点的情况。

通过对终点 $(3,3)$ 作出关于 $y=x+1$ 直线的对称点 $(2,4)$，所有从起点出发到达 $(2,4)$ 的情况可看作为过 $y=x+1$ 直线到终点的情况，即为 $C_6^2$。因此最终结果为 $C_6^3-C_6^2$，根据卡特兰数可以推出结果为 $\frac{C_6^3}{3+1}$。

代码实现

#include <iostream>
using namespace std;const int mod = 1e9 + 7;
int qmi(int a, int b, int p)
{int res = 1;while (b){if (b & 1) res = (long long)res * a % p;a = (long long)a * a % p;b >>= 1;}return res;
}
int main()
{int n;cin >> n;int a = 2 * n, b = n;int up = 1, down = 1, res = 1;for (int i = 1; i <= b; ++i){up = (long long)up * (a - i + 1) % mod;down = (long long)down * i % mod;}res = (long long)up * qmi(down, mod - 2, mod) % mod * qmi(n + 1, mod - 2, mod) % mod;cout << res << endl;return 0;
}