Problem - F - Codeforces

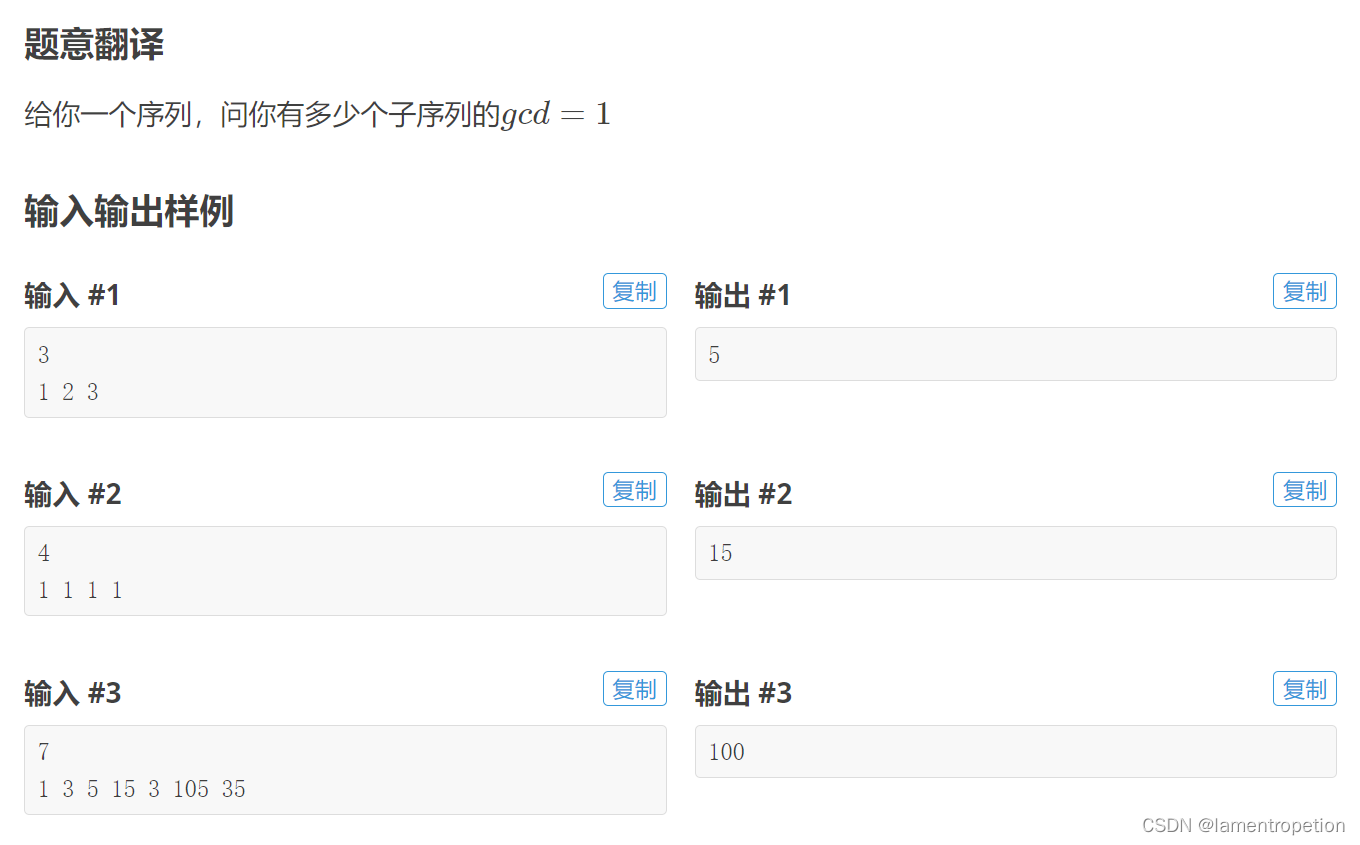
题意：

思路：

正难则反，考虑容斥

即考虑gcd != 1的所有子序列个数

因为子序列内部无序，因此不算真正的子序列，考虑枚举倍数

根据经典套路，我们去枚举 gcd，然后去枚举倍数，看以这个因子为gcd的子序列个数有多少

很显然，设该 gcd 的个数为 sum，那么每个数都有选和不选，方案数就是 (1 << sum ) - 1

但是注意到不以该因子为 gcd 的子序列会重复计算，因此需要把它们减掉

Code：

#include <bits/stdc++.h>#define int long longusing i64 = long long;constexpr int N = 1e6 + 10;
constexpr int mod = 1e9 + 7;int a[N];
int dp[N];int qpow(int a, int b, int mod) {int res = 1;while(b) {if (b & 1) {res = (res * a) % mod;}a = (a * a) % mod;b >>= 1;}return res;
}
void solve() {int n;std::cin >> n;std::map<int,int> mp;int mx = 0;for (int i = 1; i <= n; i ++) {std::cin >> a[i];mp[a[i]] ++;mx = std::max(mx, a[i]);}for (int i = mx; i >= 1; i --) {int sum = 0;for (int j = i; j <= mx; j += i) {sum += mp[j];sum %= mod;}dp[i] = ((qpow(2, sum, mod) - 1) % mod + mod) % mod;for (int j = i * 2; j <= mx; j += i) {dp[i] = ((dp[i] - dp[j]) % mod + mod) % mod;}}std::cout << dp[1] % mod<< "\n";
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t = 1;while (t--) {solve();}return 0;
}