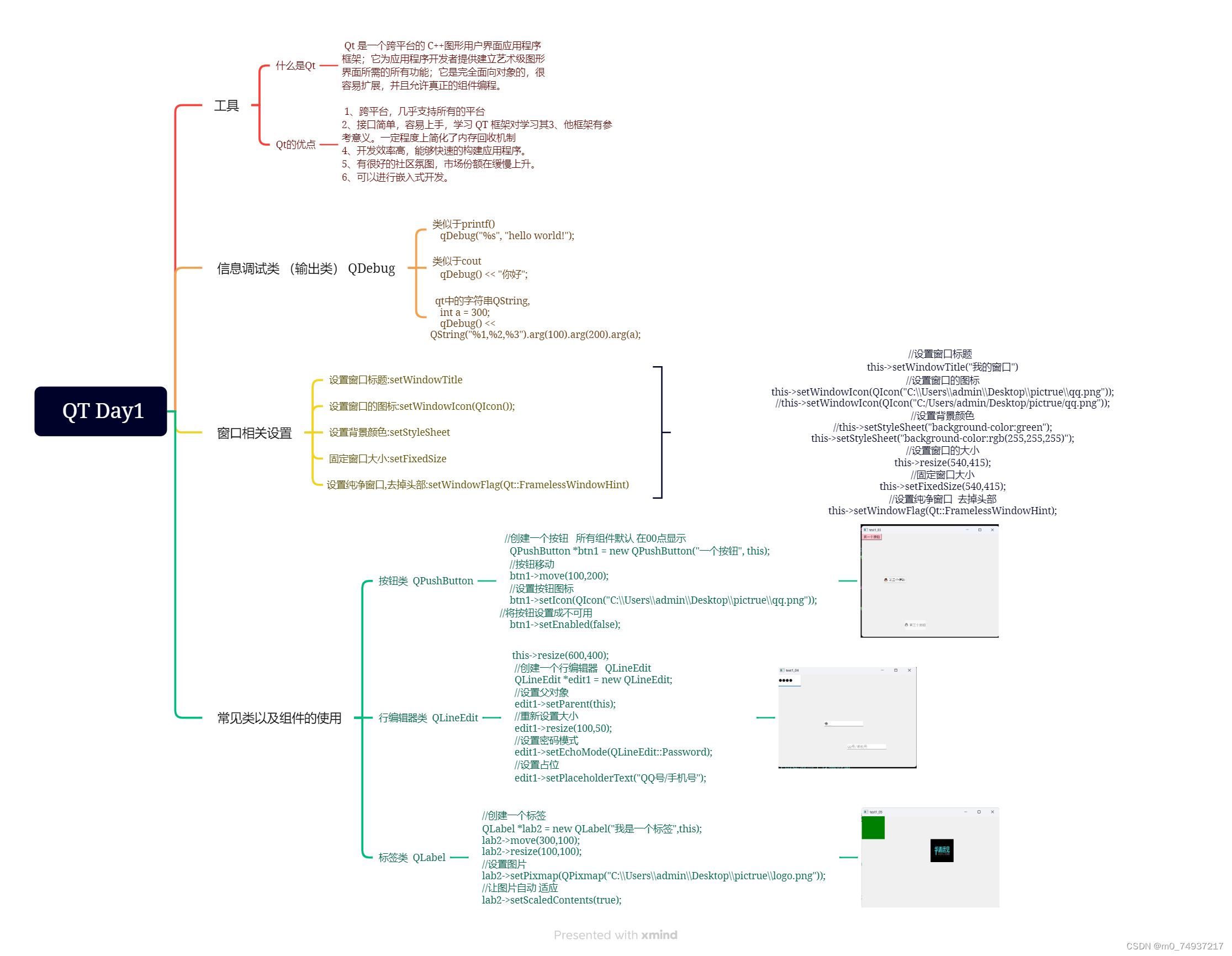
想知道如何从二维图像中如何恢复三维点，需要先知道三维点是如何映射成二维点的。

原理很简单，就是我们小学学的小孔成像原理。

为了方便我们对针孔相机模型进行数学建模，我们往往对虚拟像平面进行研究，因为虚拟像平面的方向与我们实际物体的方向一致。

根据相似三角形原理，可以得到三维坐标到二维坐标的映射：
$$P=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]⟹P^{\prime }=\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]\left(\begin{array}{c}{x}^{\prime }=f\frac{x}{z}\\ y^{\prime }=f\frac{y}{z}\end{array}\right)$$
将像平面原点坐标移动到图像的左下角：$\left(x,y,z\right)⟶\left(f\frac{x}{z}+c_x,f\frac{x}{z}+c_y\right)$

加上现实世界单位(m)到数码图片单位(pixel)的转换量：$\left(x,y,z\right)⟶\left(fk\frac{x}{z}+c_x,fk\frac{x}{z}+c_y\right)$

至此，完成了相机坐标到像平面坐标的映射：$\mathbf{P}=(\mathbf{x},\mathbf{y},\mathbf{z})⟶{\mathbf{P}}^{\prime }=\left(\alpha \frac{\mathbf{x}}{\mathbf{z}}+{\mathbf{c}}_{\mathbf{x}},\beta \frac{\mathbf{y}}{\mathbf{z}}+{\mathbf{c}}_{\mathbf{y}}\right)$​

在上面这个公式中，$z$是会改变的，因此 $P$到$P^{\prime }$并不是线性变换，我们需要引入齐次坐标，使它成为线性变换。

欧式坐标变为齐次坐标就是在最后增加一个维度，并让它的值为1：
$$(x,y)⟶\left[\begin{array}{c}x\\ y\\ 1\end{array}\right](x,y,z)⟶\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$
齐次坐标转欧式坐标：
$$\left[\begin{array}{c}x\\ y\\ w\end{array}\right]⟶(\frac{x}{w},\frac{y}{w})\left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]⟶(\frac{x}{w},\frac{y}{w},\frac{z}{w})$$
齐次坐标转到欧式坐标的结果并不是一一对应的，比如（1，1，1）和（2，2，2）转到欧式坐标都是（1，1），它们之间相差一个系数。

变为齐次坐标后$P$到$P^{\prime }$就是线性变换的，$z$的变化不会影响最后的投影结果。

由于制造工艺的原因，像平面可能不是一个矩形，所以需要引入$\theta$​进行建模：

在进行三维重建的时候往往需要用到多个相机，因此需要外参矩阵将所有点的坐标系进行统一。