微积分 --- 偏导数，方向导数与梯度(二)-编程知识

微积分 --- 偏导数，方向导数与梯度(二)

方向导数

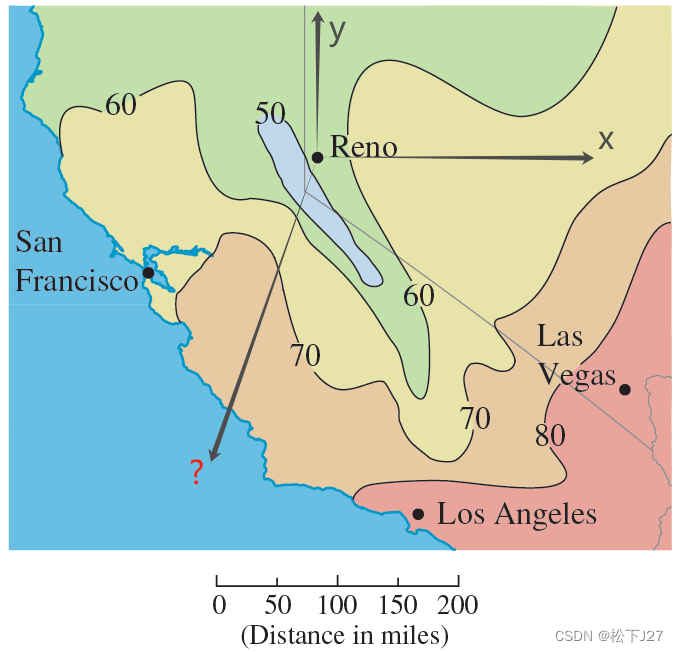
上图为一温度图，所反映的是加利福利亚洲和内华达州在十月的一天下午三点的温度。其中，图中的每一点都是温度T关于x,y的函数，即T(x,y)。对于图中的Reno市而言，沿着x方向的偏导 $T_{x}$ 反映的是温度沿着x方向，即沿着东方的变化率。沿着y方向的偏导 $T_{y}$ 反映了温度沿着北方，即y方向的变化率。这些偏导数的求法在介绍偏导数的时候都已经知道了。但如果我现在要求图中一任意方向的变化率呢，也就是图中用红色“❓”标出来的方向的变化率？

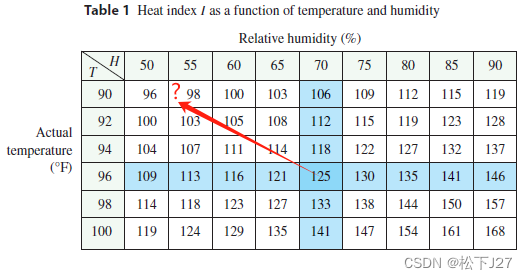
这就好比是我在偏导数中所使用的酷热指数heat index表格中，我要求温度指数在某一点处即不是沿着x也不是沿着y而是沿着指定的某一个方向的偏导该怎么求？

这就是方向导数所要解决的问题。他能让我们找到函数在某一点处沿任意方向的导数，这就是说如果原来的偏导数只能解决偏x或者偏y的问题，但方向导数能够解决即偏x也偏y的问题。可见方向导数就是函数在某一点处沿着某一方向的导数。

对上图而言，已知曲面S是二元函数z=f(x,y)在三维坐标系中的函数图像，其中z0=f(x0,y0)。点P(x0,y0,z0)为曲面S上的一点。此外，单位向量i=[1,0]表示沿x轴方向，单位向量j=[0,1]表示沿y轴方向，任意方向的单位向量u=[a,b]=ai+bj。沿方向u的垂直平面与曲面S的交线为C，该曲线上过P点的切线T的斜率即为z在方向u上的变化率，也就是函数在u方向上的导数。

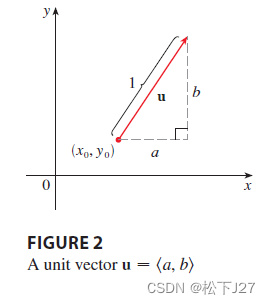
曲线C上的另一点Q(x,y,z)为，点P和Q在x-y平面上的投影为P',Q'。则向量P'Q'与单位向量u的方向相同，大小为单位向量u的h倍：

$\overrightarrow{P'Q'}=hu=[ha,hb]$

这样一来:

$x=x_{0}+ha,y=y_{0}+hb$

$z=f(x,y)=f(x_{0}+ha,y_{0}+hb)$

又：

$z_{0}=f(x_{0},y_{0})$

根据导数的定义，函数z=f(x,y)在u方向上的变化率为：

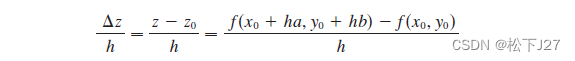
取h趋近于0的极限，得到函数在方向u上的瞬时变化率，这就是函数f在方向u上的方向导数：

若方向u与x轴正向的方向相同，则u=i=[1,0] ---》a=1,b=0，得到hu=[h,0]。代入公式得到：

$D_{i}f(x_{0},y_{0})=\lim_{h \to 0}\frac{f(x_{0}+h,y_{0})-f(x_{0},y_{0})}{h}$

若u与y轴方向相同，u=j=[0,1] ---》a=0,b=1，得到hu=[0,h]。代入公式得到：

$D_{j}f(x_{0},y_{0})=\lim_{h \to 0}\frac{f(x_{0},y_{0}+h)-f(x_{0},y_{0})}{h}$

这和直接用偏导数的计算公式算出来的一样：

这就是说，如果方向导数是一个集合的话，偏导数一定属于这个集合。或者说，偏导数是方向导数的一个特例。

此外，如果我们定义一个关于自变量h的函数g(h)：

$g(h)=f(x_{0}+ha,y_{0}+hb)$

根据导数的定义，函数在h=0处的导数为：

另一方面，我们还可以把函数g(h)用复合函数来表示:

$g(h)=f(x_{0}+ha,y_{0}+hb)\Rightarrow g(h)=f(x,y),where \; x=x_{0}+ha,y=y_{0}+hb$

根据链式求导法则有：

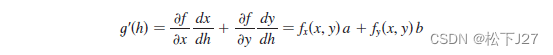
再令h=0，则有：

$x=x_{0},y=y_{0}$

最后，把4式与5式放在一起，我们有：

这个式子说明，函数f在任意方向u上的方向导数等于x方向的偏导数与一个系数的乘积与y方向的偏导数与一个系数的乘积之和。

梯度

如果我们对定理3中的公式做进一步改写，我们有：

如此一来，我们就把方向导数的公式写成了两个向量的内积或点积的形式。

如果我们暂且用▽f来表示上式中点积前面的那个向量:

则根据点积的另一种计算方法，方向导数的公式可改写为：

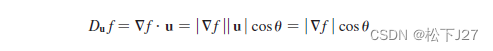
其中θ为向量▽f与向量u之间的夹角，当cosθ=1时达到最大值，此时夹角为0，u与▽f同向，方向导数的值为|▽f|。也就是，在众多个方向u中，当u转到和▽f的方向一致时，此时函数f的增加幅度最大，|▽f|非负。因为在所有的方向中，这个方向的增速最大，因此向量▽f是一个十分特殊的向量，我们称之为梯度。

这也正是深度学习中令损失函数最小化时，用到的梯度下降法中反复提及的朝着梯度相反的方向的原因。

Tips:点积的两种算法